NASA가 지금까지 화성에 착륙시킨 착륙선은 1976년 바이킹 1호부터 시작하여 2021년 2월 18일에 착륙에 성공한 Mars2020/퍼서비어런스에 이르기까지 모두 9개다. 초창기에는 무유도(unguided) 탄도 대기권 진입 방식을 사용했는데, 이는 착륙 지점의 과학적 가치를 고려하지 않고 화성에 안전하게 착륙하는 것을 목표로 한 이른바 1세대 시스템이었다. 1세대 화성 진입, 하강 및 착륙(EDL, entry, descent and landing) 시스템의 착륙 오차(landing uncertainty ellipse)는 \(150 \times 20 ~ km\) 정도로서 위험한 지형과 과학적 가치가 높은 지역에 착륙할 수 있는 능력이 없었다.

2012년 8월 게일(Gale) 크레이터에 착륙한 Mars Science Laboratory(MSL)/큐리오시티는 유도(guided) 진입 방법을 사용한 최초의 착륙선으로서 이전의 탄도형 진입 방식보다 착륙 정확도가 크게 향상되어 착륙 오차가 \(25 \times 20 ~ km\) 이었다. Mars2020에서도 유사한 유도 시스템을 사용하여 퍼서비어런스 로버를 예제로(Jezero) 크레이터 내에 성공적으로 착륙시켰다. Mars2020에서는 MSL 시스템에 지형 상대 항법 등 몇가지 새로운 기술을 도입하여 착륙 오차가 큐리오시티 보다도 작은 \(7.7 \times 6.6 ~ km\) 이었고 실제로 퍼서비어런스 로버를 목표 착륙 지점으로부터 \(2~km\) 이내에 착륙시킬 수 있었다.
화성 착륙 탐사 임무에서 진입, 하강 및 착륙(EDL) 단계는 전체 임무의 성공 여부를 직접적으로 결정하는 중요한 단계다. EDL 단계는 착륙선이 화성 대기권 경계인 고도 약 \(125 ~ km\) 에 도달하면서 시작하여 진입 단계, 하강 단계 및 착륙 단계를 거쳐 착륙선이 최종적으로 화성 표면에 도착하는 것으로 끝나는데 약 6~8분 정도 소요된다. 이와 같이 화성 EDL은 매우 짧은 시간 동안 진행되기 때문에 화성과 지구 사이가 빛의 속도로 11분 22초 정도 소요되는 거리임을 생각하면 지구에서 실시간 원격 제어를 실행하는 것은 불가능하다.

EDL의 첫 단계인 화성 대기 진입(entry) 단계는 화성 대기권의 최상층인 \(125 ~km\) 고도에서 선택한 지점인 진입 인터페이스(entry interface)에 도착하는 것으로 시작하여 초음속 낙하산을 안전하게 펼칠 수 있는 조건이 달성되는 지점에서 종료된다. 진입 단계에서는 속도가 \(4 \sim 7 ~ km/sec\) 에서 약 \(400 ~ m/sec\) 로 감소하므로 이 단계를 극초음속(hypersonic) 진입 단계라고도 한다.
지구 진입에 비해 화성 대기 진입의 어려운 점은 화성의 대기 밀도가 지구의 약 1% 에 불과하다는 것이다. 이로 인해 화성 대기 진입 단계에서 공기역학적 감속 과정이 일반적으로 매우 낮은 고도(\(10~km\) 미만)까지 비교적 오랜 시간 지속된다. 약 4분간 지속되며 초기 운동 에너지의 99%가 이 단계에서 소비된다. 따라서 이 과정에서 최대의 공기역학적 감속과 최대 발열이 발생하게 된다.

초음속 낙하산 전개 조건이 성립하면 진입 단계가 끝나고 바로 낙하산 하강 단계가 시작된다. 이 단계에서는 초기 운동에너지의 1% 정도가 소모되며 착륙선의 속도가 약 \(400 ~ m/sec\) 에서 \(60 \sim 100 ~m/sec\) 가 될 때까지 지속되는데 시간적으로는 약 2분 소요된다. 낙하산 전개 조건은 착륙선의 속도(마하수)와 동압(dynamic pressure)의 상한 및 하한으로 설정되거나 또는 화성 대기 모델을 사용한 고도와 속도에 대한 제약 조건으로 변환되어 설정된다.
낙하산 전개 위치는 하강 및 착륙 단계에서 필요한 비행 경로 수정이나 위험 감지 및 회피, 또한 착륙 지점까지 정확하게 도착할 수 있도록 착륙선의 위치, 속도 및 자세를 제어할 수 있는 충분한 시간과 공간이 확보되도록 결정해야 한다. 낙하산 전개 위치는 진입 단계의 종착 지점으로서 종착 위치 도달 정확도는 최종 착륙 정확도 요구 사항으로부터 결정할 수 있는데 MSL 에서는 종착 도달 위치 오차 범위가 약 \(10 ~ km\) 로 설정되었다.

낙하산 하강 단계가 끝나도 착륙선의 속도가 여전히 높기 때문에 마지막 동력 하강 단계가 이어지며 역추진을 이용하여 착륙 속도가 0 이 되도록 감속시킨다. 이 단계에서 소모되는 운동에너지는 전체의 0.02% 정도다. 동력 하강 단계는 약 1분 정도 진행된다. 착륙선이 지상에서 수십 미터 이내로 가까워지면 스카이크래인을 통해 로버를 하강시켜 로버의 바퀴가 지면에 닿도록 착륙시키고, 착륙선은 수백미터 밖으로 멀리 날려 보낸다. 동력 하강 단계의 주요 목표는 연착륙을 달성하기 위해 착륙선의 속도를 낮추고 적절한 착륙 장소를 선택하며 착륙 과정에서 있을지도 모르는 잠재적인 장애물을 회피하는 것이다.

이제 화성 진입 유도 (entry guidance) 알고리즘을 설계하기 위한 운동방정식을 세워보자.
화성 대기 진입 과정은 약 4분 가량 진행되므로 화성은 자전하지 않고 정지된 대기를 갖는다고 가정하면 다음과 같이 착륙선에 관한 질점(point mass) 운동방정식을 유도할 수 있다 (https://pasus.tistory.com/182).
\[ \begin{align} & \dot{r} = V \sin \gamma \tag{1} \\ \\ & \dot{V} = -\frac{D}{m} -g \sin \gamma \\ \\ & \dot{\gamma} = \frac{V \cos \gamma }{r}- \frac{g \cos \gamma}{V} + \frac{L \cos \sigma}{mV} \\ \\ & \dot{\lambda}_{lat} = \frac{V \cos \psi \cos \gamma}{r} \\ \\ & \dot{\lambda}_{lon} = \frac{V \sin \psi \cos \gamma}{r \cos \lambda_{lat} } \\ \\ & \dot{\psi} = \frac{V}{r} \tan \lambda_{lat} \sin \psi \cos \gamma + \frac{L \sin \sigma}{mV \cos \gamma} \end{align} \]
여기서 \(r\) 은 화성 중심으로부터 착륙선까지의 거리, \(V\) 는 착륙선 속력, \(\gamma\) 는 비행경로각(flight path angle)으로서 수평면과 속도벡터가 이루는 각, \(\lambda_{lat}\) 와 \(\lambda_{lon}\) 는 각각 위도와 경도, \(\psi\) 는 속도벡터의 방향각, \(m\) 은 착륙선의 질량, \(\sigma\) 는 속도벡터를 중심으로 회전한 뱅크각(bank angle)이다. 화성은 원형으로 가정하며 중력가속도는 \(g=\frac{\mu_M}{r^2}\) 으로 가정한다. \(\mu_M=42828 ~ km^3/sec^2\) 은 화성의 중력상수다.
진입 과정은 무추력으로 진행되기 때문에 식 (1)에서 착륙선의 추력은 포함되지 않았다. 착륙선의 뱅크각은 RCS(reaction control system)을 사용하여 제어할 수 있다.

항력 \(D\) 와 양력 \(L\) 은 다음과 같이 주어진다.
\[ \begin{align} & D=C_D \frac{1}{2} \rho V^2 A = \frac{q}{\beta} \tag{3} \\ \\ & L=C_L \frac{1}{2} \rho V^2 A =D \left( \frac{L}{D} \right) \\ \\ & \rho =\rho_0 e^{ -\frac{(r-R_M)}{h_s}} \end{align} \]
여기서 \(\rho\) 는 화성의 공기 밀도, \(\rho_0=0.0158 ~ kg/m^3\) 는 화성 표면에서의 공기 밀도, \(R_M=3396.2 ~ km\) 는 화성의 반지름, \(A\) 는 기준 면적, \(h_s=9.354 ~km\) 는 고도 척도, \(C_L\) 과 \(C_D\) 는 각각 양력 및 항력계수, \(\beta= \frac{m}{C_D A} \) 는 탄도계수 (ballistic coefficient), \(q=\frac{1}{2} \rho V^2\) 는 동압, \(L/D\) 는 양항비(lift-to-drag ratio)이다.
캡술 형태의 착륙선에서 양력을 발생시키기 위해서 착륙선의 질량 중심을 캡슐의 대칭축에서 의도적으로 이탈(center-of-mass offset) 시켜서 받음각(angle of attack)을 설정한다.

식 (1)에 의하면 위도와 경도에 관한 방정식을 합치면 착륙선의 운동방정식에서 세로 운동(longitudinal motion)을 가로 운동(lateral motion)으로 부터 분리할 수 있다는 것을 알 수 있다.
착륙선의 위치에서 위도와 경도의 미소(infinitesimal) 변화에 대한 위도 방향과 경도방향의 거리 변화 \(ds_{lat}\) 와 \(ds_{lon}\) 는 각각 다음과 같다.
\[ \begin{align} & ds_{lat}=r \ d\lambda_{lat} \tag{3} \\ \\ & ds_{lon}=r \cos \lambda_{lat} \ d \lambda_{lon} \end{align} \]
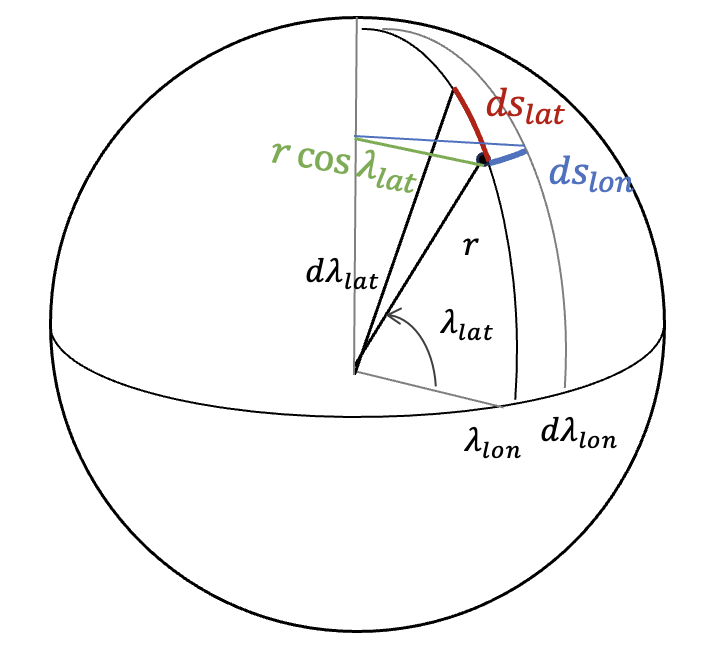
따라서 식 (1)의 위도와 경도에 관한 방정식을 이용하면 총 거리 변화율은 다음과 같이 표현할 수 있다.
\[ \begin{align} \frac{ds}{dt} &= \frac{ \sqrt{( ds_{lat} )^2+ (ds_{lon} )^2 }}{dt} \tag{4} \\ \\ & = r \sqrt{ \left( \frac{d \lambda_{lat}}{dt} \right)^2+ \cos^2 \lambda_{lat} \left( \frac{d\lambda_{lon}}{dt} \right)^2 } \\ \\ & =V \cos \gamma \end{align} \]
식 (1)에서 위도와 경도 운동방정식을 식 (4)로 대체하면 착륙선의 세로 운동방정식을 다음과 같이 쓸 수 있다.
\[ \begin{align} & \dot{h}= V \sin \gamma \tag{5} \\ \\ & \dot{V} = - \frac{D}{m} -g \sin \gamma \\ \\ & \dot{\gamma} = \frac{V \cos \gamma}{r}- \frac{g \cos \gamma}{V} + \frac{L \cos \sigma}{mV} \\ \\ & \dot{s} = V \cos \gamma \end{align} \]
여기서 \(h=r-R_M\) 는 착륙선의 고도, \(s\) 는 수평 거리(horizontal distance)다. \(\dot{s}\) 는 수평방향의 접선 속력이므로 식 (5)의 마지막 식을 다음과 같이 쓰기도 한다.
\[ \begin{align} \dot{\Lambda} = - \frac{V \cos \gamma}{r} \tag{6} \end{align} \]
여기서 \(\Lambda\) 는 화성 중심을 기준으로 한 착륙선의 현재 위치와 진입 종료 지점의 사잇각으로서 지상거리(ground distance) 또는 잔여거리(range-to-go)라고 한다. 잔여거리는 각도 단위이다. 진입 인터페이스 위치가 아니라 진입 종료 위치에 대한 각이므로 식 (6)에서 음의 부호(마이너스)가 붙었다.

착륙선이 이동한 수평 거리를 다운레인지(downrange)라고 하고, 착륙선과 원래 목표로 한 궤적 사이의 거리를 크로스레인지(crossrange)라고 한다.
아래 그림과 게시글 (https://pasus.tistory.com/319)의 식 (13)에 의하면 화성 지표면을 기준으로 한 다운레인지 \(S_D\) 는 다음과 같이 계산할 수 있다. 그림에서 빨간색은 기준 궤적이고 \(\Delta \psi\) 는 기준 궤적과 실제 궤적의 방향각 차이다.

\[ \begin{align} S_D &= R_M \Lambda \tag{7} \\ \\ &= R_M \cos^{-1} \left( \sin \lambda_{lat,t} \sin \lambda_{lat} + \cos \lambda_{lat,t} \cos \lambda_{lat} \cos ( \lambda_{lon,t}-\lambda_{lon} ) \right) \end{align} \]
또한 게시글 (https://pasus.tistory.com/319)의 식 (9)에서 \( C \to \frac{\pi}{2}\), \(c \to \Lambda\), \(B \to \Delta \psi\), \(b\) 를 크로스레인지 각으로 놓으면 화성 지표면을 기준으로 한 크로스레인지 \(S_C\)는 다음과 같이 계산할 수 있다.
\[ \begin{align} S_C &=R_M b \tag{8} \\ \\ &= R_M \sin^{-1} \left( \sin \Delta \psi \sin \Lambda \right) \end{align} \]
'유도항법제어 > 유도항법' 카테고리의 다른 글
| 두빈스 경로 (Dubins Path) - 2 (0) | 2024.05.25 |
|---|---|
| 두빈스 경로 (Dubins Path) - 1 (0) | 2024.05.25 |
| [INS] 관성항법시스템 오차 방정식 (INS Error Equations) (0) | 2024.03.15 |
| [INS] 관성항법 방정식 (Kinematics of Inertial Navigation) (0) | 2024.03.03 |
| 최적유도법칙과 비례항법유도 (PNG) (0) | 2023.09.20 |




댓글