평면상에서 시작점과 끝점을 연결하는 최단거리 경로를 구하려고 한다. 단 시작점과 끝점에서 각각 출발 방향과 도착 방향이 정해져 있고 경로가 가질 수 있는 최대 곡률(curvature)에 제한이 있는 경우다.
이 문제는 제약조건이 있는 최적화 문제로서 최단거리 경로는 최대 곡률을 갖는 원형 호와 직선을 결합하여 만들어진다는 것이 증명되었다. 이 최단거리 경로를 두빈스 경로 (Dubins path)라고 한다. 두빈스 경로는 기하학적인 방법으로 간단히 생성할 수 있기 때문에 이동 로봇, 드론, 무인 잠수정 등의 운동체 경로 계획 방법으로 널리 사용되고 있다.
두빈스 경로는 CSC 또는 CCC 경로 중 하나다. 여기서 C는 원호(circular arc), S는 직선(straight line)을 나타낸다. CCC 경로는 서로 접하는 세 개의 연속된 원호로 구성되며, CSC는 직선과 두 개의 원호로 구성된다. 이 때 원호의 반경은 주어진 최대 곡률 제약 조건에 해당하는 운동체의 최소 회전 반경과 동일하게 선택된다. CCC 경로는 두 지점 사이의 거리가 가까운 경우에만 선택되기 때문에 여기서는 제외하고 CSC 경로에 대해서만 논하기로 한다.
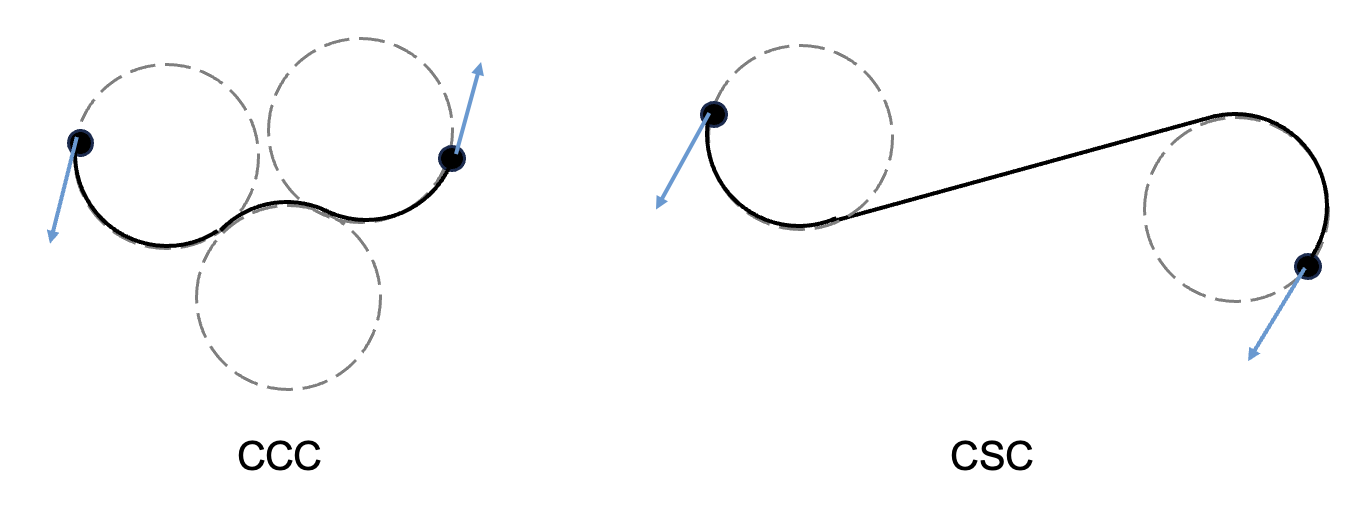
CSC는 RSR, LSL, RSL, LSR 등 네 가지로 구성된다. 여기서 R은 우회전(right turn), L은 좌회전(left turn), S는 직진을 나타낸다. 최단 경로는 이 네 가지 경로를 따라 거리를 비교하여 선택한다.

일반적으로 x-y 평면상에서 두빈스 경로를 설계하나 여기서는 향후 확장성을 고려하여 3차원 공간상에 있는 임의의 평면에서 경로를 설계해 보고자 한다.
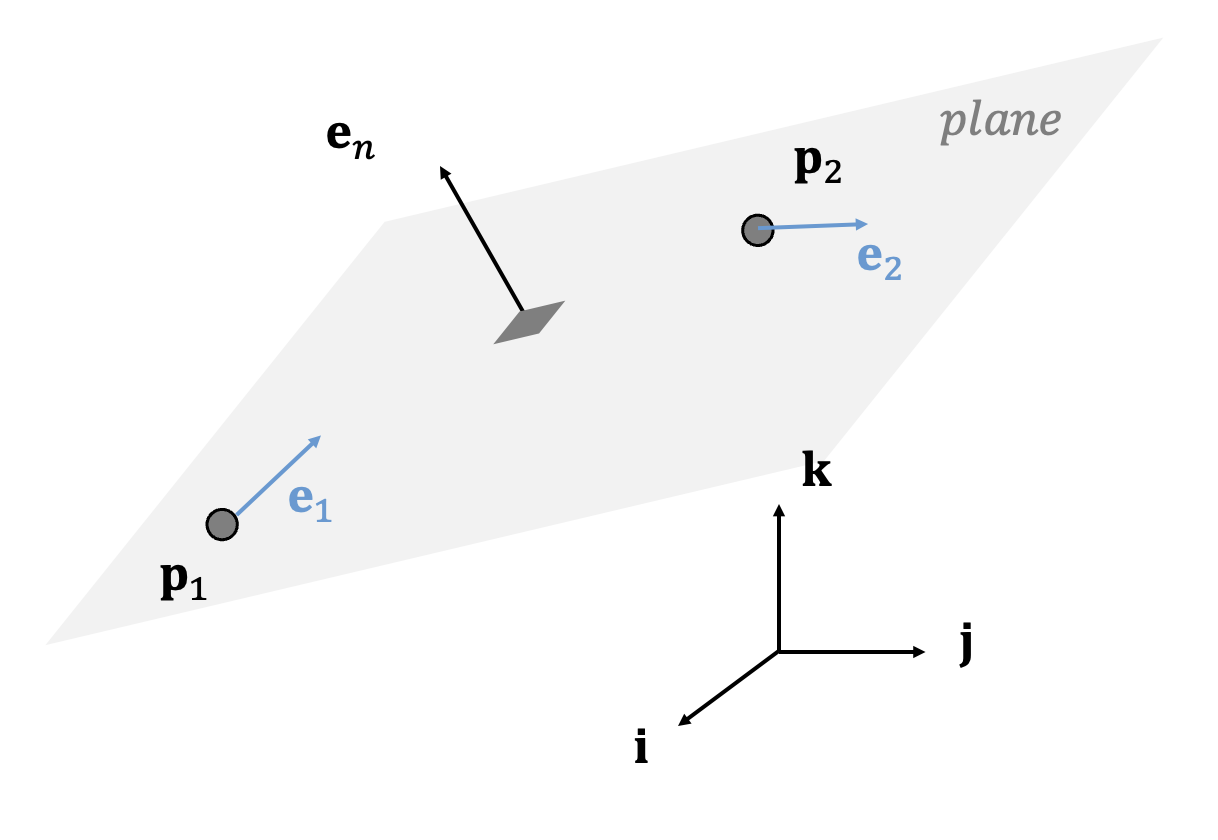
평면상에서 두빈스 경로의 네 가지 경로는 시작점 \(\mathbf{p}_1\) 과 끝점 \(\mathbf{p}_2\), 그리고 시작점에서의 방향을 나타내는 단위벡터(또는 방향벡터) \(\mathbf{e}_1\) 과 끝점에서의 방향벡터 \(\mathbf{e}_2\) 로 설계할 수 있다. 단, 여기서 벡터 \((\mathbf{p}_2 -\mathbf{p}_1)\) 과 방향벡터 \(\mathbf{e}_1\) 과 \(\mathbf{e}_2\) 는 같은 평면상에 존재해야 한다. 아래 그림에서 \(\mathbf{e}_n\) 은 평면에 수직인 단위벡터이다.
주어진 시작점과 방향벡터에서 아래 그림과 같이 왼쪽과 오른쪽으로 접하는 두 원이 있다. 이 원의 반지름은 운동체의 최소 회전 반경 (또는 최대 곡률) \(R\) 이다. 운동체는 왼쪽 또는 오른쪽으로 회전하여 원의 회전 방향으로 이 원호를 통과할 수 있다. 왼쪽과 오른쪽의 구분은 운동체의 운동 방향을 기준으로 한다.
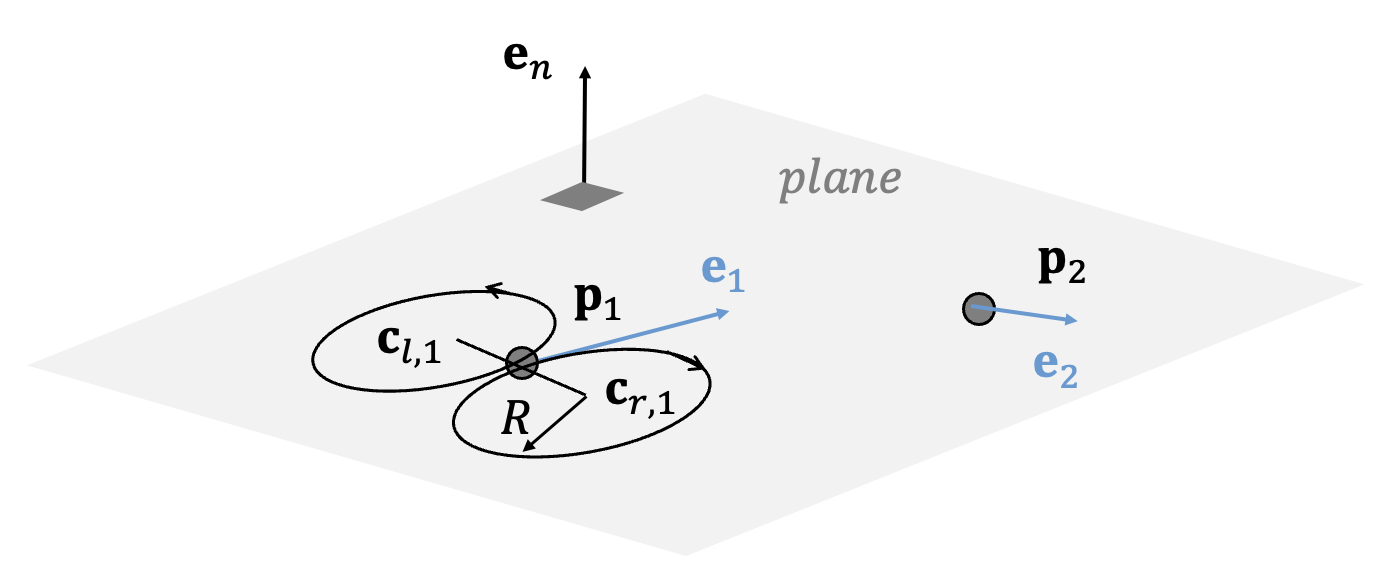
두 원의 중심점은 시작점에서의 방향벡터가 두 원에 접하도록 다음과 같이 계산할 수 있다.
\[ \begin{align} \mathbf{c}_{l,1} &= \mathbf{p}_1+R \ \mathbf{e}_n \times \mathbf{e}_1 \tag{1} \\ \\ \mathbf{c}_{r,1} &= \mathbf{p}_1-R \ \mathbf{e}_n \times \mathbf{e}_1 \end{align} \]
여기서 \(\mathbf{c}_{l,1}\) 은 시작점에 접한 왼쪽 원 중심점, \(\mathbf{c}_{r,1}\) 은 오른쪽 원 중심점이다. 끝점에서 각각 왼쪽과 오른쪽으로 접하는 두 원의 중심점도 같은 방법으로 계산할 수 있다.
\[ \begin{align} \mathbf{c}_{l,2} &= \mathbf{p}_2+R \ \mathbf{e}_n \times \mathbf{e}_2 \tag{2} \\ \\ \mathbf{c}_{r,2} &= \mathbf{p}_2-R \ \mathbf{e}_n \times \mathbf{e}_2 \end{align} \]
4개 원의 중심점을 구하는 매트랩(Matlab) 코드는 다음과 같다.
function [left_c1,right_c1,left_c2,right_c2] ...
= circle_with_R(p1,p2,e1,e2,R,en)
% input: two positions p1, p2 (vectors) and directions e1, e2
% % circle radius R, normal vector to plane en
% output: centers of four circles
% left_circle at p1, right circle at p1
% left circle at p2, right circle at p2
%
% calculate the centers of the left and right circles at p1
% 'left' means 'rotation axis is the same to plane normal vector'
left_c1 = p1 + R * cross(en, e1);
right_c1 = p1 - R * cross(en, e1);
% calculate the centers of the left and right circles at p2
left_c2 = p2 + R * cross(en, e2);
right_c2 = p2 - R * cross(en, e2);
end
RSR 경로는 시작점 \(\mathbf{p}_1\) 에서 오른쪽 원을 타고 우회전한 다음 직진하고 끝점 \(\mathbf{p}_2\) 에서 오른쪽에 접한 원에서 다시 우회전하여 끝점에 도착하는 것으로 구성된다. 아래 그림에는 원호에서 직선으로의 전환점인 풀아웃(pull-out) 지점 \(\mathbf{q}_1\) 과 직선에서 원호로 전환점인 휠오버(wheel-over) 지점 \(\mathbf{q}_2\) 와 이를 연결하는 직선을 각각 보여준다.
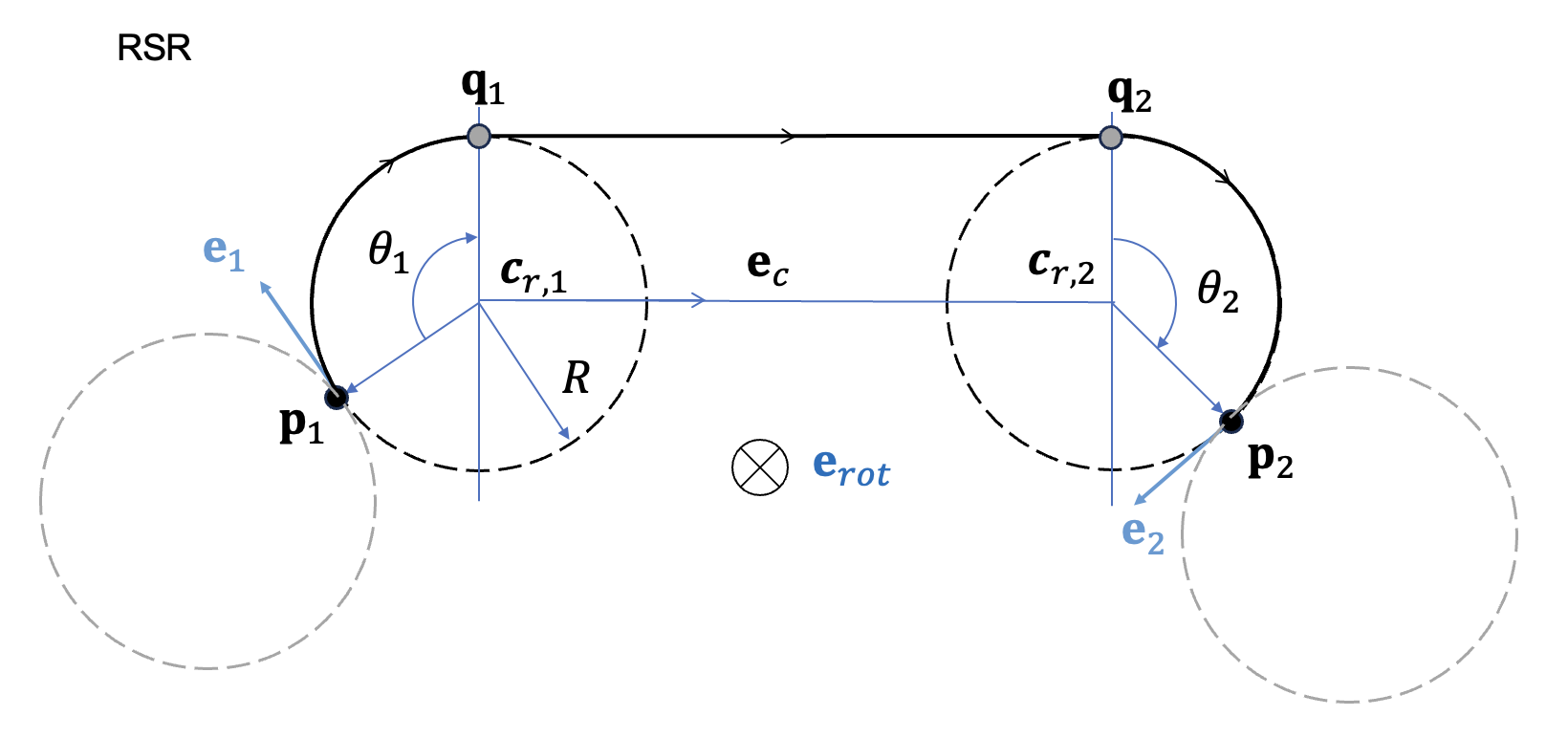
풀아웃 지점 \(\mathbf{q}_1\) 과 휠오버 지점 \(\mathbf{q}_2\) 는 다음과 같이 계산할 수 있다.
\[ \begin{align} \mathbf{q}_1 &= \mathbf{c}_1-R \ \mathbf{e}_{rot} \times \mathbf{e}_c \tag{3} \\ \\ \mathbf{q}_2 &= \mathbf{c}_2-R \ \mathbf{e}_{rot} \times \mathbf{e}_c \end{align} \]
여기서 \(\mathbf{e}_{rot}=-\mathbf{e}_n\) 으로서 오른쪽 원호의 회전방향을 나타내고, \(\mathbf{e}_c\) 는 두 원의 중심점인 \(\mathbf{c}_1= \mathbf{c}_{r,1}\) 에서 \(\mathbf{c}_2= \mathbf{c}_{r,2}\) 로 향하는 단위벡터로서 다음과 같이 주어진다.
\[ \begin{align} \mathbf{e}_c= \frac{\mathbf{c}_2- \mathbf{c}_1}{‖\mathbf{c}_2- \mathbf{c}_1‖_2} \tag{4} \end{align} \]
두 지점 \(\mathbf{p}_1\) 에서 \(\mathbf{q}_1\) 까지 이동하는 회전 각도 \(\theta_1\) 은 다음과 같이 계산할 수 있다.
\[ \begin{align} & \phi_1= \cos^{-1} \left( \frac{(\mathbf{p}_1-\mathbf{c}_1 ) \cdot (\mathbf{q}_1- \mathbf{c}_1 )}{R^2} \right) \tag{5} \\ \\ & \theta_1= \begin{cases} \phi_1, & \mbox{if } \mathbf{e}_1 \cdot \mathbf{e}_{d1} \ge 0 \\ 2\pi- \phi_1, & \mbox{else } \end{cases} \end{align} \]
여기서 \(\mathbf{e}_d1\) 은 \(\mathbf{p}_1\) 에서 \(\mathbf{q}_1\) 로 향하는 단위벡터다.
\[ \begin{align} \mathbf{e}_{d1}= \frac{ \mathbf{q}_1-\mathbf{p}_1}{‖\mathbf{q}_1-\mathbf{p}_1 ‖_2} \tag{6} \end{align} \]
비슷한 방법으로 \(\mathbf{q}_2\) 에서 \(\mathbf{p}_2\) 까지 이동하는 회전 각도 \(\theta_2\) 는 다음과 같이 계산할 수 있다.
\[ \begin{align} & \phi_2= \cos^{-1} \left( \frac{(\mathbf{p}_2-\mathbf{c}_2 ) \cdot (\mathbf{q}_2- \mathbf{c}_2 )}{R^2} \right) \tag{7} \\ \\ & \theta_2= \begin{cases} \phi_2, & \mbox{if } \mathbf{e}_2 \cdot \mathbf{e}_{d2} \ge 0 \\ 2\pi- \phi_2, & \mbox{else } \end{cases} \end{align} \]
여기서 \(\mathbf{e}_{d2}\) 는 \(\mathbf{q}_2\) 에서 \(\mathbf{p}_2\) 로 향하는 단위벡터다.
\[ \begin{align} \mathbf{e}_{d2}= \frac{ \mathbf{p}_2-\mathbf{q}_2}{‖\mathbf{p}_2-\mathbf{q}_2 ‖_2} \tag{8} \end{align} \]
LSL 경로는 시작점 \(\mathbf{p}_1\) 에서 왼쪽 원을 타고 좌회전한 다음 직진하고 끝점 \(\mathbf{p}_2\) 에서 왼쪽에 접한 원에서 다시 좌회전하여 끝점에 도착하는 것으로 구성된다. 아래 그림에는 원호에서 직선으로의 전환점인 풀아웃(pull-out) 지점 \(\mathbf{q}_1\) 과 직선에서 원호로 전환점인 휠오버(wheel-over) 지점 \(\mathbf{q}_2\) 와 이를 연결하는 직선을 각각 보여준다.
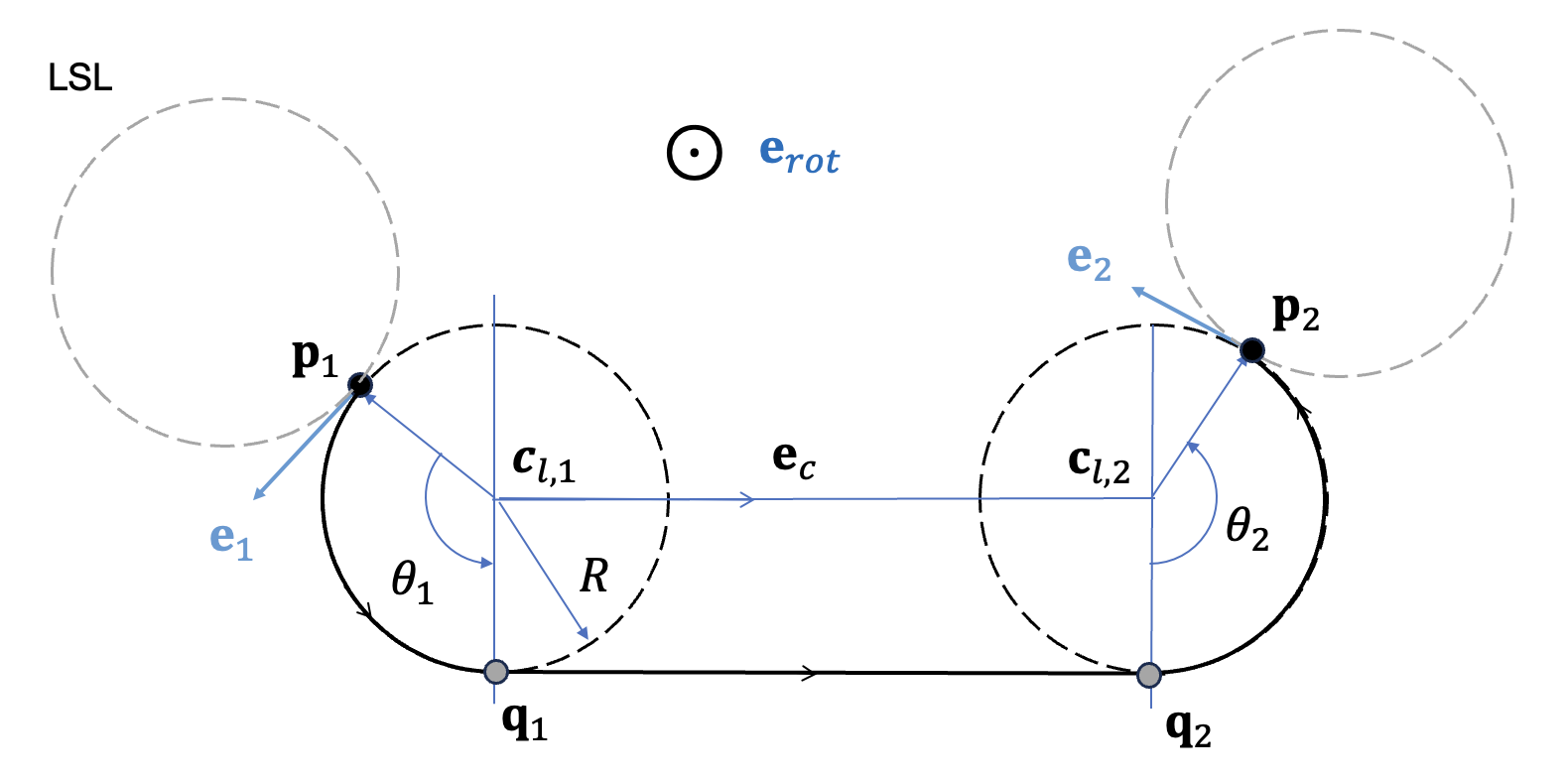
풀아웃 \(\mathbf{q}_1\), 휠오버 지점 \(\mathbf{q}_2\) 및 회전 각도 \(\theta_1, \ \theta_2\) 는 다음과 같이 치환하면 RSR의 경로와 동일한 방정식 (3)\(\sim\)(8)로 계산할 수 있다.
\[ \begin{align} & \mathbf{e}_{rot}= \mathbf{e}_n \tag{9} \\ \\ & \mathbf{c}_1= \mathbf{c}_{l,1} \\ \\ & \mathbf{c}_2= \mathbf{c}_{l,2} \end{align} \]
RSR와 LSL의 경로를 따르는 두 지점 \(\mathbf{p}_1\) 과 \(\mathbf{p}_2\) 사이의 거리 \(s_f\) 는 원호의 길이와 직선의 길이를 합산하여 계산한다.
\[ \begin{align} s_f=R \theta_1+ ‖ \mathbf{q}_2- \mathbf{q}_1 ‖_2+R \theta_2 \tag{10} \end{align} \]
RSR과 LSL 경로의 풀아웃 \(\mathbf{q}_1\), 휠오버 \(\mathbf{q}_2\) 및 회전 각도 \(\theta_1, \ \theta_2\) 와 시작점 \(\mathbf{p}_1\) 에서 끝점 \(\mathbf{p}_2\) 까지의 이동 거리를 구하는 매트랩 코드는 다음과 같다.
% RSR --------------------------------------------
function param = RSR(right_c1, right_c2, p1, p2, e1, e2, R, en)
c1 = right_c1;
c2 = right_c2;
e_rot = -en; % right circle rotation axis
[dist, q1, q2, the1, the2] = oneSone(c1, c2, p1, p2, e1, e2, R, e_rot);
param.dist = dist;
param.q1 = q1;
param.q2 = q2;
param.c1 = c1;
param.c2 = c2;
param.the1 = the1;
param.the2 = the2;
param.rot1 = e_rot;
param.rot2 = e_rot;
end
% LSL --------------------------------------------
function param = LSL(left_c1, left_c2, p1, p2, e1, e2, R, en)
c1 = left_c1;
c2 = left_c2;
e_rot = en; % left circle rotation axis
[dist, q1, q2, the1, the2] = oneSone(c1, c2, p1, p2, e1, e2, R, e_rot);
param.dist = dist;
param.q1 = q1;
param.q2 = q2;
param.c1 = c1;
param.c2 = c2;
param.the1 = the1;
param.the2 = the2;
param.rot1 = e_rot;
param.rot2 = e_rot;
end
% common code in RSR and LSL --------------------------
function [dist, q1, q2, theta1, theta2] = oneSone(c1, c2, p1, p2, e1, e2, R, e_rot)
e_c = (c2-c1)/norm(c2-c1);
q1 = c1 - R*cross(e_rot,e_c);
e_d1 = (q1-p1)/norm(q1-p1);
q2 = c2 - R*cross(e_rot,e_c);
e_d2 = (p2-q2)/norm(p2-q2);
theta1 = acos((p1-c1)'*(q1-c1)/R^2);
if e1'*e_d1 < 0
theta1 = 2*pi - theta1;
end
theta2 = acos((p2-c2)'*(q2-c2)/R^2);
if e2'*e_d2 < 0
theta2 = 2*pi - theta2;
end
dist = R*theta1 + norm(q2-q1) + R*theta2;
end
'유도항법제어 > 유도항법' 카테고리의 다른 글
| 동차 좌표 (Homogeneous Coordinates) (0) | 2026.01.29 |
|---|---|
| 두빈스 경로 (Dubins Path) - 2 (0) | 2024.05.25 |
| 화성 착륙 과정과 진입 운동방정식 (0) | 2024.04.28 |
| [INS] 관성항법시스템 오차 방정식 (INS Error Equations) (0) | 2024.03.15 |
| [INS] 관성항법 방정식 (Kinematics of Inertial Navigation) (0) | 2024.03.03 |




댓글