제약조건이 있는 비선형 다변수 함수 \( f(\mathbf{x}) \)의 최소값 (또는 최대값)을 구하는 문제를 정적 최적화(static optimization) 문제 또는 비선형 프로그래밍 문제(NLP, nonlinear programming problem)라고 한다. 수식으로 표현하면 다음과 같다.
\[ \begin{align} & p^* = \min_{\mathbf{x}} f(\mathbf{x}) \\ \\ subject \ to \ \ \ & g_i (\mathbf{x}) \le 0, \ \ \ i=1,...,m \\ \\ & h_j (\mathbf{x}) = 0, \ \ \ j=1,...,p \end{align} \]
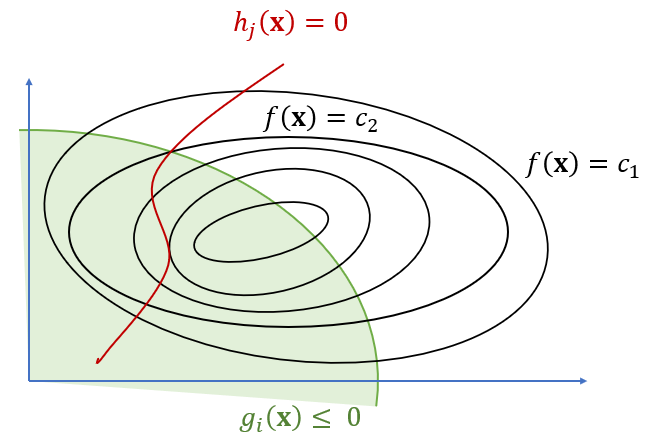
여기서 \( \mathbf{x} \in R^n \)을 최적화 변수(optimization variable)라고 하고, \( f(\mathbf{x}):R^n \to R \) 을 목적함수(objective function), \( g_i (\mathbf{x}):R^n \to R \) 을 부등식 제약함수(inequality constraint function), \( h_j (\mathbf{x}):R^n \to R \) 을 등식 제약함수(equality constraint function)라고 한다. 부등식, 등식 제약함수는 편의상 다음과 같이 벡터 형태로 표현하기도 한다.
\[ \begin{align} \mathbf{g} (\mathbf{x}) & \le 0 \\ \\ \mathbf{h}(\mathbf{x}) &= 0 \end{align} \]
여기서 부등식과 등식은 벡터 함수 \( \mathbf{g}(\mathbf{x}), \mathbf{h}(\mathbf{x}) \)의 성분별로 적용된다.
만약 제약조건을 만족하는 \( \mathbf{x} \)값이 존재하지 않는다면 최적화 문제는 실현불가능(infeasible)이라고 하고 그 때의 최소값은 \( p^* = \infty \)가 된다.
비선형 다변수 함수 \( f(\mathbf{x}) \)의 최대값을 구하는 문제는 \( -f(\mathbf{x}) \)의 최소값을 구하는 문제와 같으므로 최적화 문제를 최소화와 최대화 문제로 따로 구별할 필요는 없다.
만약 목적함수와 부등식 제약함수가 컨벡스(convex) 함수이고 등식 제약함수가 어파인(affine) 함수로 주어진다면, 이 최적화 문제를 컨벡스 최적화 문제(convex optimization problem)라고 한다. 즉 컨벡스 최적화 문제는 다음과 같다.
\[ \begin{align} & p^* = \min_{\mathbf{x}} f(\mathbf{x}) \\ \\ subject \ to \ \ \ & g_i (\mathbf{x}) \le 0, \ \ \ i=1,...,m \\ \\ & A \mathbf{x} = \mathbf{b} \end{align} \]
여기서 \( f(\mathbf{x}) \)와 \( g_i (\mathbf{x}),i=1,…,m \) 는 컨벡스 함수이고 \( A \)는 \( p \times n \) 행렬, \( \mathbf{b} \)는 \( p \times 1 \) 벡터이다.
만약 목적함수와 부등식 제약함수, 등식 제약함수가 모두 어파인(affine) 함수로 주어진다면, 이 최적화 문제를 선형 프로그래밍(LP, linear programming)문제라고 한다. 즉 LP 문제는 다음과 같다.
\[ \begin{align} & p^* = \min_{\mathbf{x}} \mathbf{c}^T \mathbf{x} + \mathbf{d} \\ \\ subject \ to \ \ \ & G \mathbf{x} \le \mathbf{z} \\ \\ & A \mathbf{x} = \mathbf{b} \end{align} \]
여기서 \( G \)는 \( m \times n \) 행렬, \( \mathbf{z} \)는 \( m \times 1 \) 벡터, \( A \)는 \( p \times n \) 행렬, \( \mathbf{b} \)는 \( p \times 1 \) 벡터이다. LP는 다면체(polyhedron) 상에서 어파인 함수를 최소화하는 문제다.

만약 목적함수가 2차함수이고, 부등식 제약함수와 등식 제약함수가 어파인(affine) 함수로 주어진다면, 이 최적화 문제를 2차 프로그래밍(QP, quadratic programming)문제라고 한다. 즉 QP 문제는 다음과 같다.
\[ \begin{align} & p^* = \min_{\mathbf{x}} \frac{1}{2} \mathbf{x}^T P \mathbf{x} + \mathbf{c}^T \mathbf{x} + \mathbf{d} \\ \\ subject \ to \ \ \ & G \mathbf{x} \le \mathbf{z} \\ \\ & A \mathbf{x} = \mathbf{b} \end{align} \]
여기서 \( P \)는 \( n \times n \) 행렬, \( G \)는 \( m \times n \) 행렬, \( \mathbf{z} \)는 \( m \times 1 \) 벡터, \( A \)는 \( p \times n \) 행렬, \( \mathbf{b} \)는 \( p \times 1 \) 벡터이다. \(P \ge 0\) 이면 목적함수가 컨벡스 함수이므로 QP는 컨벡스 문제가 된다. QP는 다면체 상에서 컨벡스 2차함수를 최소화하는 문제다.

'AI 수학 > 최적화' 카테고리의 다른 글
| 라그랑지 곱수법 (0) | 2020.10.01 |
|---|---|
| 경사하강법 (0) | 2020.09.30 |
| 스칼라 함수를 벡터로 두번 미분하기 : 헤시안 (1) | 2020.07.17 |
| 벡터 함수를 벡터로 미분하기 : 자코비안 (0) | 2020.07.16 |
| 스칼라 함수를 벡터로 미분하기 : 그래디언트 (0) | 2020.07.16 |




댓글