[PSOC-12] 예제 : 램버트 문제 (Lambert’s problem)

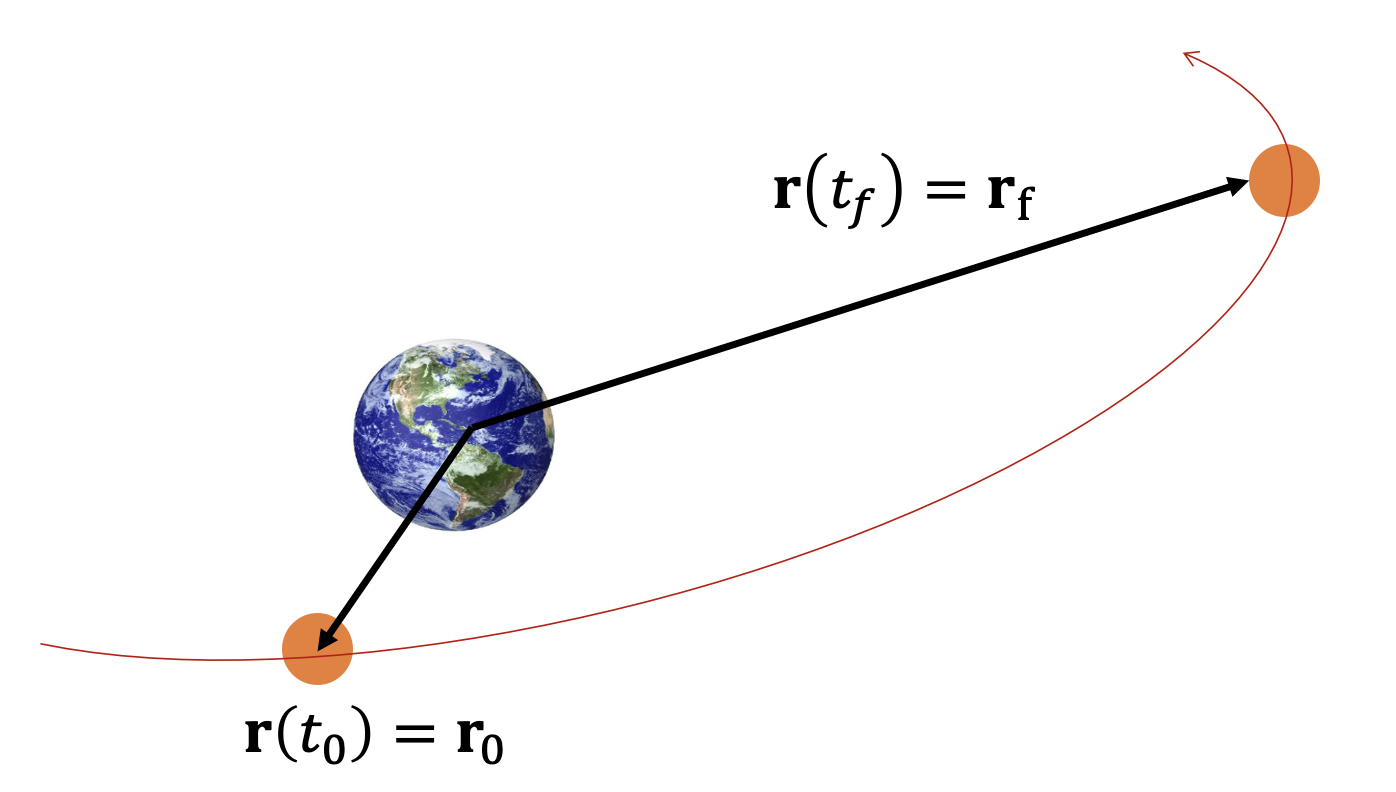
램버트 문제(Lambert's problem)는 이체문제(two-body problem)에서 유도된 기본 궤도 미분 방정식에 대한 2점 경계값 문제(TPBVP, two-point boundary value problem)이다.

$\begin{aligned} (1) & \frac{d^{2} r}{d t^{2}} + \frac{μ}{(\sqrt{r \cdot r})^{3}} r = 0 \\ r (t_{0}) = r_{0}, r (t_{f}) = r_{f}, t_{0}, t_{f} given \end{aligned}$

여기서 $μ$ 는 중력 파라미터, $r$ 은 관성좌표계의 원점에서 질점까지의 위치벡터다.

램버트 문제의 솔루션은 여러가지가 제안되어 있지만 여기서는 램버트 문제를 최적제어 문제로 변환시킨 후 로바토 유사 스펙트럴 방법(LPM)으로 풀어보고자 한다 (https://pasus.tistory.com/282).

램버트 문제를 최적제어 문제로 변환하면 다음과 같다 (https://pasus.tistory.com/268).

$\begin{aligned} (2) & \arg min_{v} J & = \int_{t_{0}}^{t_{f}} (\frac{1}{2} v \cdot v + \frac{μ}{\sqrt{r \cdot r}}) d t \\ (3) & subject to : & \frac{d r}{d t} = v \\ (4) & r (t_{0}) = r_{0}, r (t_{f}) = r_{f} \end{aligned}$

이 예제에서는 다음 수치를 사용한다.

$\begin{aligned} r_{0} = {[\begin{array}{c} 5, 000 & 10, 000 & 2, 100 \end{array}]}^{T} k m \\ r_{f} = {[\begin{array}{c} - 14, 600 & 2, 500 & 7, 000 \end{array}]}^{T} k m \\ t_{f} - t_{0} = 3, 600 s e c (1 h r) \\ μ = 398, 600 k m^{3} / s^{2} \\ R = 6, 378 k m (Earth radius) \end{aligned}$

그러면 구하고자 하는 램버트 문제의 정답은 다음과 같다.

$\begin{aligned} v_{0} = {[\begin{array}{c} - 5.99249 & 1.92536 & 3.24564 \end{array}]}^{T} k m / s \\ v_{f} = {[\begin{array}{c} - 3.31246 & - 4.19662 & - 0.38529 \end{array}]}^{T} k m / s \end{aligned}$

과연 어느 정도의 정확도로 LPM이 답을 계산하는지 알아보도록 하자.

먼저 본 예제에서 사용하는 거리와 속도, 시간의 단위를 그대로 최적화에 사용하기에는 수치의 범위가 너무 크므로 천문단위를 이용하여 무차원화 시킨다 (https://pasus.tistory.com/183).

% parameters
mu_orig=398600; % mu=GM
DU=6378;
TU=DU^(3/2)/sqrt(mu_orig);
DUTU=DU/TU;

mu=1;
t0=0;

% problem formulation
tf_orig=60*60;

rr0_0=[5000 10000  2100]';
rrf_0=[-14600  2500  7000]';

rr0 = rr0_0/DU;
rrf = rrf_0/DU;
tf = tf_orig/TU;

여기서는 $N = 12$ 개의 LGL 콜로케이션 포인트를 사용한다. LGL 콜로케이션 포인트와 보간점, LGL 쿼드래처 포인트의 가중치(weighting) $w_{j}$ , 미분행렬 $D_{j i}$ 를 다음과 같이 계산한다.

% parameters for pseudospectral
N=12;  % number of collocation points
points=GaussPoints(N,'LGL'); % LGL collocation points (N)
col_point=points';
int_point=col_point; % interpolating points (N)
Dji=LagrangePolyDerivative(col_point,int_point); % Differentiation matrix
gweights=GaussianQuadrature(N,'LGL'); % LGL quadrature weights

LPM에서는 상태변수 $r (τ)$ 와 제어변수 $v (τ)$ 를 $(N - 1)$ 차 라그랑지 다항식으로 근사화한다.

$\begin{aligned} r (τ) \approx \sum_{i = 1}^{N} R_{i} L_{i} (τ) \\ v (τ) \approx \sum_{i = 1}^{N} V_{i} L_{i} (τ) \end{aligned}$

목적함수 (2)는 다음과 같이 $N$ 개의 LGL 포인트를 이용한 가우시안 쿼드래처로 근사화 된다.

$J = \frac{(t_{f} - t_{0})}{2} \sum_{j = 1}^{N} w_{j} (\frac{1}{2} V_{j}^{T} V_{j} + \frac{μ}{\sqrt{R_{j}^{T} R_{j}}})$

rsum=0;
for ii=1:N
    rsum=rsum+ww(ii)/sqrt(rr(ii,1)*rr(ii,1)+ ...
         rr(ii,2)*rr(ii,2)+rr(ii,3)*rr(ii,3)+ep);
end

vsum=(ww.*vv(:,1))'*vv(:,1)+(ww.*vv(:,2))'*vv(:,2)+(ww.*vv(:,3))'*vv(:,3);
rcost = (tf-t0)/2*((0.5*vsum)+mu*rsum);

식 (4)의 경계조건은 다음과 같다.

$\begin{aligned} R_{1} - r_{0} = 0 \\ R_{N} - r_{f} = 0 \end{aligned}$

% equality constraints
ceq = [rr(1,1)-param.rr0(1); 
       rr(1,2)-param.rr0(2); 
       rr(1,3)-param.rr0(3); 
       rr(Nitp,1)-param.rrf(1); 
       rr(Nitp,2)-param.rrf(2); 
       rr(Nitp,3)-param.rrf(3)  ];

식 (3)의 운동 미분방정식은 LGL 콜로케이션 포인트에 배치시켜 다음 식을 만족시키도록 한다.

$[\begin{matrix} D_{11} & \dots & D_{1 N} \\ ⋮ & ⋱ & ⋮ \\ D_{N 1} & \dots & D_{N N} \end{matrix}] [\begin{matrix} R_{1}^{T} \\ ⋮ \\ R_{N}^{T} \end{matrix}] = \frac{(t_{f} - t_{0})}{2} [\begin{matrix} V_{1}^{T} \\ ⋮ \\ V_{N}^{T} \end{matrix}]$

% dynamic constraints  rr_dot=vv
F = vv;

for n=1:3 % state number
    ceq=[ceq;
         Dji*rr(:,n)-(tf-t0)/2*F(:,n)];
end

최적화 대상 변수는 다음과 같다.

$(R_{1}, R_{2}, . . ., R_{N}), (V_{1}, V_{2}, . . ., V_{N})$

pinput_0 = [rr1_0; rr2_0; rr3_0; vv1_0; vv2_0; vv3_0];

이제 매트랩의 비선형 최적화 문제 솔버인 'fmincon' 함수를 이용하여 위 문제를 풀면 된다.

% Using MATLAB nonlinear optimization solved 'fmincon' 

Aineq = []; Bineq = []; % no linear inequality constraints
Aeq = []; Beq = []; % no equality constraints

LBx=-Inf*ones(3*Nitp,1);
UBx=Inf*ones(3*Nitp,1);

LBu=-Inf*ones(3*N,1);
UBu=Inf*ones(3*N,1);

LB = [LBx; LBu];  % lower bound on the unknown variables
UB = [UBx; UBu]; % upper bound on the unknown variables

options = optimset('display','iter','diffmaxchange',1.1*1e-7,'diffminchange',1e-7,'MaxFunEvals',50000);

[presult,optfval] = ...
    fmincon(@ExLambert_L_cost,pinput_0,Aineq,Bineq,Aeq,Beq,LB,UB,@ExLambert_L_cons,options,param);

결과는 다음과 같다.

$\begin{aligned} V_{1} = {[\begin{array}{c} - 5.99248 & 1.92535 & 3.24562 \end{array}]}^{T} k m / s \\ V_{N} = {[\begin{array}{c} - 3.31249 & - 4.19662 & - 0.38531 \end{array}]}^{T} k m / s \end{aligned}$

초기속도 오차의 크기는 $0.0256 m / s$ , 최종속도 오차의 크기는 $0.0285 m / s$ 로서 해가 정확함을 알 수 있다.

아래 그림은 궤도와 위치벡터, 속도벡터, 에너지의 궤적을 그린 것이다. 에너지가 일정하게 나오므로 LPM 으로 푼 램버트 문제의 해가 안정적임을 보여준다.

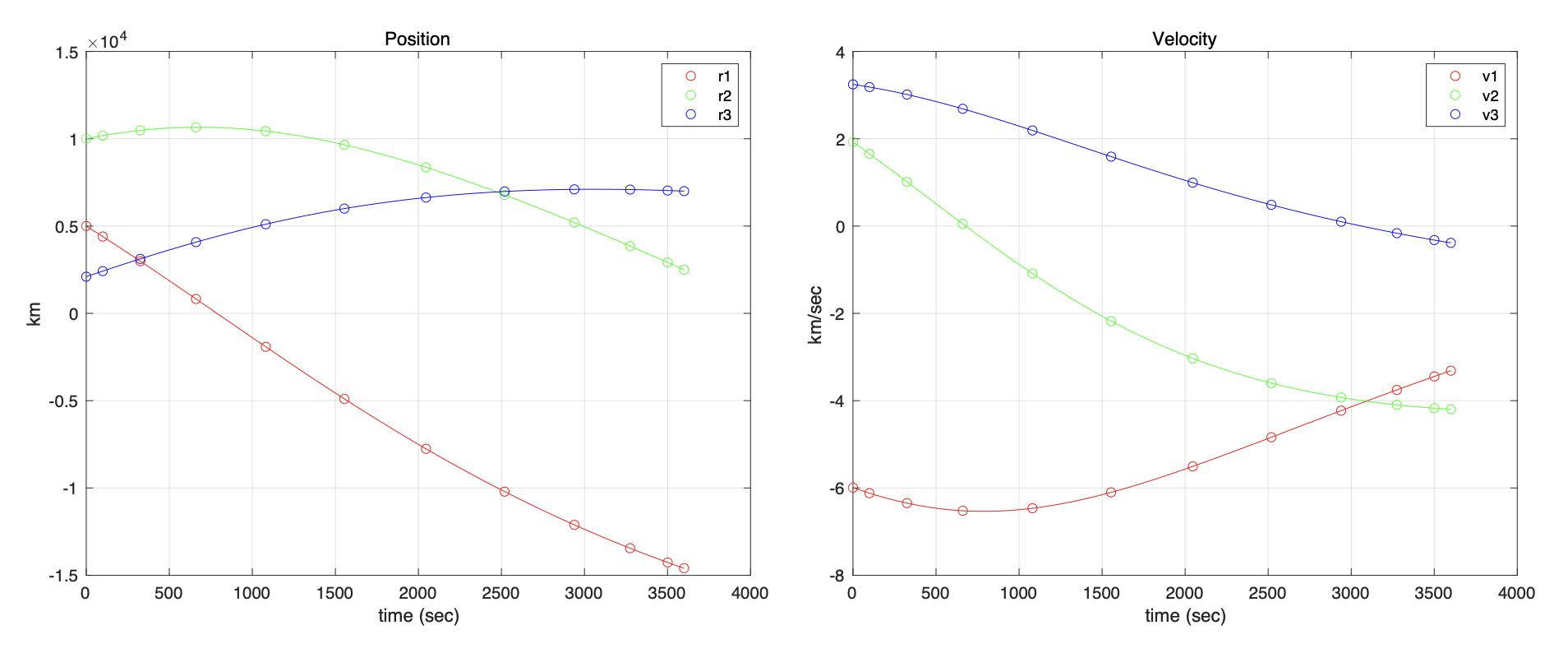
전체 매트랩 코드는 다음과 같다.

ExLambert_L_main.m

%
% Standard Lambert problem
%
% main
% using LGL pseudospectral method
% J= Lambert 
%
% Needs GaussPoints.m  LagrangePolyDerivative.m  GaussianQuadrature.m
%
% coded by st.watermelon
%

clear all; 
close all; % starting with a clean slate

% parameters
mu_orig=398600; % mu=GM
DU=6378;
TU=DU^(3/2)/sqrt(mu_orig);
DUTU=DU/TU;

mu=1;
t0=0;

% problem formulation
tf_orig=60*60;

rr0_0=[5000 10000  2100]';
rrf_0=[-14600  2500  7000]';

%----------- ref value -----------------
v0_orig = [-5.992494639666394 1.925363415280893 3.245636528490489]'; 
vf_orig = [-3.312460310936790 -4.196617307926468 -0.385287617068105]';
E_0 =(vf_orig'*vf_orig)/2-mu_orig/(sqrt(rrf_0'*rrf_0)); % specified energy
%----------- ref value -----------------

rr0=rr0_0/DU;
rrf = rrf_0/DU;
tf = tf_orig/TU;

% parameters for pseudospectral
N=12;  % number of collocation points
points=GaussPoints(N,'LGL'); % LGL collocation points (N)
col_point=points';
int_point=col_point; % interpolating points (N)
Dji=LagrangePolyDerivative(col_point,int_point); % Differentiation matrix
gweights=GaussianQuadrature(N,'LGL'); % LGL quadrature weights

% collecting parameters into param
param.Dji=Dji;
param.gweights=gweights;
param.N=N;
param.rr0=rr0;
param.rrf=rrf;
param.mu=mu;
param.t0=t0;
param.tf=tf;

% initial guesses for optimization variables (X and U)
Nitp=N;
rr1_0=zeros(Nitp,1); rr1_0(1)=rr0(1);
rr2_0=zeros(Nitp,1); rr2_0(1)=rr0(2);
rr3_0=zeros(Nitp,1); rr3_0(1)=rr0(3);

vv1_0=zeros(N,1); 
vv2_0=zeros(N,1); 
vv3_0=zeros(N,1); 

tf0=10;

% arrange initial guessed for the unknowns into a single vector
pinput_0 = [rr1_0; rr2_0; rr3_0; vv1_0; vv2_0; vv3_0];


% Using MATLAB nonlinear optimization solved 'fmincon' 

Aineq = []; Bineq = []; % no linear inequality constraints
Aeq = []; Beq = []; % no equality constraints

LBx=-Inf*ones(3*Nitp,1);
UBx=Inf*ones(3*Nitp,1);

LBu=-Inf*ones(3*N,1);
UBu=Inf*ones(3*N,1);

LB = [LBx; LBu];  % lower bound on the unknown variables
UB = [UBx; UBu]; % upper bound on the unknown variables

options = optimset('display','iter','diffmaxchange',1.1*1e-7,'diffminchange',1e-7,'MaxFunEvals',50000);

[presult,optfval] = ...
    fmincon(@ExLambert_L_cost,pinput_0,Aineq,Bineq,Aeq,Beq,LB,UB,@ExLambert_L_cons,options,param);

% results
rr1_res=presult(1:Nitp);
rr2_res=presult(Nitp+1:2*Nitp);
rr3_res=presult(2*Nitp+1:3*Nitp);

vv1_res=presult(3*Nitp+1:4*Nitp);
vv2_res=presult(4*Nitp+1:5*Nitp);
vv3_res=presult(5*Nitp+1:6*Nitp);


% Lagrange interpolating polynomials
tau=linspace(-1,1,300)';
dataset_rr1=[int_point' rr1_res];
dataset_rr2=[int_point' rr2_res];
dataset_rr3=[int_point' rr3_res];
dataset_vv1=[col_point' vv1_res]; % no u at 1 (final point)
dataset_vv2=[col_point' vv2_res]; 
dataset_vv3=[col_point' vv3_res]; 

p_rr1=LagrangePoly(dataset_rr1,tau);
p_rr2=LagrangePoly(dataset_rr2,tau);
p_rr3=LagrangePoly(dataset_rr3,tau);
p_vv1=LagrangePoly(dataset_vv1,tau);
p_vv2=LagrangePoly(dataset_vv2,tau);
p_vv3=LagrangePoly(dataset_vv3,tau);

tt=((tf-t0)*tau+(tf+t0))/2*TU; % convert to t from tau

% plotting
figure,plot(((tf-t0)*dataset_rr1(:,1)+(tf+t0))/2*TU,dataset_rr1(:,2)*DU,'ro', ...
            ((tf-t0)*dataset_rr2(:,1)+(tf+t0))/2*TU,dataset_rr2(:,2)*DU,'go', ...
            ((tf-t0)*dataset_rr3(:,1)+(tf+t0))/2*TU,dataset_rr3(:,2)*DU,'bo',...
            tt,p_rr1*DU,'r', tt,p_rr2*DU,'g', tt,p_rr3*DU,'b')
legend('r1','r2','r3')
grid

figure,plot(((tf-t0)*dataset_vv1(:,1)+(tf+t0))/2*TU,dataset_vv1(:,2)*DUTU,'ro', ...
            ((tf-t0)*dataset_vv2(:,1)+(tf+t0))/2*TU,dataset_vv2(:,2)*DUTU,'go', ...
            ((tf-t0)*dataset_vv3(:,1)+(tf+t0))/2*TU,dataset_vv3(:,2)*DUTU,'bo', ...
            tt,p_vv1*DUTU,'r',tt,p_vv2*DUTU,'g', tt,p_vv3*DUTU,'b')
legend('v1','v2','v3')
grid
        
figure, plot3(dataset_rr1(:,2)*DU,dataset_rr2(:,2)*DU,dataset_rr3(:,2)*DU,'ro',...
              p_rr1*DU,p_rr2*DU,p_rr3*DU, 'r', 0,0,0,'go', ...
              dataset_rr1(1,2)*DU,dataset_rr2(1,2)*DU,dataset_rr3(1,2)*DU,'b*');
          xlabel('x');ylabel('y');zlabel('z'); grid

          
          
Ener = ((dataset_vv1(:,2)).^2+(dataset_vv2(:,2)).^2 + ...
          (dataset_vv3(:,2)).^2).*(DUTU)^2./2 -  ...
          mu_orig./(DU.*sqrt(((dataset_rr1(1:N,2)).^2+(dataset_rr2(1:N,2)).^2 + ...
          (dataset_rr3(1:N,2)).^2)));
figure, plot(((tf-t0)*dataset_vv1(:,1)+(tf+t0))/2*TU, Ener,'bo');
          xlabel('time(sec)');ylabel('Ener'); grid
          
format long

disp('ref vs computed initial velocity......................');
VV0=[dataset_vv1(1,2) dataset_vv2(1,2) dataset_vv3(1,2)]'*DUTU;
[v0_orig VV0]
disp('ref vf vs computed vf......................');
VVf = [dataset_vv1(end,2); dataset_vv2(end,2); dataset_vv3(end,2)]*DUTU;
[vf_orig VVf]
disp('errors of initial and final velocity......................');
norm(v0_orig-VV0)
norm(vf_orig-VVf)
disp('ref Energy vs computed Energy......................');
RR0=[dataset_rr1(1,2) dataset_rr2(1,2) dataset_rr3(1,2)]*DU;
[E_0 (norm(VV0))^2/2-mu_orig/norm(RR0)]

ExLambert_L_cost.m

%
% Standard Lambert problem
%
% Cost function
%
% coded by st.watermelon
%

function rcost = ExLambert_L_cost(pinput,param)

ww=param.gweights;
N=param.N;
mu=param.mu;
t0=param.t0;
tf=param.tf;

Nitp=N;

ep=1e-10;

rr(:,1)=pinput(1:Nitp);
rr(:,2)=pinput(Nitp+1:2*Nitp);
rr(:,3)=pinput(2*Nitp+1:3*Nitp);

vv(:,1)=pinput(3*Nitp+1:4*Nitp);
vv(:,2)=pinput(4*Nitp+1:5*Nitp);
vv(:,3)=pinput(5*Nitp+1:6*Nitp);

rsum=0;
for ii=1:N
    rsum=rsum+ww(ii)/sqrt(rr(ii,1)*rr(ii,1)+ ...
         rr(ii,2)*rr(ii,2)+rr(ii,3)*rr(ii,3)+ep);
end

vsum=(ww.*vv(:,1))'*vv(:,1)+(ww.*vv(:,2))'*vv(:,2)+(ww.*vv(:,3))'*vv(:,3);
rcost = (tf-t0)/2*((0.5*vsum)+mu*rsum);

ExLambert_L_cons.m

%
% Standard Lambert problem
%
% Constraints
%
% coded by st.watermelon
%

function [cineq,ceq] = ExLambert_L_cons(pinput,param)
%
% constraints
%
N=param.N;
Dji=param.Dji;
t0=param.t0;
tf=param.tf;

Nitp=N;

rr(:,1)=pinput(1:Nitp);
rr(:,2)=pinput(Nitp+1:2*Nitp);
rr(:,3)=pinput(2*Nitp+1:3*Nitp);

vv(:,1)=pinput(3*Nitp+1:4*Nitp);
vv(:,2)=pinput(4*Nitp+1:5*Nitp);
vv(:,3)=pinput(5*Nitp+1:6*Nitp);


% inequality constraints
cineq = []; 

% dynamic constraints  rr_dot=vv
F = vv;
      
% equality constraints
ceq = [rr(1,1)-param.rr0(1); 
       rr(1,2)-param.rr0(2); 
       rr(1,3)-param.rr0(3); 
       rr(Nitp,1)-param.rrf(1); 
       rr(Nitp,2)-param.rrf(2); 
       rr(Nitp,3)-param.rrf(3)  ];
      

for n=1:3 % state number
    ceq=[ceq;
         Dji*rr(:,n)-(tf-t0)/2*F(:,n)];
end

'유도항법제어 > 최적제어' 카테고리의 다른 글

[Continuous-Time] 무한구간 (Infinite-horizon) LQR (0)	2023.12.21
[Continuous-Time] 자유최종상태 (Free-final-state) LQR (0)	2023.12.19
[PSOC-11] 가우스 유사 스펙트럴 (GPM) 기반 최적제어 (0)	2023.07.20
[PSOC-10] 라다우 유사 스펙트럴 (RPM) 기반 최적제어 (0)	2023.07.18
[PSOC-9] 로바토 유사 스펙트럴 (LPM) 기반 최적제어 (0)	2023.07.17

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

DeepCampus

[PSOC-12] 예제 : 램버트 문제 (Lambert’s problem)

'유도항법제어 > 최적제어' 카테고리의 다른 글

댓글

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역

[PSOC-12] 예제 : 램버트 문제 (Lambert’s problem)

'유도항법제어 > 최적제어' 카테고리의 다른 글

관련글

댓글

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역