다음과 같이 미지의 이산시간(discrete-time) 선형 시스템이 있다고 하자.
\[ \begin{align} & \mathbf{x}_{k+1}=A \mathbf{x}_k+B \mathbf{u}_k \tag{1} \\ \\ & \mathbf{y}_k=C \mathbf{x}_k+D \mathbf{u}_k \end{align} \]
여기서 \(\mathbf{x}_k \in \mathbb{R}^n\), \(\mathbf{u}_k \in \mathbb{R}^p\), \(\mathbf{y}_k \in \mathbb{R}^q\), \(A \in \mathbb{R}^{n \times n}\), \(B \in \mathbb{R}^{n \times p}\), \(C \in \mathbb{R}^{q \times n}\), \(D \in \mathbb{R}^{q \times p}\) 이다.
이 시스템의 마코프 파라미터 \(Y_i\) 가 주어졌을 때,
\[ Y_i= \begin{cases} D, & i=0 \\ CA^{i-1}B, & i>0 \end{cases} \tag{2} \]
시스템 (1)의 행렬 \(A, B, C, D\) 및 차수(order) \(n\) 을 추정할 수 있을까. 즉, 시스템을 식별(identification)할 수 있을까.
식별하기에 앞서서 위 시스템의 가관측성(observability) 행렬 \(\mathcal{O}_n\)와 가제어성(controllability) 행렬 \(\mathcal{R}_n\) 을 서로 곱해보자.
\[ \begin{align} \mathcal{O}_n \mathcal{R}_n &= \begin{bmatrix} C \\ CA \\ CA^2 \\ \vdots \\ CA^{n-1} \end{bmatrix} \begin{bmatrix} B & AB & A^2 B & \cdots & A^{n-1} B \end{bmatrix} \tag{3} \\ \\ &= \begin{bmatrix} CB & CAB & CA^2 B & \cdots & CA^{n-1} B \\ CAB & CA^2 B & CA^3 B & \cdots & CA^n B \\ CA^2 B & CA^3 B & CA^4 B & \cdots & CA^{n+1} B \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ CA^{n-1} B & CA^n B & CA^{n+1} B & \cdots & CA^{2n-2} B \end{bmatrix} \end{align} \]
식 (3)의 행렬은 항켈(Hankel) 행렬이 되고 각 구성 성분은 \(Y_0\) 를 제외한 마코프 파라미터인 것을 알 수 있다. 따라서 식 (3)은 다음과 같이 쓸 수 있다.
\[ \mathcal{H} = \mathcal{O}_n \mathcal{R}_n = \begin{bmatrix} Y_1 & Y_2 & \cdots & Y_n \\ Y_2 & Y_3 & \cdots & Y_{n+1} \\ \vdots & \vdots & \ddots & \vdots \\ Y_n & Y_{n+1} & \cdots & Y_{2n-1} \end{bmatrix} \tag{4} \]
Ho-Kalman 식별 알고리즘은 미지의 시스템의 마코프 파라미터 \(Y_i\) 가 주어졌을 때 시스템 행렬 \(A, B, C, D\) 및 차수 \(n\) 을 추정하는 알고리즘이다.
행렬 \(D\) 는 \(Y_0\) 와 같으므로 바로 추정이 가능하고, 행렬 \(A, B, C\) 와 차수 \(n\) 은 마코프 파라미터를 이용하여 항켈 행렬을 구성한 다음 추정한다. 다음과 같이 행이 \(r\), 열이 \(s\) 인 항켈 행렬 \(\mathcal{H}_{r,s} (0)\) 을 정의한다.
\[ \mathcal{H}_{r,s}(0) = \begin{bmatrix} Y_1 & Y_2 & \cdots & Y_s \\ Y_2 & Y_3 & \cdots & Y_{s+1} \\ \vdots & \vdots & \ddots & \vdots \\ Y_r & Y_{r+1} & \cdots & Y_{r+s-1} \end{bmatrix} \in \mathbb{R}^{qr \times ps} \tag{5} \]
식 (5)의 행렬을 \(\mathcal{H}_{r,s}(0)= \mathcal{O}_r \mathcal{R}_s\) 로 분할하면 다음과 같다.
\[ \mathcal{O}_r= \begin{bmatrix} C \\ CA \\ CA^2 \\ \vdots \\ CA^{r-1} \end{bmatrix}, \ \ \ \mathcal{R}_s= \begin{bmatrix} B & AB & A^2 B & \cdots & A^{s-1} B \end{bmatrix} \tag{6} \]
여기서 \(r\) 과 \(s\) 는 예상되는 시스템의 차수 \(n\) 보다 크게 잡아야 한다. 만약 시스템의 차수가 \(n\) 이면 마코프 파라미터를 \(r \gt n\), \(s \gt n\) 이상 쌓아도 항켈 행렬 \(\mathcal{H}_{r,s}(0)\) 의 랭크(rank)는 \(n\) 이 될 것이므로, 행렬 \(\mathcal{H}_{r,s}(0)\) 의 랭크가 더 이상 증가하지 않을 때까지 마코프 파라미터를 추가하고 시스템의 차수 \(n\) 을 다음과 같이 계산하면 된다.
\[ n=rank(\mathcal{H}_{r,s} (0)) \tag{7} \]
그러나 실제 적용에 있어서는 노이즈나 다른 영향으로 인하여 \(\mathcal{H}_{r,s}(0)\) 의 랭크가 계속 증가할 수 있다. 이럴 경우에는 다음과 같이 특이값 분해(SVD, singular value decomposition)를 이용하여 특이값이 현격하게 차이나는 지점을 시스템의 차수 \(n\) 으로 정한다.
\[ \begin{align} \mathcal{H}_{r,s} (0) &= U \Sigma V^T \approx U_n \Sigma_n V_n^T \tag{8} \\ \\ &= U_n \Sigma_n^{1/2} \Sigma_n^{1/2} V_n^T \\ \\ &= \hat{\mathcal{O}}_r \hat{\mathcal{R}}_s \end{align} \]
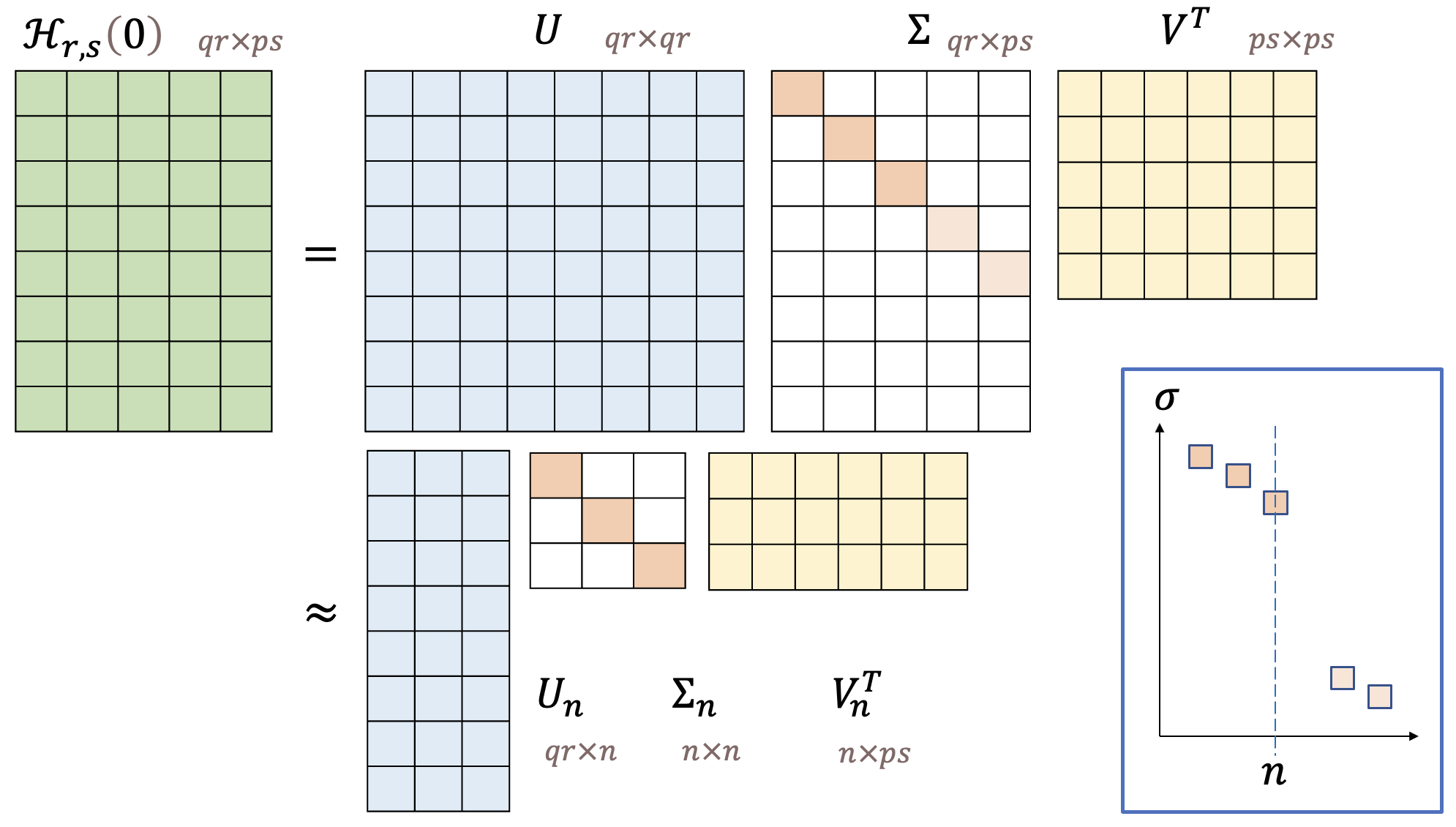
식 (6)과 (8)에 의하면 \(\hat{\mathcal{O}}_r\) 과 \(\hat{\mathcal{R}}_s\) 는 각각 다음과 같다.
\[ \begin{align} & \hat{\mathcal{O}}_r= \begin{bmatrix} C \\ CA \\ CA^2 \\ \vdots \\ CA^{r-1} \end{bmatrix} =U_n \Sigma_n^{1/2} \tag{9} \\ \\ & \hat{\mathcal{R}}_s= \begin{bmatrix} B & AB & A^2 B & \cdots & A^{s-1} B \end{bmatrix} = \Sigma_n^{1/2} V_n^T \end{align} \]
이제 행렬 \(A, B, C\) 를 추정하기 위하여 다음과 같이 항켈 행렬 \(\mathcal{H}_{r,s} (0)\) 을 한칸 이동시킨 항켈 행렬 \(\mathcal{H}_{r,s} (1)\) 을 정의한다.
\[ \begin{align} \mathcal{H}_{r,s} (1) & = \begin{bmatrix} Y_2 & Y_3 & \cdots & Y_{s+1} \\ Y_3 & Y_4 & \cdots & Y_{s+2} \\ \vdots & \vdots & \ddots & \vdots \\ Y_{r+1} & Y_{r+2} & \cdots & Y_{r+s} \end{bmatrix} \ \ \in \mathbb{R}^{qr \times ps} \tag{10} \\ \\ &= \begin{bmatrix} C \\ CA \\ CA^2 \\ \vdots \\ CA^{r-1} \end{bmatrix} A \begin{bmatrix} B & AB & A^2 B & \cdots & A^{s-1} B \end{bmatrix} \end{align} \]
식 (9)에 의하면 \(\mathcal{H}_{r,s} (1)\) 은 다음과 같이 근사화 할 수 있다.
\[ \mathcal{H}_{r,s} (1) \approx U_n \Sigma_n^{1/2} A \Sigma_n^{1/2} V_n^T \tag{11} \]
식 (11)로부터 A는 다음과 같이 계산할 수 있다.
\[ \hat{A} = \Sigma_n^{-1/2} U_n^T \mathcal{H}_{r,s} (1) V_n \Sigma_n^{-1/2} \tag{12} \]
식 (9)의 \(\hat{\mathcal{R}}_s\) 로부터 \(B\) 는 다음과 같이 계산할 수 있다.
\[ \begin{align} \hat{B} &= \begin{bmatrix}B & AB & \cdots & A^{s-1} B \end{bmatrix} \begin{bmatrix}I_p \\ 0 \\ \vdots \\ 0 \end{bmatrix} \tag{13} \\ \\ &= \Sigma_n^{1/2} V_n^T E_p \end{align} \]
식 (9)의 \(\hat{\mathcal{O}}_r\) 로부터 \(C\) 는 다음과 같이 계산할 수 있다.
\[ \begin{align} \hat{C} &= \begin{bmatrix} I_q & 0 & \cdots & 0 \end{bmatrix} \begin{bmatrix} C \\ CA \\ \vdots \\ CA^{r-1} \end{bmatrix} \tag{14} \\ \\ &= E_q U_n \Sigma_n^{1/2} \end{align} \]
Ho-Kalman 식별 알고리즘을 정리하면 다음과 같다.
1. 미지의 시스템의 임펄스 반응을 이용하여 마코프 파라미터를 구한다.
2. 마코프 파라미터로 항켈 행렬 \(\mathcal{H}_{r,s} (0)\), \(\mathcal{H}_{r,s} (1)\) 을 만든다.
3. 항켈 행렬 \(\mathcal{H}_{r,s} (0)\) 의 SVD를 계산하고 시스템 차수를 구한다.
4. 시스템 행렬 \(A, B, C, D\) 를 계산한다.
'유도항법제어 > 데이터기반제어' 카테고리의 다른 글
| OKID (Observer Kalman Filter Identification) (0) | 2023.03.25 |
|---|---|
| ERA (Eigensystem Realization Algorithm) (0) | 2023.03.25 |
| 마코프 파라미터 (Markov Parameters) (0) | 2023.03.22 |
| [DMD-3] DMDior (0) | 2022.11.08 |
| [DMD-2] DMDio (0) | 2022.10.31 |




댓글