PX4의 멀티콥터(multicopter) 비행제어기는 자세/각속도 제어기인 내부루프와 위치 제어기인 외부루프로 구성되어 있다.
위치 제어기는 내부나 외부 임무 모듈로부터 멀티콥터의 목표 궤적(desired trajectory)을 받아서 추력의 크기와 자세 명령(attitude setpoint)을 생성하고, 자세/각속도 제어기는 이를 받아서 추력과 모멘트 명령을 생성하게 된다. 최종적으로 제어력 할당 모듈을 통해서 멀티콥터의 로터 회전속도를 제어한다.
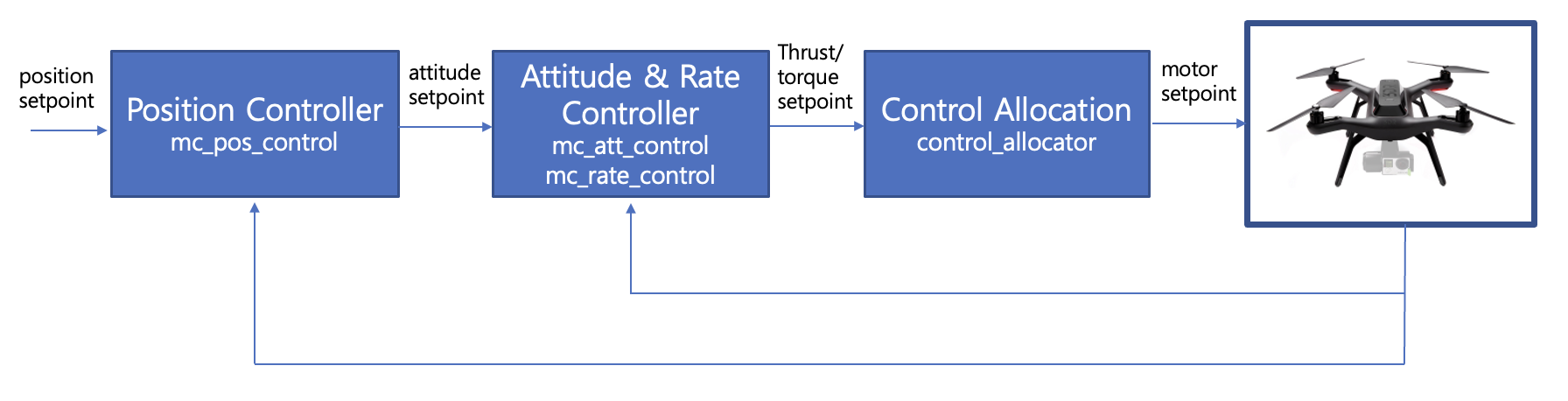
자세 제어기는 각속도 명령을 생성해 내며 각속도 제어기는 이를 받아서 추력과 모멘트 명령을 생성한다. 자세 제어기는 \(250 Hz\), 각속도 제어기는 \(1 kHz\), 위치 제어기는 \(50 Hz\) 의 빠르기로 작동한다. 따라서 내부루프는 외부루프에 비해서 충분히 빠르게 작동하기 때문에 시간분리(time-scale separation)가 가능하므로 각각 독립적으로 설계할 수 있다.
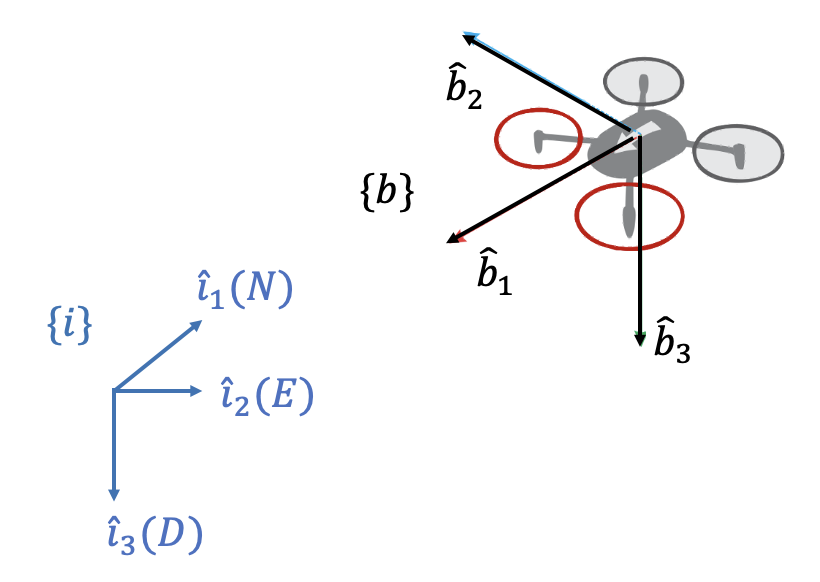
PX4에서는 전통적으로 항공분야에서 사용하는 NED(north-east-down) 좌표계를 관성 좌표계 \(\{i\}\) 로 사용한다. 동체 좌표계 \(\{b\}\)도 동체의 아래 방향, 즉 멀티콥터의 추력 방향의 반대 방향을 \(z\) 축으로 삼는다.
PX4 멀티콥터 자세 제어기는 v1.8.0 이후부터 기술보고서 'Nonlinear Quadcopter Attitude Control Technical Report, 2013' 에 기반을 두고 있다. 그 이전 버전에서는 Anton Babushkin이라는 사람의 아이디어에 기반한 알고리즘을 사용하였다. 나름 재미있는 요소가 많이 있으나 안정성(stability) 증명은 없었다. 기술 보고서에 기반한 새로운 알고리즘은 휴리스틱한 요소도 일부 들어가 있긴 하지만 기본적으로 안정성이 이론적으로 증명된 것이다.
이 보고서에서는 자세제어 알고리즘에서 가장 많이 사용되고 있는 쿼터니언(quaternion)을 이용하였다(https://pasus.tistory.com/86 ). 쿼터니언은 특이점이 없고 1개의 잉여 파라미터만 있다는 장점이 있다.
멀티콥터의 자세를 \(\mathbf{q}_b^i\) 로 표시하자. \(\mathbf{q}_b^i\) 는 관성 좌표계 \(\{i\}\) 에서 동체 좌표계 \(\{b\}\) 로의 쿼터니언이라고 한다. 자세는 칼만필터 모듈에서 추정한다. 위치 제어기에서 생성한 자세 명령을 \(\mathbf{q}_{cmd}\) 라고 하자. 자세 제어기의 목적은 \(\mathbf{q}_b^i\) 와 \(\mathbf{q}_{cmd}\) 의 차이, 즉 자세 오차를 \(0\) 으로 만들도록 멀티곱터의 각속도를 생성하는 것이다.
자세 오차를 다음과 같이 곱셈형 쿼터니언 오차 \(\mathbf{q}_e\) 로 정의한다.
\[ \mathbf{q}_{cmd}= \mathbf{q}_b^i \otimes \mathbf{q}_e \tag{1} \]
자세 오차가 \(0\) 이면 쿼터니언 오차 \(\mathbf{q}_e\) 가 \(\mathbf{q}_I\) 가 됨을 의미한다. 여기서 \(\mathbf{q}_I\) 는 회전각이 \(0\) 일 때의 쿼터니언으로서 다음과 같다.
\[ \mathbf{q}_I= \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} \tag{2} \]
따라서 제어 목적은 \(\mathbf{q}_e\) 를 \(\mathbf{q}_I\) 가 되게 하는 것이다. 이제 제어 목적을 바탕으로 다음과 같이 일반적인 리야프노프 함수 후보(Lyapunov function candidate) \(V\) 를 정의한다(https://pasus.tistory.com/220).
\[ V= (\mathbf{q}_e- \mathbf{q}_I )^T (\mathbf{q}_e- \mathbf{q}_I ) \tag{3} \]
여기서
\[ \mathbf{q}_e= \begin{bmatrix} q_{e0} \\ q_{e1} \\ q_{e2} \\ q_{e3} \end{bmatrix} = \begin{bmatrix} q_{e0} \\ \mathbf{q}_{e1:3} \end{bmatrix} \tag{4} \]
이다. 식 (3)은 다음과 같이 되어서 기술보고서에 나와 있는 리야프노프 함수 후보와 일치한다.
\[ V= \mathbf{q}_{e1:3}^T \mathbf{q}_{e1:3}+(q_{e0}-1)^2 \tag{5} \]
식 (3)의 \(V\) 를 시간 미분하면 다음과 같다.
\[ \dot{V} = 2 (\mathbf{q}_e-\mathbf{q}_I )^T \dot{\mathbf{q}}_e \tag{6} \]
식 (6)을 더 전개하기 위해서는 약간의 쿼터니언 미분과 연산에 대한 지식이 필요하다. 쿼터니언에 관한 자세한 사항은 다음 책을 참고하면 좋을 것 같다.
방향코사인행렬, 오일러각, 그리고 쿼터니언
<b>“좌표계간의 상호 변환관계를 말하다”</b> <b>“물체의 자세 변화를 수학적으로 표현하고 싶은 개발자를 위한 책”</b> 이 책은 방향코사인행렬, 오일러각, 쿼터니언과 이들의 시간 변화율에
digital.kyobobook.co.kr
먼저 식 (1)에서 \(\mathbf{q}_{cmd}\) 은 상수(constant)라고 가정한다. 이 가정은 외부루프에 비해서 내부루프가 상당히 빠르게 작동하므로 유효한 가정이다. 식 (1)을 미분하면 다음과 같다.
\[ 0= \dot{\mathbf{q}}_b^i \otimes \mathbf{q}_e+ \mathbf{q}_b^i \otimes \dot{\mathbf{q}}_e \tag{7} \]
위 식에 의하면 \(\dot{\mathbf{q}}_e\) 는 다음과 같다.
\[ \begin{align} \dot{\mathbf{q}}_e &= -\left( \mathbf{q}_b^i \right)^{-1} \otimes \dot{\mathbf{q}}_b^i \otimes \mathbf{q}_e \tag{8} \\ \\ &= - \frac{1}{2} \left( \mathbf{q}_b^i \right)^{-1} \otimes \mathbf{q}_b^i \otimes \bar{\omega}_{ib}^b \otimes \mathbf{q}_e \\ \\ &= -\frac{1}{2} \bar{\omega}_{ib}^b \otimes \mathbf{q}_e \end{align} \]
여기서
\[ \bar{\omega}_{ib}^b= \begin{bmatrix} 0 \\ \omega_{ib}^b \end{bmatrix} \tag{9} \]
이고, 다음과 같은 쿼터니언의 미분을 이용하였다.
\[ \dot{\mathbf{q}}_b^i= \frac{1}{2} \mathbf{q}_b^i \otimes \bar{\omega}_{ib}^b \tag{10} \]
\( \omega_{ib}^b\) 는 좌표계 \(\{i\}\) 를 기준으로한 좌표계 \(\{b\}\) 의 각속도 벡터를 나타내는 \( ^i \vec{\omega} ^b\) 를 좌표계 \(\{b\}\) 로 표현한 것이다(https://pasus.tistory.com/120 ). 쿼터니언 곱 관계식을 이용하면 식 (8)은 다음과 같이 쓸 수 있다.
\[ \begin{align} \dot{\mathbf{q}}_e &= -\frac{1}{2} [\bar{\omega}_{ib}^b ] \mathbf{q}_e \tag{11} \\ \\ &=- \frac{1}{2} \begin{bmatrix} 0 & -\left( \omega_{ib}^b \right)^T \\ \omega_{ib}^b & [\omega_{ib}^b \times] \end{bmatrix} \begin{bmatrix} q_{e0} \\ \mathbf{q}_{e1:3} \end{bmatrix} \\ \\ &=- \frac{1}{2} \begin{bmatrix} -\mathbf{q}_{e1:3}^T \omega_{ib}^b \\ q_{e0} \omega_{ib}^b+ [\omega_{ib}^b \times] \mathbf{q}_{e1:3} \end{bmatrix} \end{align} \]
여기서 각속도 벡터 \(\omega_{ib}^b= \begin{bmatrix} \omega_1 & \omega_2 & \omega_3 \end{bmatrix}^T\) 의 빗대칭(skew-symmetric) 행렬은 다음과 같다.
\[ [\omega_{ib}^b \times]= \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} \tag{12} \]
식 (11)을 (6)에 대입하면 \(\dot{V}\) 은 다음과 같이 된다.
\[ \begin{align} \dot{V} &= - \begin{bmatrix} (q_{e0}-1) & \mathbf{q}_{e1:3}^T \end{bmatrix} \begin{bmatrix} -\mathbf{q}_{e1:3}^T \omega_{ib}^b \\ q_{e0} \omega_{ib}^b+ [\omega_{ib}^b \times] \mathbf{q}_{e1:3} \end{bmatrix} \tag{13} \\ \\ &=(q_{e0}-1) \mathbf{q}_{e1:3}^T \omega_{ib}^b-q_{e0} \mathbf{q}_{e1:3}^T \omega_{ib}^b- \mathbf{q}_{e1:3}^T [\omega_{ib}^b \times] \mathbf{q}_{e1:3} \\ \\ &= - \mathbf{q}_{e1:3}^T \omega_{ib}^b \end{align} \]
따라서 \(\dot{V} \lt 0\) 가 되기 위해서는
\[ \omega_{ib}^b=k_{cmd} \mathbf{q}_{e1:3} \tag{14} \]
이면 된다. 여기서 \(k_{cmd} \gt 0\) 은 임의의 상수로서 설계변수다.
식 (14)에 의하면 멀티콥터의 자세 \(\mathbf{q}_b^i\) 가 명령값 \(\mathbf{q}_{cmd}\) 가 되기 위해서는 각속도 벡터가 \(\omega_{ib}^b=k_{cmd} \mathbf{q}_{e1:3}\) 이어야 한다. 따라서 식 (14)를 각속도 명령이라고 하는데, 이 명령을 멀티콥터의 실제 각속도가 따라가게 하는 각속도 제어가 필요하다.
식 (14)와 같은 각속도 명령은 생각과는 달리 좋은 결과를 보여주지는 못하는 데, 그 이유는 쿼터니언의 대척점 모호성(antipodal ambiguity)과 멀티콥터의 요(yaw)운동이 피치(pitch)와 롤(roll) 운동보다 훨씬 느리다는 점을 고려하지 않았기 때문이다.
'유도항법제어 > 비행제어' 카테고리의 다른 글
| [PX4] 멀티콥터 자세제어 알고리즘 - 3 (0) | 2023.02.24 |
|---|---|
| [PX4] 멀티콥터 자세제어 알고리즘 - 2 (0) | 2023.02.23 |
| [DI-2] 내부 동역학 (Internal Dynamics) (0) | 2023.01.20 |
| [DI-1] 동적 역변환 (Dynamic Inversion) (0) | 2023.01.04 |
| 비선형 시스템과 매니폴드 (Manifold) (0) | 2023.01.01 |




댓글