최적제어(optimal control)문제는 여러 가지 물리적인 제약조건을 만족하면서 어떤 성능지표(performance index) 또는 목적함수(objective function)를 최적화하도록 동적 시스템(dynamic system)의 제어변수(control variable)을 결정하는 문제이다.
제약조건(constraints)은 동적 시스템의 동역학과 함께 시스템 제어변수 및 상태변수의 경로 제약조건(path constraints), 상태변수의 초기값(initial value) 및 최종값(final value)에 관한 제약조건(constraint on the initial and final states)을 모두 포함한다. 목적함수는 설계자가 의도한대로 시스템을 움직이면서 의도한 성능을 발휘할 수 있도록, 상태변수와 제어변수에 관한 비용함수(cost function)로 주어지는 것이 일반적이다. 비용함수를 최소화하는 것이 목적함수를 최적화하는 것이다. 최적제어 문제를 수학식으로 표현하면 다음과 같다. 우선 시스템의 동역학은 다음과 같이 미분방정식으로 표현된다.
\[ \dot{\mathbf{x}}(t)= \mathbf{f}(\mathbf{x}(t), \mathbf{u}(t), t) \tag{1} \]
여기서 \(\mathbf{x}(t) \in \mathbb{R}^n\) 는 상태변수 벡터, \(\mathbf{u}(t) \in \mathbb{R}^p\) 는 제어변수 벡터이고 \(t\) 는 연속시간(continuous-time)을 의미한다. 제어변수가 최소화해야 할 목적함수는 다음과 같이 주어진다.
\[ J= \phi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) + \int_{t_0}^{t_f} g(\mathbf{x}(t), \mathbf{u}(t), t) \ dt \tag{2} \]
여기서 \(t_0\) 는 초기시간(initial time), \(t_f\) 는 최종시간(final time)이며, \(g(\mathbf{x}(t), \mathbf{u}(t), t)\) 는 운행비용(running cost), \(\phi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f )\) 는 초기시간과 최종시간에서의 비용이다. 목적함수는 제어 설계자가 의도한 대로 시스템이 반응하도록 정해진다. 초기 및 최종 상태변수 제약조건은 상태변수의 초기값과 최종값의 함수로서 다음과 같이 부등식으로 주어진다.
\[ \psi_{min} \le \psi (\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) \le \psi_{max} \tag{3} \]
여기서 \(\psi \in \mathbb{R}^m\) 로서 구성 성분이 \(m\) 개인 벡터이며 부등식은 벡터를 구성하는 각 성분의 부등식으로 해석한다. 경로 제약조건(path constraint)은 상태변수와 제어변수의 함수로서 시스템의 경로에 가해지는 제약조건을 다음과 같이 부등식으로 나타낸다.
\[ \mathbf{c}_{min} \le \mathbf{c}( \mathbf{x}(t), \mathbf{u}(t), t) \le \mathbf{c}_{max} \tag{4} \]
최적제어 문제는 동역학, 상태변수 제약조건, 경로 제약조건을 만족하면서 목적함수를 최소화시키는 제어변수 \(\mathbf{u}(t), \ t \in [t_0, t_f]\) 를 구하는 것이다.
일반 최적제어 문제는 해석적으로 접근하기가 곤란하므로, 문제를 조금 단순화시켜 보도록 한다. 일반 최적제어 문제에서 경로 제약조건을 없애고, 초기상태 및 최종 상태변수 제약조건을 등식 방정식으로 바꾼다. 그러면 최적제어 문제는 다음과 같이 단순화된다. 물론 단순화됐다고 해서 문제를 해석적으로 쉽게 풀 수 있다는 것은 아니다.
\[ \begin{align} & \min J = \phi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) + \int_{t_0}^{t_f} g(\mathbf{x}(t), \mathbf{u}(t), t) \ dt \tag{5} \\ \\ & \mbox{subject to: } \ \dot{\mathbf{x}}(t)= \mathbf{f}(\mathbf{x}(t), \mathbf{u}(t), t) \\ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \psi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) = 0 \end{align} \]
식 (5)에 상태변수의 초기값과 최종값에 대한 함수가 \(\phi\) 와 \(\psi \) 등 두 개가 있는데, \(\phi\) 는 스칼라 함수로서 목적함수의 일부이므로 그 값을 작게 만드는 게 목적이 되는 것이고,\(\psi\) 는 벡터함수로서 제약조건이므로 반드시 \(0\) 으로 만들어야 한다는 점에서 차이가 있다.
최적제어 문제를 풀기 위하여 라그랑지 곱수(Lagrange multiplier)를 도입하여 동역학식과 제약조건을 목적함수에 포함시킨다. 라그랑지 곱수 \(\lambda (t) \in \mathbb{R}^n\) 는 동역학 식에, \(\nu \in \mathbb{R}^m\) 는 제약조건에 연결시키면, 목적함수를 다음과 같이 비제약(unconstrained) 목적함수로 바꿀 수 있다.
\[ \begin{align} \tilde{J} &= \phi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) + \nu^T \psi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) \tag{6} \\ \\ & \ \ + \int_{t_0}^{t_f} \left[ g(\mathbf{x}(t), \mathbf{u}(t), t) +\lambda^T (t)\{ \mathbf{f}( \mathbf{x}(t), \mathbf{u}(t), t)- \dot{\mathbf{x}} \} \right] \ dt \end{align} \]
해밀토니안(Hamiltonian) 함수를 다음과 같이 정의하면,
\[ H(\mathbf{x}, \mathbf{u}, \lambda, t)= g(\mathbf{x}, \mathbf{u}, t) + \lambda^T \mathbf{f}( \mathbf{x}, \mathbf{u}, t) \tag{7} \]
목적함수 \(\tilde{J}\) 는 다음과 같이 된다.
\[ \begin{align} \tilde{J} &= \phi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) + \nu^T \psi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) \tag{8} \\ \\ & \ \ + \int_{t_0}^{t_f} \left[ H( \mathbf{x}, \mathbf{u}, \lambda, t) -\lambda^T \dot{\mathbf{x}} \right] \ dt \end{align} \]
먼저, 비제약 목적함수 \(\tilde{J}\) 를 구성하는 모든 변수 \(\mathbf{x}, \mathbf{u}, \lambda, \nu, \dot{\mathbf{x}}, t\) 의 증분(increment)에 따른 목적함수의 일차(first-order) 증분 \(d\tilde{J}\) 를 구해보도록 한다.
\[ \begin{align} d\tilde{J} &= \left( \frac{\partial \phi }{ \partial \mathbf{x}} + \left( \frac{\partial \psi }{ \partial \mathbf{x}} \right) ^T \nu \right) _{t_0}^T d \mathbf{x}(t_0 )+ \left( \frac{\partial \phi }{ \partial t} + \left( \frac{\partial \psi }{ \partial t} \right) ^T \nu \right) _{t_0}^T d t_0 \tag{9} \\ \\ & \ \ \ + \left( \frac{\partial \phi }{ \partial \mathbf{x}} + \left( \frac{\partial \psi }{ \partial \mathbf{x}} \right) ^T \nu \right) _{t_f}^T d \mathbf{x}(t_f )+ \left( \frac{\partial \phi }{ \partial t} + \left( \frac{\partial \psi }{ \partial t} \right) ^T \nu \right) _{t_f}^T d t_f \\ \\ & \ \ \ + \psi^T d \nu +(H- \lambda^T \dot{\mathbf{x}} )_{t_f } dt_f-(H-\lambda ^T \dot{\mathbf{x}})_{t_0 } dt_0 \\ \\ & \ \ \ + \int_{t_0}^{t_f} \left[ \left( \frac{\partial H}{\partial \mathbf{x}} \right)^T \delta \mathbf{x} +\left( \frac{\partial H}{\partial \mathbf{u}} \right)^T \delta \mathbf{u} - \lambda^T \delta \dot{\mathbf{x}}+\left( \frac{\partial H}{\partial \lambda}-\dot{\mathbf{x}} \right)^T \delta \lambda \right] \ dt \end{align} \]
위 식에서 \(\delta \dot{\mathbf{x}}\) 을 부분적분법을 이용하여 다음과 같이 바꾼다.
\[ \begin{align} -\int_{t_0}^{t_f} \lambda^T \delta \dot{\mathbf{x}} \ dt &= - \lambda^T (t_f ) \delta \mathbf{x}(t_f ) + \lambda^T (t_0 ) \delta \mathbf{x}(t_0 ) \tag{10} \\ \\ & \ \ \ \ \ +\int_{t_0}^{t_f} \dot{\lambda}^T \delta \mathbf{x} \ dt \end{align} \]
여기서 변분(variation) \(\delta \mathbf{x}(t_f )\) 와 미분(differential) \(d \mathbf{x}(t_f )\), 그리고 \(\delta \mathbf{x}(t_0 )\) 와 \(d\mathbf{x}(t_0 )\) 는 서로 다르며 다음과 같은 관계식을 갖는다는 점에 주의해야 한다.
\[ \begin{align} & d \mathbf{x}(t_0 ) = \delta \mathbf{x}(t_0 )+ \dot{\mathbf{x}}(t_0 )dt_0 \tag{11} \\ \\ & d \mathbf{x}(t_f ) = \delta \mathbf{x}(t_f )+ \dot{\mathbf{x}}(t_f )dt_f \end{align} \]
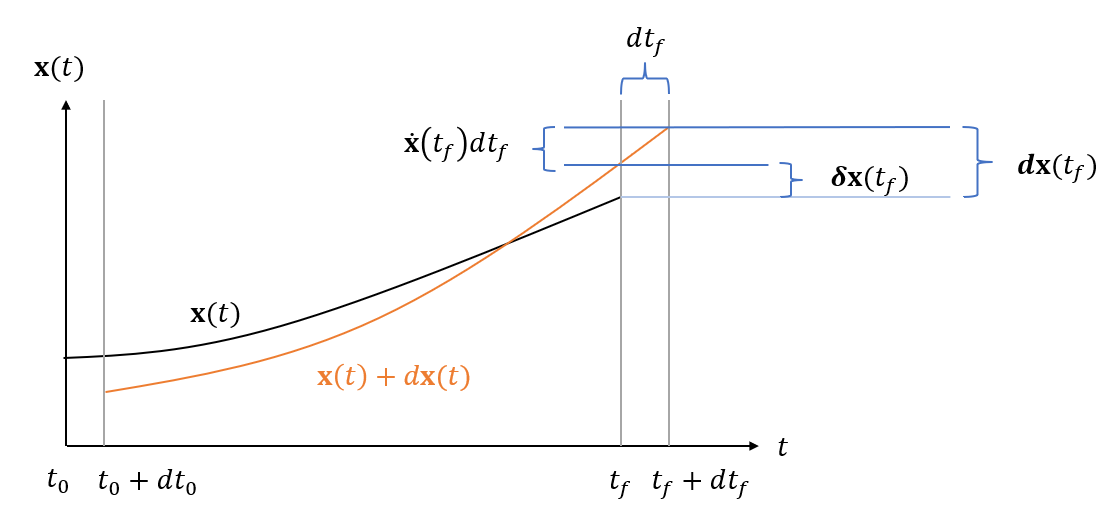
식 (10)을 (9)에 대입하면 다음과 같다.
\[ \begin{align} d\tilde{J} &= \left( \frac{\partial \phi }{ \partial \mathbf{x}} + \left( \frac{\partial \psi }{ \partial \mathbf{x}} \right) ^T \nu +\lambda \right) _{t_0}^T d \mathbf{x}(t_0 ) + \left( \frac{\partial \phi }{ \partial t} + \left( \frac{\partial \psi }{ \partial t} \right) ^T \nu - \lambda^T \dot{\mathbf{x}} \right) _{t_0}^T d t_0 \tag{12} \\ \\ & \ \ \ + \left( \frac{\partial \phi }{ \partial \mathbf{x}} + \left( \frac{\partial \psi }{ \partial \mathbf{x}} \right) ^T \nu -\lambda \right) _{t_f}^T d \mathbf{x}(t_f )+ \left( \frac{\partial \phi }{ \partial t} + \left( \frac{\partial \psi }{ \partial t} \right) ^T \nu + \lambda^T \dot{\mathbf{x}} \right) _{t_f}^T d t_f \\ \\ & \ \ \ + \psi^T d \nu +(H-\lambda ^T \dot{\mathbf{x}} )_{t_f} dt_f -(H-\lambda^T \dot{\mathbf{x}} )_{t_0} dt_0 \\ \\ & \ \ \ + \int_{t_0}^{t_f} \left[ \left( \frac{\partial H}{\partial \mathbf{x}} +\dot{\lambda} \right)^T \delta \mathbf{x} +\left( \frac{\partial H}{\partial \mathbf{u}} \right)^T \delta \mathbf{u} +\left( \frac{\partial H}{\partial \lambda}-\dot{\mathbf{x}} \right)^T \delta \lambda \right] \ dt \end{align} \]
정리하면 위 식은 다음과 같이 된다.
\[ \begin{align} d\tilde{J} &= \left( \frac{\partial \phi }{ \partial \mathbf{x}} + \left( \frac{\partial \psi }{ \partial \mathbf{x}} \right) ^T \nu +\lambda \right) _{t_0}^T d \mathbf{x}(t_0 ) + \left( \frac{\partial \phi }{ \partial t} + \left( \frac{\partial \psi }{ \partial t} \right) ^T \nu -H \right) _{t_0}^T d t_0 \tag{13} \\ \\ & \ \ \ + \left( \frac{\partial \phi }{ \partial \mathbf{x}} + \left( \frac{\partial \psi }{ \partial \mathbf{x}} \right) ^T \nu -\lambda \right) _{t_f}^T d \mathbf{x}(t_f )+ \left( \frac{\partial \phi }{ \partial t} + \left( \frac{\partial \psi }{ \partial t} \right) ^T \nu +H \right) _{t_f}^T d t_f \\ \\ & \ \ \ + \psi^T d \nu \\ \\ & \ \ \ + \int_{t_0}^{t_f} \left[ \left( \frac{\partial H}{\partial \mathbf{x}} +\dot{\lambda} \right)^T \delta \mathbf{x} +\left( \frac{\partial H}{\partial \mathbf{u}} \right)^T \delta \mathbf{u} +\left( \frac{\partial H}{\partial \lambda}-\dot{\mathbf{x}} \right)^T \delta \lambda \right] \ dt \end{align} \]
라그랑지(Lagrange) 이론에 의하면 비제약 목적함수 \(\tilde{J}\) 가 최소일 때, 본래 목적함수 \(J\) 가 최소가 된다. 따라서 본래 목적함수 \(J\) 가 최소가 되기 위한 필요조건은 \(d\tilde{j}=0\) 이므로, 위 식에서 각 변수 증분의 계수를 \(0\) 으로 놓으면 최적제어의 필요조건(necessary condition)을 얻을 수 있다. 위 식의 적분항에서 최적 조건을 구하면,
\[ \begin{align} \dot{\mathbf{x}} &= \frac{\partial H}{\partial \lambda} = \mathbf{f}(\mathbf{x}, \mathbf{u}, t) \tag{14} \\ \\ -\dot{\lambda} &= \frac{\partial H}{\partial \mathbf{x}} = \left( \frac{\partial \mathbf{f}}{\partial \mathbf{x}} \right) ^T \lambda + \frac{\partial g}{\partial \mathbf{x}} \tag{15} \\ \\ 0 &= \frac{\partial H}{\partial \mathbf{u}} = \left( \frac{\partial \mathbf{f}}{\partial \mathbf{u}} \right) ^T \lambda + \frac{\partial g}{\partial \mathbf{u}} \tag{16} \end{align} \]
이 된다. 식(14)는 시스템의 동역학인 상태변수 미분방정식이고, 식(15)는 라그랑지 곱수의 미분방정식으로서 코스테이트(costate) 방정식이라고 한다. 식(16)은 정정조건(stationary condition)이라고 한다. 이 식으로부터 최적 제어변수를 계산할 수 있다.
초기 및 최종 상태변수 제약조건은 식 (13)의 다섯 번째 항으로부터 구할 수 있다.
\[ \psi(\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f )=0 \tag{17} \]
초기시간과 최종시간에서 경계조건(boundary condition)은 식 (13)의 첫 번째에서 네 번째 항까지로 부터 구할 수 있다.
\[ \begin{align} & \left( \frac{\partial \phi }{ \partial \mathbf{x}} + \left( \frac{\partial \psi }{ \partial \mathbf{x}} \right) ^T \nu +\lambda \right) _{t_0}^T d \mathbf{x}(t_0 ) + \left( \frac{\partial \phi }{ \partial t} + \left( \frac{\partial \psi }{ \partial t} \right) ^T \nu -H \right) _{t_0}^T d t_0 = 0 \tag{18} \\ \\ & \left( \frac{\partial \phi }{ \partial \mathbf{x}} + \left( \frac{\partial \psi }{ \partial \mathbf{x}} \right) ^T \nu -\lambda \right) _{t_f}^T d \mathbf{x}(t_f )+ \left( \frac{\partial \phi }{ \partial t} + \left( \frac{\partial \psi }{ \partial t} \right) ^T \nu +H \right) _{t_f}^T d t_f =0 \tag{19} \end{align} \]
경계조건은 초기시간과 최종시간이 설정된(fixed) 값으로 주어지는지 아닌지, 그리고 초기 및 최종 상태변수가 설정된 값으로 주어지는지 아닌지에 따라 다양하게 적용할 수 있다. 만약 최종시간이 미리 설정된 값으로 주어진다면 위 식에서 \(dt_f=0\) 이 된다. 만약 상태변수의 최종값이 설정된 값이 아니고 계산해야 되는 값(free state)이라면 \(d \mathbf{x}(t_f )\ne 0\) 으로 놓는다.
해밀토니안(Hamiltonian)의 미분은 다음과 같이 된다.
\[ \frac{dH(\mathbf{x}, \mathbf{u}, \lambda ,t)}{dt} = \frac{\partial H}{\partial t}+ \left( \frac{\partial H}{\partial \mathbf{x}} \right)^T \dot{\mathbf{x}}+ \left( \frac{\partial H}{\partial \mathbf{u}} \right)^T \dot{\mathbf{u}}+\left( \frac{\partial H}{\partial \lambda} \right)^T \dot{\lambda} \tag{20} \]
식 (14), (15), (16)에 의하면 위 식은
\[ \begin{align} \frac{dH(\mathbf{x}, \mathbf{u}, \lambda ,t)}{dt} &= \frac{\partial H}{\partial t}+ \left( \frac{\partial H}{\partial \mathbf{x}} \right)^T \mathbf{f}+ \mathbf{f}^T \dot{\lambda} \tag{21} \\ \\ &= \frac{\partial H}{\partial t}+ \left( \frac{\partial H}{\partial \mathbf{x}} +\dot{\lambda} \right)^T \mathbf{f} \\ \\ &=\frac{\partial H}{\partial t} \end{align} \]
이 된다. 만약 식 (5)에서 \(\mathbf{f}\) 와 \(g\) 가 명시적으로 시간의 함수가 아니라면, 즉
\[ \begin{align} & \mathbf{f}(\mathbf{x}, \mathbf{u},t) = \mathbf{f}(\mathbf{x}, \mathbf{u}) \\ \\ & g(\mathbf{x}, \mathbf{u},t)=g(\mathbf{x}, \mathbf{u}) \end{align} \]
이라면 해밀토니안도 명시적으로 시간의 함수가 아니므로 식 (20)은 다음과 같이 된다.
\[ \frac{dH}{dt} = \frac{\partial H}{\partial t} = 0 \tag{22} \]
따라서 해밀토니안을 최적 궤적 \( ( \mathbf{x}^* (t), \mathbf{u}^* (t))\) 상에서 계산하면 상수(constant)가 됨을 알 수 있다.
지금까지 목적함수가 최소가 되기 위한 필요조건을 구했는데, 목적함수가 최소가 되기 위해서는 목적함수의 이차(second-order) 증분이 \(0\) 보다 커야 한다는, 즉, \(d^2 J \gt 0\) 이라는 충분조건(sufficient condition)이 더 필요하다. 이차 증분을 계산하는 과정이 좀 복잡한데, 결론적으로 충분조건은 다음과 같이 해밀토니안의 헤시안(Hessian)이 정정행렬(positive definite matrix)이 되어야 한다는 것으로 귀결된다. 즉,
\[ \frac{\partial }{\partial \mathbf{u}} \left( \frac{\partial H}{\partial \mathbf{u}} \right) \gt 0 \tag{23} \]
이다. 만약 제어변수가 어떤 허용된 제어변수 집합에 속해있다는 제약조건이 있다면, 즉 \(\mathbf{u} \in \mathcal{U}\) 라면, 최적 제어변수를 정정조건 \(\partial H/\partial \mathbf{u}=0\) 으로 구할 수가 없다. 폰트리아진(Pontryagin)은 이런 경우에 정정조건만 아래와 같이 보다 일반적인 조건으로 바꾸면 된다는 것을 증명하였다.
\[ \mathbf{u}^* (t)=\arg \min_{\mathbf{u} \in \mathcal{U}} H(\mathbf{x}^* (t), \mathbf{u}, \lambda^* (t), t) \tag{24} \]
여기서 위첨자 \(^*\) 는 최적값을 의미하고 \(\mathcal{U}\) 는 허용된 제어변수의 집합이다. 위 식을 폰트리아진의 최소원리(Pontryagin's minimum principle)라고 한다.
폰트리아진의 최소원리에 의하면, 최적 제어변수는 상태변수와 코스테이트의 최적값에 대해서 해밀토니안을 최소화시키는 제어변수 집합중의 한 원소가 된다. 폰트리아진의 최소원리는 다음과 같이 표현할 수도 있다.
\[ H(\mathbf{x}^*, \mathbf{u}^*, \lambda^*, t) \le H(\mathbf{x}^*, \mathbf{u}, \lambda^*, t) , \ \ \ \mathbf{u}\in \mathcal{U} \tag{25} \]
여기서 위 식은 \( H(\mathbf{x}^*, \mathbf{u}^*, \lambda^*, t) \le H(\mathbf{x}, \mathbf{u}, \lambda, t) \) 를 의미하는 것이 아니라는 점에 주의해야 한다. 폰트리아진의 최소원리는 정정조건(stationary condition) 보다 더 일반적인 조건이기 때문에 제어변수에 제약이 없는 경우에도 물론 적용할 수 있다. 허용된 제어변수의 집합을 무한대로 확장시키면 되기 때문이다. 또한 폰트리아진의 최소원리는 해밀토니안을 최소값으로 만드는 제어변수를 구하는 것이기 때문에, 해밀토니안의 헤시안(Hessian)이 정정행렬(positive-definite matrix)이 되어야 한다는 충분조건도 포함하고 있다.
일반적으로 간단한 문제의 경우에도 최적제어 해는 계산하기가 매우 어려우며 오픈-루프 제어(open-loop control) 형태로 산출된다.
'유도항법제어 > 최적제어' 카테고리의 다른 글
| [Continuous-Time] 최종상태제약 (Final-state-constrained) LQR (0) | 2023.04.08 |
|---|---|
| [Continuous-Time] 최적제어 예제 (0) | 2022.12.14 |
| [MPC] MPC를 위한 두가지 QP 모델 - 2 (0) | 2022.12.03 |
| [MPC] MPC를 위한 두가지 QP 모델 - 1 (0) | 2022.11.30 |
| [MPC] 모델예측제어 개요 (0) | 2022.11.28 |




댓글