동차 좌표(Homogeneous Coordinates)는 컴퓨터 비전과 그래픽스에서 3차원 공간의 점을 2차원 이미지로 투영하거나 다양한 기하학적 변환을 수행할 때 활용되는 수학적 표현 방식으로, 일반적으로 \(N\)차원의 점을 \(N+1\) 차원의 좌표로 확장하여 나타낸다.
예를 들어, 2차원 좌표 \((x, y)\)는 동차 좌표계에서 추가 차원을 도입하여 \(\begin{bmatrix} x & y & 1 \end{bmatrix}^T \)로 표현한다. 또한 3차원 좌표 \((x, y, z)\)는 동차 좌표계에서 \(\begin{bmatrix} x & y & z & 1 \end{bmatrix}^T \)로 표현한다.
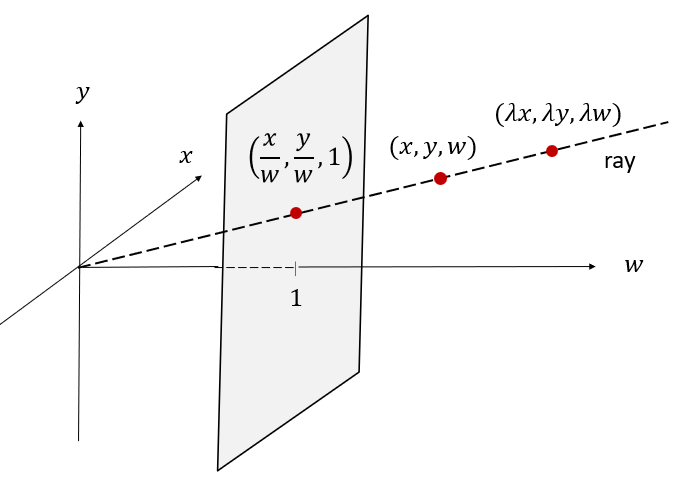
동차 좌표 \(\begin{bmatrix} x & y & w \end{bmatrix}^T \)를 원래의 2차원 좌표로 환원하려면, 마지막 성분 \(w \)로 앞의 성분들을 나누어 \((x/w, y/w)\)로 계산한다. 마찬가지로 동차 좌표 \(\begin{bmatrix} x & y & z & w \end{bmatrix}^T \)를 다시 원래의 3차원 좌표로 바꾸면 \((x/w, y/w, z/w)\)이다.
동차 좌표에서는 \(0\)이 아닌 임의의 상수 \(\lambda\)를 곱해도 동일한 점을 표현한다. 즉, \(\begin{bmatrix} x & y & w \end{bmatrix}^T \)와 \(\begin{bmatrix} \lambda x & \lambda y & \lambda w \end{bmatrix}^T \)는 동일한 점을 나타내는데 이는 두 좌표가 원점을 지나는 동일한 Ray 상에 존재하기 때문이다.
동차 좌표계를 사용하는 이유는 비선형적인 원근 투영(perspective projection) 과정을 선형 행렬 연산으로 다룰 수 있게 해주기 때문이다. 예를 들어 3차원 점 \((x, y, z)\)를 이미지 평면에 투영하려면 깊이 값 \(z\)로 나누는 연산이 필요하다 \( \left( f x/z, f y/z \right) \). 나눗셈은 비선형 연산이므로 선형 행렬식으로 표현할 수 없다. 하지만 동차 좌표를 사용하면, 다음과 같은 형태의 선형 방정식으로 표현할 수 있다.
\[ \begin{bmatrix} fx \\ fy \\ z \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \]
동차 좌표계는 직교 좌표계에서 별도로 다뤄야 하는 평행이동(translation)과 회전(rotation)을 하나의 \(3 \times 3\) 또는 \(4 \times 4\) 행렬 곱셈으로 통합하여 표현할 수 있게 한다.
예를 들어 평행이동은 벡터의 덧셈으로 \( \mathbf{x}'= \mathbf{x}+\mathbf{t}\) 로 표현하고 회전은 DCM을 이용한 곱셈 \(\mathbf{x}'=C \mathbf{x}\) 로 표현되어 두 연산의 형식이 다르다. 하지만 동차 좌표로 확장하면 이들 변환을 다음과 같이 동일한 행렬 곱셈 형태로 표현할 수 있다.
\[ \begin{bmatrix} \mathbf{x}' \\ 1 \end{bmatrix} = \begin{bmatrix} I & \mathbf{t} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ 1 \end{bmatrix}, \quad \begin{bmatrix} \mathbf{x}' \\ 1 \end{bmatrix} = \begin{bmatrix} C & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ 1 \end{bmatrix} \]
평행이동과 회전의 조합도 동차 좌표계에서 단일 행렬 연산으로 통합적으로 표현될 수 있다.
\[ \begin{bmatrix} \mathbf{x}' \\ 1 \end{bmatrix} = \begin{bmatrix} C & \mathbf{t} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ 1 \end{bmatrix} \]
또한 직교 좌표계에서는 무한대에 있는 점을 숫자로 표현할 수 없지만, 동차 좌표계에서는 마지막 성분을 \(0\)으로 두어 무한대 점을 표현할 수 있다. 이는 평행한 선들이 만나는 소실점(Vanishing Point)을 수학적으로 계산하고 표현하는 데 중요하다.
'유도항법제어 > 유도항법' 카테고리의 다른 글
| 두빈스 경로 (Dubins Path) - 2 (0) | 2024.05.25 |
|---|---|
| 두빈스 경로 (Dubins Path) - 1 (0) | 2024.05.25 |
| 화성 착륙 과정과 진입 운동방정식 (0) | 2024.04.28 |
| [INS] 관성항법시스템 오차 방정식 (INS Error Equations) (0) | 2024.03.15 |
| [INS] 관성항법 방정식 (Kinematics of Inertial Navigation) (0) | 2024.03.03 |




댓글