J2 섭동에 의한 궤도요소의 시간 변화율 - 1

J2 섭동에 의한 궤도요소(orbital elements)의 시간 변화율은 라그랑지 행성 방정식(Lagrange planetary equation)이나 가우스 행성 방정식(Gauss planetary equation)을 이용하여 계산할 수 있다. 여기서는 가우스 행성 방정식을 이용해서 계산해 보도록 하겠다.

게시글 (https://pasus.tistory.com/346)에 있는 가우스 행성 방정식은 다음과 같았다.

 

\[ \begin{align} & \frac{da}{dt}= \frac{2a^2}{h} e \sin \theta \ a_r+ \frac{2a^2}{h} (1+e \cos \theta ) \ a_\theta \tag{1} \\ \\ & \frac{de}{dt}= \frac{h}{\mu} \sin \theta \ a_r+ \frac{1}{h} \left[ \left( r+ \frac{h^2}{\mu} \right) \cos \theta +er \right] \ a_\theta \\ \\ & \frac{di}{dt}= \frac{r}{h} \cos (\omega + \theta) \ a_h \\ \\ & \frac{d\Omega}{dt} = \frac{r \sin (\omega + \theta) }{h \sin i } \ a_h \\ \\ & \frac{d \omega }{dt}= - \frac{h}{e \mu } \cos \theta \ a_r + \frac{1}{eh} \left( r+ \frac{h^2}{\mu} \right) \sin \theta \ a_\theta - \frac{r \sin (\omega + \theta ) }{h \tan i } \ a_h \\ \\ & \frac{d\theta}{dt}= \frac{h}{r^2} + \frac{h}{e \mu} \cos \theta \ a_r- \frac{1}{eh} \left(r+ \frac{h^2}{\mu} \right) \sin \theta \ a_\theta \\ \\ & \frac{dh}{dt}=r \ a_\theta \end{align} \]

 

여기서 \(a_r, \ a_\theta, \ a_h\) 는 LVLH(local-vertical-local-horizontal) 좌표계 \(\{o\}\) 로 표현된 섭동 가속도 벡터 \(\vec{a}_p\) 의 축 성분이다.

 

\[ \begin{align} \mathbf{a}_p^o= \begin{bmatrix} a_r \\ a_\theta \\ a_h \end{bmatrix} \tag{2} \end{align} \]

 

한편 게시글 (https://pasus.tistory.com/349)에 의하면 J2 섭동 가속도는 다음과 같이 ECI 죄표계 \(\{i\}\) 로 주어졌다.

 

\[ \begin{align} \mathbf{a}_p^i= \begin{bmatrix}a_x \\ a_y \\ a_z \end{bmatrix} = \frac{3}{2} J_2 \frac{\mu}{r^2} \left( \frac{R_e}{r} \right)^2 \begin{bmatrix} \frac{x}{r} \left(5 \left( \frac{z}{r} \right)^2-1 \right) \\ \frac{y}{r} \left(5 \left( \frac{z}{r} \right)^2-1 \right) \\ \frac{z}{r} \left(5 \left( \frac{z}{r} \right)^2-3 \right) \end{bmatrix} \tag{3} \end{align} \]

 

여기서 \(x, \ y, \ z\) 는 위치벡터 \(\vec{r}\) 을 ECI 좌표계로 표현한 축 성분이다.

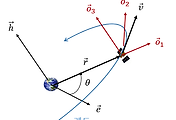
식 (1)과 (3)에 의하면 가우스 행성 방정식을 사용하려면 J2 섭동 가속도를 LVLH 좌표계로 변환해야 한다. ECI 좌표계 \(\{i\}\) 에서 LVLH 좌표계 \(\{o\}\) 로의 DCM \(C_o^i\) 는 다음과 같다.

 

\[ \begin{align} C_o^i &= C(z, \Omega)C(x, i)C(z, \omega+\theta) \tag{4} \\ \\ &= \begin{bmatrix} c \Omega \ c (\omega + \theta) - s \Omega \ c i \ s (\omega + \theta ) & -c \Omega \ s⁡ (\omega +\theta) - s \Omega \ c i \ c (\omega + \theta) & s \Omega \ s i \\ s \Omega \ c (\omega+ \theta) + c \Omega \ c i \ s (\omega + \theta ) & -s \Omega \ s (\omega + \theta) + c \Omega \ c i \ c (\omega + \theta ) & -c \Omega \ s i \\ s⁡ i \ s (\omega + \theta ) & s⁡ i \ c (\omega+ \theta) & c i \end{bmatrix} \end{align} \]

 

여기서 \(c= \cos , \ s= \sin \) 을 의미한다.

 

 

그러면 섭동 가속도는 다음과 같이 변환할 수 있다.

 

\[ \begin{align} & \mathbf{a}_p^o= \left(C_o^i \right)^T \mathbf{a}_p^i \tag{5} \\ \\ & \ \ \ \to \begin{bmatrix} a_r \\ a_\theta \\ a_h \end{bmatrix} = \begin{bmatrix} c \alpha \ c \phi \ a_x+ s \alpha \ c \phi \ a_y+ s \phi \ a_z \\-s \alpha \ a_x+c \alpha \ a_y \\ -c \alpha \ s \phi \ a_x-s \alpha \ s \phi \ a_y+ c \phi \ a_z \end{bmatrix} \end{align} \]

 

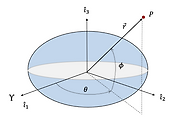
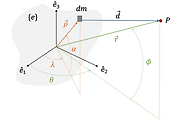
하지만 여기서 섭동 가속도를 좌표변환하기 전에 먼저 식 (3)의 섭동 가속도식에 있는 ECI 좌표계와 관련된 변수 \(x, y, z\) 를 LVLH 좌표계 변수와 관련된 궤도요소의 함수로 바꿔야 한다. 이를 위해서 임시 좌표계 \(\{t\}\) 를 도입한다. 임시 좌표계는 다음과 같이 ECI 좌표계의 z축을 중심으로 \(\alpha\) 만큼 회전한 후 다시 y축으로 \(-\phi\) 만큼 회전하여 얻어진 좌표계다. 따라서 임시 좌표계의 x축은 LVLH 좌표계의 x축과 일치한다.

 

 

그러면 ECI 좌표계에서 임시 좌표계로의 DCM \(C_t^i\) 는 다음과 같다.

 

\[ \begin{align} C_t^i &= C(z, \alpha) C(y, - \phi) \tag{6} \\ \\ &= \begin{bmatrix} c \alpha \ c \phi & -s \alpha & -c \alpha \ s \phi \\ s \alpha \ c \phi & c \alpha & -s \alpha \ s \phi \\ s \phi & 0 & c \phi \end{bmatrix} \end{align} \]

 

좌표변환을 이용하면 위치벡터 \(\vec{r}\) 은 다음과 같이 각각 임시 좌표계, LVLH 좌표계 및 ECI 좌표계로 표현할 수 있다.

 

\[ \begin{align} \mathbf{r}^o=\mathbf{r}^t=\begin{bmatrix} r \\ 0 \\ 0 \end{bmatrix}, \ \ \ \ \mathbf{r}^i=C_o^i \mathbf{r}^o=C_t^i \mathbf{r}^t \tag{7} \end{align} \]

 

따라서 식 (4), (6), (7)을 이용하면 다음과 같은 관계식을 얻을 수 있다.

 

\[ \begin{align} \frac{x}{r} &= \cos \alpha \cos \phi \tag{8} \\ \\ &= \cos \Omega \cos (\omega+ \theta)- \sin \Omega \cos i \sin (\omega+ \theta) \\ \\ \frac{y}{r} &= \sin \alpha \cos \phi \\ \\ &= \sin \Omega \cos (\omega + \theta)+ \cos \Omega \cos i \sin (\omega+\theta) \\ \\ \frac{z}{r} &= \sin \phi = \sin i \sin (\omega+ \theta) \end{align} \]

 

식 (8)을 식 (3)에 대입하면 J2 섭동 가속도는 다음과 같이 된다.

 

\[ \begin{align} \mathbf{a}_p^i= \frac{3}{2} J_2 \frac{\mu}{r^2} \left( \frac{R_e}{r} \right)^2 \begin{bmatrix} \cos \alpha \cos \phi \ (5 \sin^2 \phi-1) \\ \sin \alpha \cos \phi \ (5 \sin^2 \phi-1) \\ \sin \phi \ (5 \sin^2 \phi-3) \end{bmatrix} \tag{9} \end{align} \]

 

 

 

이제 식 (9)를 (5)에 대입하면 다음과 같이 LVLH 좌표계로 표현된 J2 섭동 가속도의 축 성분을 구할 수 있다.

 

\[ \begin{align} \tilde{a}_r &= (c \Omega \ c (\omega+ \theta)-s \Omega \ c i \ s (\omega+ \theta) ) \ a_x \tag{10} \\ & \ \ \ \ \ + (s \Omega \ c (\omega+\theta)+ c \Omega \ c i \ s (\omega+ \theta) ) \ a_y \\ & \ \ \ \ \ +(s i \ s (\omega+ \theta) ) \ a_z \\ \\ &= \cos \alpha \cos \phi \ a_x + \sin \alpha \cos \phi \ a_y+ \sin \phi \ a_z \\ \\ & = \cos^2 \alpha \cos^2 \phi \ (5 \sin^2 \phi-1)+ \sin^2 \alpha \cos^2 \phi \ (5 \sin^2 \phi-1) \\ & \ \ \ \ \ +\sin^2 \phi \ (5 \sin^2 \phi-3) \\ \\ & =(5 \sin^2 \phi-1)-2 \sin^2 \phi \\ \\ &=3 \sin^2 i \sin^2 (\omega + \theta)-1 \\ \\ \\ \tilde{a}_\theta &= (-c \Omega \ s (\omega+ \theta)- s \Omega \ c i \ c (\omega+ \theta) ) \ a_x \tag{11} \\ & \ \ \ \ \ + (-s \Omega \ s (\omega+ \theta)+c \Omega \ c i \ c (\omega+ \theta) ) \ a_y \\ & \ \ \ \ \ + (s i \ c (\omega+ \theta) ) \ a_z \\ \\ &= \begin{bmatrix} -c \Omega \ s (\omega+ \theta)-s \Omega \ c i \ c (\omega+ \theta) ) \cos \alpha \cos \phi \\ +(-s \Omega \ s (\omega+ \theta)+c \Omega \ c i \ c (\omega+\theta) ) \sin \alpha \cos \phi \\+s i \ c (\omega+ \theta) \sin \phi \end{bmatrix} \ (5 \sin^2 \phi-1) \\ & \ \ \ \ \ -2 \sin i \cos (\omega+ \theta) \sin \phi \\ \\ &= -2 \sin^2 i \sin (\omega+ \theta) \cos (\omega+\theta) \\ \\ &=-\sin^2 i \sin 2(\omega+\theta) \\ \\ \\ \tilde{a}_h & = s \Omega \ s i \ a_x- c \Omega \ s i \ a_y+c i \ a_z \tag{12} \\ \\ &= \sin \Omega \sin i \cos \alpha \cos \phi \ (5 \sin^2 \phi-1) \\ & \ \ \ \ \ -\cos \Omega \sin i \sin \alpha \cos \phi \ (5 \sin^2 \phi-1)+ \cos i \sin \phi \ (5 \sin^2 \phi-3) \\ \\ &= \begin{bmatrix} \sin \Omega \sin i \cos \alpha \cos \phi \\ - \cos \Omega \sin i \sin \alpha \cos \phi \\ +\cos i \sin \phi \end{bmatrix} \ (5 \sin^2 \phi-1)-2 \cos i \sin \phi \\ \\ &=-2 \cos i \sin \phi \\ \\ &=-\sin 2i \sin (\omega+ \theta) \end{align} \]

 

여기서 \(\tilde{a}_r, \tilde{a}_\theta, \tilde{a}_h\) 에 \( \frac{3}{2} J_2 \frac{\mu}{r^2} \left( \frac{R_e}{r} \right)^2\) 을 곱하면 \(a_r, a_\theta, a_h\) 을 얻을 수 있다. 또한 식 (8)을 이용하면 식 (11)과 (12)에 있는 대괄호 항은 \(0\) 이 됨을 보일 수 있다.

촤종적으로 가우스 행성 방정식 (1)에 식 (11), (12), (13)을 대입하고 전개하면 J2 섭동에 의한 궤도요소의 시간 변화율은 다음과 같다.

 

\[ \begin{align} \frac{da}{dt} & = 3J_2 \frac{a^2 \mu R_e^2 }{hr^4} \begin{bmatrix} e \sin \theta \ (3 \sin^2 i \sin^2 (\omega + \theta)-1) \\ -(1+e \cos \theta ) \sin^2 i \sin 2(\omega+ \theta) \end{bmatrix} \tag{13} \\ \\ \frac{de}{dt} &= \frac{3}{2} J_2 \frac{\mu R_e^2}{hr^3 } \begin{bmatrix} \frac{h^2}{\mu r} \sin \theta \ (3 \sin^2 i \sin^2 (\omega + \theta)-1) \\ -[ (2+e \cos \theta ) \cos \theta+e ] \sin^2 i \sin 2(\omega +\theta) \end{bmatrix} \\ \\ \frac{di}{dt} &= \frac{3}{2} J_2 \frac{\mu R_e^2}{ehr^3} \begin{bmatrix} \frac{h^2}{\mu r} \cos \theta \ (1-3 \sin^2 i \sin^2 (\omega+\theta) ) \\ -(2+e \cos \theta ) \ \sin \theta \sin^2 i \sin 2(\omega+\theta) \\ +2e \cos^2 i \sin^2 (\omega+ \theta) \end{bmatrix} \\ \\ \frac{d\Omega}{dt} &= -3 J_2 \frac{\mu R_e^2}{hr^3 } \cos i \sin^2 (\omega+\theta) \\ \\ \frac{d\omega }{dt} &= \frac{3}{2} J_2 \frac{\mu R_e^2}{ehr^3 } \begin{bmatrix} \frac{h^2}{\mu r} \cos \theta \ (1-3 \sin^2 i \sin^2 (\omega +\theta) ) \\ -(2+e \cos \theta ) \sin \theta \sin^2 i \sin 2(\omega +\theta) \\ +2e \cos^2 i \sin^2 (\omega+\theta) \end{bmatrix} \\ \\ \frac{d \theta}{dt} &= \frac{h}{r^2 }+ \frac{3}{2} J_2 \frac{\mu R_e^2}{ehr^3} \begin{bmatrix} \frac{h^2}{\mu r} \cos \theta \ (3 \sin^2 i \sin^2 (\omega + \theta)-1) \\ + (2+ e \cos \theta ) \sin \theta \sin^2 i \sin 2(\omega+\theta) \end{bmatrix} \\ \\ \frac{dh}{dt} &= - \frac{3}{2} J_2 \frac{\mu R_e^2}{r^3} \sin^2 i \sin 2(\omega+\theta) \end{align} \]