특이값 분해는 다음과 같이 어떤 \( m \times n \) 실수 행렬(real matrix) \( A \)를 3개의 행렬의 곱으로 분해한 것이다.
\[ A = U \Sigma V^T \tag{1} \]
이 식을 풀어 쓰면 다음과 같다.
\[ A = \sigma _1 \mathbf{u}_1 \mathbf{v}_1^T + \sigma _2 \mathbf{u}_2 \mathbf{v}_2^T + \cdots + \sigma _r \mathbf{u}_r \mathbf{v}_r^T \tag{2} \]
여기서 \( \sigma _i \)는 특이값으로서 그 숫자는 행렬 \( A \)의 랭크(rank)와 같다. 특이값은 큰 값에서 작은 값의 순서로 정렬시킨 것이다.
\[ \sigma _1 \ge \sigma _2 \ge \cdots \ge \sigma _r > 0 \tag{3} \]
\( \mathbf{u}_i \)와 \( \mathbf{v}_i \)는 각각 행렬 \( U \)와 \( V \)를 구성하는 열(column) 벡터로서 특이값 \( \sigma _i \)에 대응하는 단위 직교 벡터이다. \( \mathbf{u}_i \)는 \( m \times 1 \) 벡터며 \( \mathbf{v}_i \)는 \( n \times 1 \) 벡터다.
특이값 분해(svd)는 선형 대수학에서는 매우 중요한 개념이며 응용 범위가 상당히 넓다.
그런데 특이값 분해(svd)로 어떻게 이미지를 압축시킬 수 있다는 걸까. 힌트는 식 (2)에 있다.
식 (2)의 오른쪽 항은 \( r \)개의 행렬 \( \sigma _i \mathbf{u}_i \mathbf{v}_i^T \)의 합으로 되어 있다. 각각의 행렬은 특이값과 두 개 열벡터의 곱으로 이루어져 있으므로 각 행렬은 랭크가 1인 행렬이다. 따라서 식 (2)에 의하면 랭크가 \( r \)인 임의의 행렬 \( A \)는 랭크가 1인 \( r \)개의 행렬의 합으로 표현할 수 있다.
그렇다면 행렬 \( A \)를 랭크가 1인 행렬로 근사화하고 싶다면 어떻게 하면 좋을까. 특이값은 큰 수부터 작은 수로 정렬되어 있으므로 가장 큰 특이값을 갖는 다음 행렬로 근사하면 될 것이다.
\[ A \approx \sigma _1 \mathbf{u}_1 \mathbf{v}_1^T \tag{4} \]
그렇다면 랭크가 5인 행렬로 근사하고 싶다면? 다음과 같이 특이값 5개를 사용하면 될 것이다.
\[ A \approx \sigma _1 \mathbf{u}_1 \mathbf{v}_1^T + \cdots + \sigma _5 \mathbf{u}_5 \mathbf{v}_5^T \tag{5} \]
행렬로 표현할 수 있는 데이터 중에서 가장 대표적인 것이 디지털 이미지다. 디지털 이미지는 픽셀의 강도(intensity)를 성분 값으로 하는 행렬이다. 다음 이미지를 보자. 유명한 레나의 흑백 사진이다.

레나 이미지는 \( 512 \times 512 \) 행렬로 되어 있고, 행렬의 성분을 보면 다음과 같이 0부터 1사이의 숫자로 되어 있다.
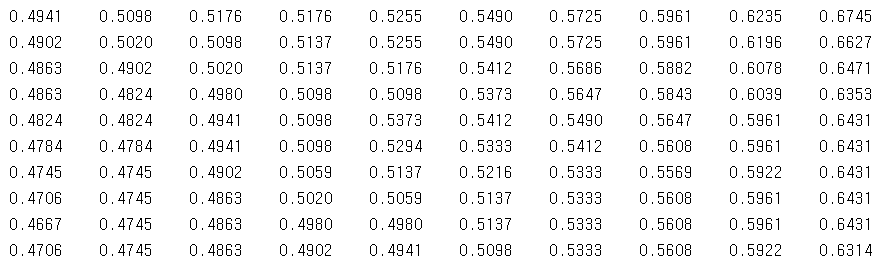
즉, 레나 이미지를 표현하기 위해서는 \( 512 \times 512 = 262,144 \)개의 픽셀 값이 필요하다. 물론 데이터의 용량이 크다고는 할 수 없지만 이런 이미지가 수 만개라면 또는 1초에 30 프레임의 동영상이라면 이야기가 달라진다. 레나 이미지 행렬을 특이값을 계산해 보면 .
\[ 254.0067,\ 41.6316,32.\ 1130,25. \ 4434,23. \ 1194, \ \cdots \ , \ 0.0001, \ 0.0001 \]
등 \( 512 \)개의 값이 나온다. 레나 이미지 행렬의 랭크는 \( 512 \)라는 이야기이다. 특이값을 그래프로 보면 다음과 같다.
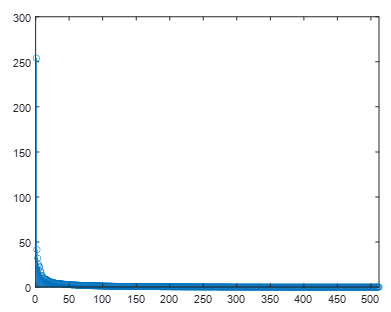
너무 복잡하므로 앞에서 20개 정도만 그려보면 다음과 같다.
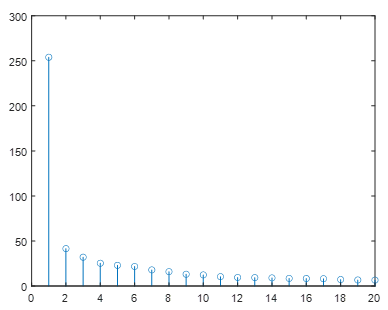
첫번째 특이값만 크고 그 다음부터는 고만고만 한 것 같다. 그렇다면 레나 이미지 행렬을 랭크 1인 행렬로 근사화해 보자. 이미지 질만 확보된다면 엄청난 이미지 압축률을 보일 것이다. 왜냐하면 \( 512+512=1,024 \)개의 행렬 성분 값만 있으면 되기 때문에 \( 1,024/262,144 = 0.0039 \), 즉 원래 데이터 수의 0.39% 만 가지고 이미지를 표시할 수 있다. 해보자.

뭐가 뭔지 모르게 나왔다. 조금 더 써보자. 이번에는 레나 이미지 행렬을 랭크 20인 행렬로 근사화해 보자. 이 정도 해도 \( (1,024 \times 20) / 262,144 = 0.0781\), 즉 원래 데이터 수의 7.81% 만 가지고 이미지를 표시할 수 있다.

이제 누구인지 구별은 할 수 있으나 이미지 질이 좋지 않다. 다시 레나 이미지 행렬을 랭크 100인 행렬로 근사화해 보자. 그러면 \( (1,024 \times 100) / 262,144 = 0.3906 \), 즉 원래 데이터 수의 39.06% 만 가지고 이미지를 표시할 수 있다.

원본과 비교해보면 차이를 못 느낄 정도가 됐다. 이 이미지는 원본 데이터 수의 39.06 % 만 가지고 표시한 것이다.
특이값 분해(svd)를 이용하면 이미지 뿐만 아니라 행렬로 표현할 수 있는 많은 종류의 데이터를 압축할 수 있다.
'AI 수학 > 선형대수' 카테고리의 다른 글
| 내적 (Inner Product) (0) | 2020.10.21 |
|---|---|
| 유사 역행렬 (Pseudo Inverse Matrix) (0) | 2020.10.19 |
| 특이값 분해(SVD)의 증명 (0) | 2020.07.23 |
| 특이값 분해(singular value decomposition) (0) | 2020.07.23 |
| 정정(positive-definite) 행렬의 고유값 (0) | 2020.07.21 |




댓글