벨만 방정식을 이용하여 이산시간(discrete-time) LQR을 유도해 보도록 하자. 여기서 마르코프 결정 프로세스(MDP)는 결정적(deterministic) 프로세스로 가정한다.
결정적 프로세스이므로, 특정 상태변수에서 행동이 정해지면 다음(next) 상태변수를 확정적으로 계산할 수 있다. 환경 모델은 다음과 같이 표현된다.
\[ \mathbf{x}_{t+1}=A \mathbf{x}_t+B \mathbf{u}_t \tag{1} \]
보상(reward)도 확률변수가 아닌 확정된 값으로 주어지며 다음과 같이 정의한다.
\[ r(\mathbf{x}_t, \mathbf{u}_t)= -\frac{1}{2} \left( \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{u}_t^T R \mathbf{u}_t \right) \ \tag{2} \]
여기서 \(Q=Q^T \ge 0\), \(R=R^T \gt 0\) 이다. 그러면 상태가치 함수는 다음과 같이 된다.
\[ V^\pi (\mathbf{x}_t)= -\frac{1}{2} \sum_{k=t}^\infty \left( \mathbf{x}_k^T Q \mathbf{x}_k+ \mathbf{u}_k^T R \mathbf{u}_k \right) \ \tag{3} \]
참고로 확정적 정책에서는 행동가치 함수와 상태가치 함수는 동일하다. 여기서 보상과 상태가치 함수를 음수로 정의한 이유는, 강화학습에서는 상태가치 값을 최대로 하는 정책을 찾는 반면, 최적제어에서는 비용함수(cost function)를 최소로 하는 제어법칙을 찾기 때문이다. 식 (3)은 이산시간 LQR의 목적함수와 동일하다.
상태가치 함수의 정의에서 감가율(discount factor)을 \(\gamma=1\) 로 정했기 때문에 상태가치 함수가 유한한 값을 갖기 위해서는 시스템을 안정화(stable)시키는 정책을 찾아야 한다. 위 식을 한 시간스텝 전개하면,
\[ \begin{align} V^\pi (\mathbf{x}_t) &= -\frac{1}{2} \left( \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{u}_t^T R \mathbf{u}_t \right) -\frac{1}{2} \sum_{k=t+1}^\infty \left( \mathbf{x}_k^T Q \mathbf{x}_k+ \mathbf{u}_k^T R \mathbf{u}_k \right) \tag{4} \\ \\ &= -\frac{1}{2} \left( \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{u}_t^T R \mathbf{u}_t \right) + V^\pi (\mathbf{x}_{t+1}) \end{align} \]
으로 이산시간 LQR에 대한 벨만 방정식이 된다.
상태가치 함수가 다음과 같이 상태변수의 제곱 함수 형태로 계산된다고 가정한다면,
\[ V^\pi (\mathbf{x}_t)= -\frac{1}{2} \mathbf{x}_t^T P \mathbf{x}_t \tag{5} \]
벨만 방정식 (4)는
\[ \begin{align} 2V^\pi (\mathbf{x}_t) &= - \left( \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{u}_t^T R \mathbf{u}_t \right) + 2 V^\pi (\mathbf{x}_{t+1}) \tag{6} \\ \\ &= - \left( \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{u}_t^T R \mathbf{u}_t \right) - (A \mathbf{x}_t+B \mathbf{u}_t)^T P (A \mathbf{x}_t + B \mathbf{u}_t) \end{align} \]
이 된다. 여기서 \(P=P^T \gt 0\) 이다. 그리고 결정적 정책으로서 상태 피드백(state-feedback) 정책
\[ \mathbf{u}_t=\pi (\mathbf{x}_t )=K \mathbf{x}_t \tag{7} \]
를 사용한다고 가정하면, 식 (6)은
\[ \begin{align} 2V^\pi (\mathbf{x}_t) &= - \mathbf{x}_t^T P \mathbf{x}_t \tag{8} \\ \\ &= - \left( \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{x}_t^T K^T RK \mathbf{x}_t \right) - \mathbf{x}_t^T ( A+BK)^T P (A+BK) \mathbf{x}_t \end{align} \]
이 되어, 다음과 같은 리야프노프 방정식(Lyapunov equation)을 유도할 수 있다.
\[ (A+BK)^T P(A+BK)+Q+K^T RK-P=0 \tag{9} \]
즉, 이산시간 LQR에 대한 벨만 방정식은 리야프노프 방정식과 동일하다. 감가율이 \(\gamma=1\) 이므로 피드백 시스템을 안정화(stable)시키는 게인 \(K\) 를 선정해야 한다.
이제 정책 이터레이션을 이산시간 LQR에 적용해 보도록 한다. LQR에 대한 벨만 방정식 (4)를 풀기 위해 정책 이터레이션의 정책 평가 단계를 적용하면 다음과 같다.
\[ V_{j+1} (\mathbf{x}_t ) \gets -\frac{1}{2} \left( \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{u}_t^T R \mathbf{u}_t \right)+V_j (\mathbf{x}_{t+1} ) \tag{10} \]
여기서 아래 첨자 \(j\) 는 가치함수의 계산 반복 횟수를 나타낸다. 상태가치 함수가 식 (5)와 같이 상태변수의 제곱 함수 형태로 계산된다고 가정했으므로
\[ \mathbf{x}_t^T P_{j+1} \mathbf{x}_t \gets \mathbf{x}_t^T Q \mathbf{x}_t+ \mathbf{u}_t^T R \mathbf{u}_t +\mathbf{x}_{t+1}^T P_j \mathbf{x}_{t+1} \tag{11} \]
이 된다. 또한 상태 피드백(state-feedback) 정책, \(\mathbf{u}_t=K\mathbf{x}_t\) 를 사용한다고 가정했으므로, 식 (11)에 대입하면 다음과 같은 리야프노프 방정식의 재귀식 형태를 유도할 수 있다.
\[ P_{j+1} \gets (A+BK)^T P_j (A+BK)+Q+K^T RK \tag{12} \]
위 식을 수렴할 때까지 반복하여 계산한다.

그리고 다음 식으로 정책 개선을 수행한다.
\[ \begin{align} \pi_{i+1} (\mathbf{x}_t ) &= K_{i+1} \mathbf{x}_t \tag{13} \\ \\ &= \arg\max_{\mathbf{u}_t } \left( -\mathbf{x}_t^T Q \mathbf{x}_t- \mathbf{u}_t^T R \mathbf{u}_t- \mathbf{x}_{t+1}^T P \mathbf{x}_{t+1} \right) \end{align} \]
여기서 \(P\) 는 리야프노프 재귀 방정식 (12)의 수렴된 해이다. 위 식에서 오른쪽 항을 최대로 만드는 \(\mathbf{u}_t\) 를 구하기 위하여 다음과 같이 미분을 수행한다.
\[ \begin{align} 0 &= \frac{\partial}{\partial \mathbf{u}_t} \left( -\mathbf{x}_t^T Q \mathbf{x}_t- \mathbf{u}_t^T R \mathbf{u}_t- (A \mathbf{x}_t+B\mathbf{u}_t)^T P (A \mathbf{x}_t+B\mathbf{u}_t) \right) \tag{14} \\ \\ &= R \mathbf{u}_t+ B^T P (A \mathbf{x}_t+B\mathbf{u}_t) \end{align} \]
식 (14)에서 다음과 같이 개선된 정책을 계산할 수 있다.
\[ \mathbf{u}_t= K_{i+1} \mathbf{x}_t= - (B^T PB+R)^{-1} B^T PA \mathbf{x}_t \tag{15} \]
또는 다음과 같이 업데이트된 피드백 게인을 계산할 수 있다.
\[ K_{i+1}=-(B^T PB+R)^{-1} B^T PA \tag{16} \]
다시 새로운 정책 식 (15) 또는 (16)에 대해서 정책 평가를 식 (12)를 이용하여 실시하고 이를 이용하여 더 개선된 정책을 계산하는 프로세스를 되풀이한다.
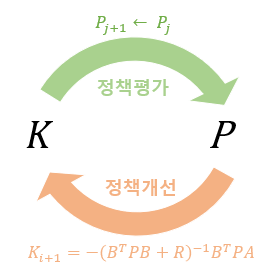
여기서 주의할 점은 초기 정책에 의한 게인, 즉 \(K_0\) 는 시스템을 안정화(stable)시키는 게인이어야 한다는 것이다.
정책 이터레이션으로 얻어지는 LQR 알고리즘을 Hewer 알고리즘이라고 한다. 이 알고리즘은 시스템 운동 방정식 또는 환경의 운동 방정식, 즉 \((A, B)\) 를 정확히 알아야 수행 가능하다. 만약 모른다면? 모델프리(model free)강화학습 기반 LQR에 대해서는 다음에 ...
'AI 딥러닝 > RL' 카테고리의 다른 글
| Tensorflow2로 만든 DDPG 코드: BipedalWalker-v3 (0) | 2021.07.09 |
|---|---|
| 가치 이터레이션 (Value Iteration)과 LQR (0) | 2021.06.23 |
| Tensorflow2로 만든 SAC 코드: Pendulum-v0 (0) | 2021.06.01 |
| Soft Actor Critic (SAC) 알고리즘 - 2 (0) | 2021.05.30 |
| Soft Actor Critic (SAC) 알고리즘 - 1 (0) | 2021.05.29 |




댓글