어떤 정책 \(\pi\) 에 대해서 행동가치 함수가 주어지면 기존의 정책 보다 더 큰 상태가치 또는 행동가치 값을 갖는 새로운 정책 \(\pi^\prime\) 을 계산할 수 있다. 이 과정을 정책 개선(policy improvement)이라고 한다.
새로운 정책은 다음과 같이 탐욕(greedy)적인 방법으로 찾을 수 있다.
\[ \pi^\prime = \arg \max_{\mathbf{u}_t} Q^\pi (\mathbf{x}_t, \mathbf{u}_t) \tag{1} \]
여기서 탐욕적이라는 의미는 먼 미래 대신에 한 시간스텝만을 고려하여 최대값을 구한다는 것을 말한다. 탐욕적 방법으로 새로운 정책을 계산하면 확정적(deterministic) 정책이 된다.
\[ \mathbf{u}_t= \pi^\prime (\mathbf{x}_t) \tag{2} \]
위와 같은 방법으로 새로운 정책을 구하고 이 정책에 대하여 상태가치 함수를 계산하면, \(V^{\pi^\prime} (\mathbf{x}_t ) \ge V^\pi (\mathbf{x}_t)\) 가 된다. 증명해 보자.
증명은 행동가치 함수와 상태가치 함수의 관계식에서 출발한다.
\[ \begin{align} V^\pi (\mathbf{x}_t ) & = \int_{\mathbf{u}_t} Q^\pi (\mathbf{x}_t, \mathbf{u}_t ) \pi(\mathbf{u}_t | \mathbf{x}_t ) d\mathbf{u}_t \tag{3} \\ \\ & \le \max_{\mathbf{u}_t} Q^\pi (\mathbf{x}_t, \mathbf{u}_t ) \int_{\mathbf{u}_t} \pi(\mathbf{u}_t | \mathbf{x}_t ) d \mathbf{u}_t \\ \\ & = \max_{\mathbf{u}_t } Q^\pi (\mathbf{x}_t, \mathbf{u}_t ) \end{align} \]
한편 행동가치 함수와 상태가치 함수의 또 다른 관계식으로부터,
\[ Q^\pi (\mathbf{x}_t, \mathbf{u}_t ) = r(\mathbf{x}_t, \mathbf{u}_t)+ \mathbb{E}_{\mathbf{x}_{t+1} \sim p(\mathbf{x}_{t+1} \vert \mathbf{x}_t, \mathbf{u}_t ) } \left[ \gamma V^\pi (\mathbf{x}_{t+1} ) \right] \tag{4} \]
이 성립하므로, 식 (1)을 이용하면 식 (4)의 최대값은 다음과 같이 된다.
\[ \begin{align} \max_{\mathbf{u}_t} Q^\pi (\mathbf{x}_t, \mathbf{u}_t ) & = r(\mathbf{x}_t, \pi'(\mathbf{x}_t)) \tag{5} \\ & \ \ \ \ \ + \mathbb{E}_{\mathbf{x}_{t+1} \sim p(\mathbf{x}_{t+1} \vert \mathbf{x}_t, \pi'(\mathbf{x}_t )) } \left[ \gamma V^{\pi'} (\mathbf{x}_{t+1} ) \right] \end{align} \]
식 (6)으로 주어지는 상태가치 함수에 관한 벨만 방정식에서 \(\pi\) 대신에 \(\pi'\) 을 대입하면
\[ V^\pi (\mathbf{x}_t ) = \mathbb{E}_{ \mathbf{u}_t \sim \pi(\mathbf{u}_t \vert \mathbf{x}_t ) } \left[ r_t+ \mathbb{E}_{\mathbf{x}_{t+1} \sim p(\mathbf{x}_{t+1} \vert \mathbf{x}_t, \mathbf{u}_t) } \left[ \gamma V^\pi (\mathbf{x}_{t+1} ) \right] \right] \tag{6} \]
위 식은 다음과 같이 되어서 식 (5)와 일치한다.
\[ \begin{align} V^{\pi'} (\mathbf{x}_t ) &= r (\mathbf{x}_t, \pi'(\mathbf{x}_t)) + \mathbb{E}_{\mathbf{x}_{t+1} \sim p(\mathbf{x}_{t+1} \vert \mathbf{x}_t, \pi'(\mathbf{x}_t)) } \left[ \gamma V^{\pi'} (\mathbf{x}_{t+1} ) \right] \tag{7} \\ \\ &= \max_{\mathbf{u}_t} Q^\pi (\mathbf{x}_t, \mathbf{u}_t) \end{align} \]
식 (7)에서 기댓값 \( \mathbb{E}_{ \mathbf{u}_t \sim \pi(\mathbf{u}_t \vert \mathbf{x}_t ) } [ \ ]\) 이 사라진 이유는 \(\pi'\) 이 확정적 정책이기 때문이다. 식 (3)과 (7) 에 의해서 다음 관계식이 성립한다.
\[ V^\pi (\mathbf{x}_t ) \le V^{\pi^\prime} (\mathbf{x}_t ) \tag{8} \]
따라서 정책 개선이 증명되었다.

한편 임의의 정책 \(\pi\) 가 주어지면, 상태가치 함수 또는 행동가치 함수에 대한 벨만 방정식을 풀어서 상태가치 또는 행동가치를 계산할 수 있다. 이 과정을 정책 평가(policy evaluation)라고 한다.
상태가치 함수와 행동가치 함수에 대한 벨만 방정식은 각각 다음과 같았다.
\[ \begin{align} & V^\pi (\mathbf{x}_t )= \mathbb{E}_{ \mathbf{u}_t \sim \pi (\mathbf{u}_t | \mathbf{x}_t ) } \left[ r_t + \mathbb{E}_{ \mathbf{x}_{t+1} \sim p (\mathbf{x}_{t+1} | \mathbf{x}_t , \mathbf{u}_t) } \left[ \gamma V^\pi (\mathbf{x}_{t+1} ) \right] \right] \tag{9} \\ \\ & Q^\pi (\mathbf{x}_t, \mathbf{u}_t )= r_t + \mathbb{E}_{ \mathbf{x}_{t+1} \sim p (\mathbf{x}_{t+1} | \mathbf{x}_t , \mathbf{u}_t) } \left[ \mathbb{E}_{ \mathbf{u}_{t+1} \sim \pi (\mathbf{u}_{t+1} | \mathbf{x}_{t+1} ) } \left[ \gamma Q^\pi (\mathbf{x}_{t+1}, \mathbf{u}_{t+1} ) \right] \right] \end{align} \]
벨만 방정식은 보통 해석적인 해를 구할 수 없으므로 반복적 계산 방법, 즉 이터레이션(iteration) 방법으로 해를 구할 수 있다. 확정적 정책을 가정하고 벨만 방정식을 이터레이션 방법으로 풀면 다음과 같다.
\[ \begin{align} & V^\pi_{j+1} (\mathbf{x}_t )= r_t + \mathbb{E}_{ \mathbf{x}_{t+1} \sim p (\mathbf{x}_{t+1} | \mathbf{x}_t , \mathbf{u}_t) } \left[ \gamma V^\pi_j (\mathbf{x}_{t+1} ) \right] \tag{10} \\ \\ & Q^\pi_{j+1} (\mathbf{x}_t, \mathbf{u}_t )= r_t + \mathbb{E}_{ \mathbf{x}_{t+1} \sim p (\mathbf{x}_{t+1} | \mathbf{x}_t , \mathbf{u}_t) } \left[ \gamma Q^\pi_j (\mathbf{x}_{t+1}, \mathbf{u}_{t+1} ) \right] \end{align} \]
여기서 아래 첨자 \(j\)는 가치함수의 계산 반복 횟수를 나타낸다. 계산은 가치함수가 수렴할 때까지 반복한다.

가치함수가 수렴하면 임의의 정책 \(\pi_i\) 에 대해서 가치함수를 계산한 것이므로, 정책 개선(policy improvement)을 수행한다면 기존의 정책 보다 더 큰 가치함수 값을 갖는 새로운 정책 \(\pi_{i+1}\) 을 계산할 수 있다.
\[ \pi_{i+1} = \arg \max_{\mathbf{u}_t} Q^{\pi_i} ( \mathbf{x}_t, \mathbf{u}_t) \tag{11} \]
다시 새로운 정책 \(\pi_{i+1}\) 에 대해서 정책 평가를 실시하고, 이를 이용하여 다시 더 개선된 정책 \(\pi_{i+2}\) 를 산출할 수 있다. 이러한 프로세스를 정책 또는 가치함수가 수렴할 때까지 반복한다. 이와 같이 정책 평가와 정책 개선을 반복적으로 사용하는 프로세스를 정책 이터레이션(policy iteration)이라고 한다.
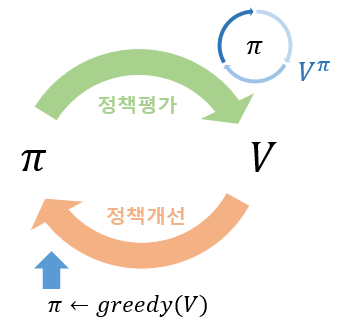
그렇다면 정책 이터레이션은 과연 특정한 정책과 가치함수로 수렴할까. 수렴한다면 그 정책은 모든 정책 중에서 가치함수를 최대로 만드는 정책이기 때문에 최적 정책(optimal policy)이라고 하고 그 때의 가치함수를 최적 가치함수라고 한다.
\[ \begin{align} & V^\star = \max_\pi V^\pi (\mathbf{x}_t) \tag{12} \\ \\ & Q^\star = \max_\pi Q^\pi (\mathbf{x}_t, \mathbf{u}_t) \\ \\ & \pi^\star (\mathbf{x}_t) = \arg \max_{\mathbf{u}_t} Q^\star (\mathbf{x}_t, \mathbf{u}_t) \end{align} \]
정책 이터레이션의 수렴에 관한 증명은 가치 이터레이션의 증명과 동일하므로 가치 이터레이션 설명 이후에 증명하도록 한다.
'AI 딥러닝 > RL' 카테고리의 다른 글
| 가치 이터레이션에서 Q-러닝으로 (0) | 2021.05.01 |
|---|---|
| 가치 이터레이션 (Value Iteration) (0) | 2021.04.29 |
| 벨만 최적 방정식 (Bellman Optimality Equation) (0) | 2021.04.28 |
| 강화학습에서의 이산공간과 연속공간 문제 (0) | 2021.04.26 |
| 가치함수 (Value Function) (0) | 2021.04.21 |




댓글