어떤 함수 \(y=f(x)\)의 조건수(condition number)는 함수의 입력인 \(x\)의 작은 변화울에 대해 함수의 출력인 \(y\)의 변화율이 얼마인지를 나타내는 수로서, 함수의 민감도를 측정하는 지표이다. 행렬의 조건수도 일반 함수의 조건수 정의를 이용하여 유도할 수 있다.
다음과 같이 행렬 \(A \in \mathbb{R}^{n \times n}\)와 어떤 벡터 \( \mathbf{b} \in \mathbb{R}^n\)에 관한 방정식이 있다고 하자.
\[ A \mathbf{x}= \mathbf{b} \]
여기서 벡터 \(\mathbf{b}\)가 어떤 작은 오차로 인하여 \(\mathbf{b}+\Delta \mathbf{b}\)로 변화했다면 이 방정식의 해 \(\mathbf{x}\)도 \(\mathbf{x}+\Delta \mathbf{x}\)로 변화할 것이다.
\[ A (\mathbf{x} +\Delta \mathbf{x})= \mathbf{b} + \Delta \mathbf{b} \]
이 식으로부터 \( A \Delta \mathbf{x}= \Delta \mathbf{b} \)의 관계식을 얻을 수 있고, 해의 변화량을 \(\Delta \mathbf{x} = A^{-1} \Delta \mathbf{b}\)로 계산할 수 있다. \(\Delta \mathbf{x}\)는 \(A^{-1}\)에 따라서 \(\Delta \mathbf{b}\)의 영향이 증폭되어 나타나기도 하고 반대로 축소되어 나타나기도 할 것이다.
벡터와 행렬의 크기를 놈(norm)으로 나타낸다면 오차의 크기는 다음 식으로 주어진다.
\[ \lVert \Delta \mathbf{x} \rVert \le \lVert A^{-1} \rVert \lVert \Delta \mathbf{b} \rVert \]
여기서 놈(norm)은 어떤 놈이라도 상관없다. 한편, 원래 식에서 벡터 \(\mathbf{b}\)와 해 \(\mathbf{x}\)의 크기 관계식은 다음과 같이 계산할 수 있다.
\[ \lVert \mathbf{b} \rVert = \lVert A \mathbf{x} \rVert \le \lVert A \rVert \lVert \mathbf{x} \rVert \]
위 두 식을 각각 좌변과 우변끼리 곱하면 다음과 같이 된다.
\[ \lVert \Delta \mathbf{x} \rVert \lVert \mathbf{b} \rVert \le \lVert A^{-1} \rVert \lVert \Delta \mathbf{b} \rVert \lVert A \rVert \lVert \mathbf{x} \rVert \]
위 식으로부터 오차의 상대적인 변화율을 계산할 수 있다.
\[ \frac{ \lVert \Delta \mathbf{x} \rVert }{ \lVert \mathbf{x} \rVert } \le \lVert A \rVert \lVert A^{-1} \rVert \frac{ \lVert \Delta \mathbf{b} \rVert }{ \lVert \mathbf{b} \rVert } \]
따라서 입력의 상대 오차 \( \frac{ \lVert \Delta \mathbf{b} \rVert }{ \lVert \mathbf{b} \rVert } \)에 대한 해의 상대 오차 \( \frac{ \lVert \Delta \mathbf{x} \rVert }{ \lVert \mathbf{x} \rVert } \)는 \( \lVert A \rVert \lVert A^{-1} \rVert \)의 값에 의해 크기가 제한되는 것을 알 수 있다.
여기서 행렬 \(A\)의 조건수(condition number)를 다음과 같이 정의한다.
\[ c(A)= \lVert A \rVert \lVert A^{-1} \rVert \]
행렬 \(A\)의 조건수가 크면 일정한 크기의 입력의 상대 오차에 대해서 해의 상대 오차가 커질 수 있고 (ill-conditioned라고 한다), 반대로 작으면 해의 상대 오차도 작아지는 것을 알 수 있다(well-conditioned라고 한다). 따라서 행렬의 조건수는 방정식 \(A\mathbf{x}=\mathbf{b}\)의 민감도를 나타내는 지표라고 할 수 있다.
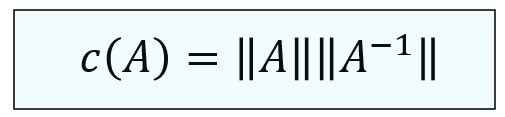
행렬의 조건수는 벡터 \(\mathbf{b}\) 대신에 행렬 \(A\)에 오차가 있을 때에도 나타난다.
\[ (A+ \Delta A) (\mathbf{x} + \Delta \mathbf{x})=\mathbf{b} \]
위 식을 전개하면
\[ A \mathbf{x} + A \Delta \mathbf{x} + \Delta A \mathbf{x} + \Delta A \Delta \mathbf{x}=\mathbf{b} \]
가 되는데 양변에 \(A^{-1}\)를 곱하고 놈(norm)을 씌우면 다음과 같이 된다.
\[ \begin{align} \lVert \Delta \mathbf{x} \rVert & \le \lVert A^{-1} \rVert \lVert \Delta A \rVert \lVert \mathbf{x} + \Delta \mathbf{x} \rVert \\ \\ &= c(A) \frac{ \lVert \Delta A \rVert }{ \lVert A \rVert } \lVert \mathbf{x} + \Delta \mathbf{x} \rVert \end{align} \]
또는
\[ \frac{ \lVert \mathbf{x} \rVert }{ \lVert \mathbf{x} + \Delta \mathbf{x} \rVert } \le c(A) \frac{ \lVert \Delta A \rVert }{ \lVert A \rVert } \]
따라서 조건수 \(c(A)\)는 행렬에 오차가 있을 때에도 해의 상대 오차의 크기에 영향을 미치는 것을 알 수 있다.
행렬 \(A\)의 조건수의 최소값은 \(1\)이다. 이유는 다음과 같다.
\[ c(A)= \lVert A \rVert \lVert A^{-1} \rVert \ge \lVert A A^{-1} \rVert = 1 \]
역행렬이 존재하지 않을 때(특이 행렬일 때) 조건수는 \(c(A)=\infty\)이다. 이유는 다음과 같다. 우선\( \lVert A^{-1} \rVert \ge \frac{1}{ \lVert A \rVert } \)로부터 조건수는 다음 식을 만족한다.
\[ c(A)= \lVert A \rVert \lVert A^{-1} \rVert = \left( \max \frac{ \lVert A \mathbf{x} \rVert }{ \lVert \mathbf{x} \rVert } \right) \left( \min \frac{ \lVert A \mathbf{x} \rVert }{ \lVert \mathbf{x} \rVert } \right)^{-1} \]
여기서 특이 행렬일 경우 \(\mathbf{x} \ne 0\)일 때 \(A \mathbf{x} = 0 \)이 가능하므로 \( \min \frac{ \lVert A \mathbf{x} \rVert }{ \lVert \mathbf{x} \rVert }=0 \)이기 때문에 \(c(A)=\infty\)가 된다.
행렬 \(A\)의 조건수의 정의에 의하면 조건수는 행렬 놈(norm)으로 어떤 놈을 사용하는 가에 따라 그 값이 달라진다. 가령 2-놈을 사용한다면 놈의 정의가 다음과 같으므로
\[ \lVert A \rVert = \max \frac{ \lVert A \mathbf{x}\rVert_2 }{ \lVert \mathbf{x} \rVert_2 } = \sqrt{\lambda_{max} (A^TA)} = \sigma_{max} \]
\(c(A)\)는 다음과 같이 계산된다.
\[ c(A)= \lVert A \rVert \lVert A^{-1} \rVert = \frac{\sigma_{max}}{ \sigma_{min}} \]
여기서 \(\lambda \)는 고유값 \(\sigma\)는 특이값을 의미한다. 예를 들어
\[ A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \]
일 경우에는 최대 특이값과 최소 특이값이 각각 \(5.465\), \(0.366\) 이므로 \(c(A)=14.932\)가 된다.
참고한 책
'AI 수학 > 선형대수' 카테고리의 다른 글
| 좌(왼쪽) 고유벡터 (left eigenvector) (0) | 2023.02.10 |
|---|---|
| Frobenius Norm 최소화 문제 (0) | 2022.11.03 |
| 놈 (norm) (0) | 2020.10.24 |
| 내적 (Inner Product) (0) | 2020.10.21 |
| 유사 역행렬 (Pseudo Inverse Matrix) (0) | 2020.10.19 |




댓글