사건 \(B\)가 발생한다는 가정(또는 조건)하에서 사건 \(A\)가 발생할 확률을 사건 \(A\)의 조건부 확률(conditional probability)이라고 하고, 다음과 같이 정의한다.
\[ P\{A|B \}=\frac{P\{A,B \}}{P \{B \}} \]
비슷하게 사건 \(A \)가 발생한다는 가정하에서 사건 \(B\)가 발생할 확률은 다음과 같이 쓸 수 있다.
\[ P\{B|A\}= \frac{P\{A,B\} }{ P\{A\} } \]
위 두 식을 이용하면 다음과 같은 연쇄법칙(chain rule)을 만들 수 있다.
\[ P\{A,B \} = P\{A│B \}P\{B\}=A\{B│A\}P \{A \} \]
한편 다음 그림과 같이 \( N \)개의 사건 \( \{ B_i, \ i=1,...,n \} \)이 서로 배타적이고 (즉, \( P\{B_i, B_j \}=0,\forall i \ne j \) ), 표본 공간을 모두 망라(exhaustive)하면 (즉 \( \sum_{i=1}^n P \{B_i\}=1 \) ),
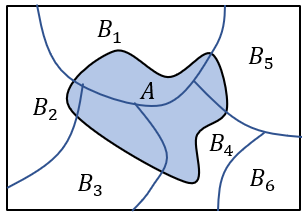
임의의 사건 \( A \)의 확률을 다음과 같이 표현할 수 있다.
\[ P\{A\}= \sum_{i=1}^n P\{A,B_i\}=\sum_{i=1}^n P \{A│B_i \} P\{B_i\} \]
위 식을 전확률(total probability) 정리라고 한다.
한편, 사건 \(A \)를 조건으로 하는 임의의 사건 \(B_i \)의 조건부 확률을 연쇄법칙을 이용해서 표현하면 다음과 같다.
\[ \begin{align} P\{B_i |A \} &= \frac{P\{A,B_i \}}{ P\{A\}} \\ \\ &= \frac{ P\{A|B_i \} P\{B_i\}}{ P\{A\} } \end{align} \]
위 식에 전확률 정리를 대입하면 다음과 같이 된다.
\[ P\{B_i |A \} = \frac{ P\{A|B_i \} P\{B_i\} }{ \sum_{i=1}^n P\{A|B_i \} P\{B_i \} } \]
위 식을 베이즈 정리(Bayes’theorem)이라고 한다. 여기서 \( P\{B_i\} \)를 사전(prior) 확률, \( P\{A|B_i \} \)를 빈도(likelihood) 확률, \( P\{B_i |A \} \)를 사후(posterior) 확률, \( \sum_{i=1}^n P\{A|B_i \} P\{B_i\} \)를 정규화 항이라고 한다.
베이즈 정리를 확률밀도함수의 식으로 표현하면 다음과 같다.
\[ \begin{align} p_{X|Y} (x│y) & = \frac{p_{Y|X} (y│x) p_X (x) } {(p_Y (y) } \\ \\ &= \frac{ p_{Y|X} (y│x) p_X (x) }{ \int_{-\infty}^{\infty} p_{Y|X} (y│x) p_X (x) dx } \end{align} \]
베이즈 정리는 공학뿐만 아니라 의학, 경제/경영학에서도 폭넓게 쓰이는 중요한 규칙이다.
베이즈 정리는 칼만필터와 파티클필터를 비롯한 대부분의 정적/동적 시스템에 대한 상태변수 추정 알고리즘의 근간을 이룬다. 기계학습(machine learning)에서는 주어진 데이터셋에 대한 최적의 파라미터나 모델을 찾는데 이용되고 있으며, 경제/경영학에서도 측정된 성과를 바탕으로 전략적인 결정을 개선하는데 활용된다.
베이즈 정리를 이용할 때는 보통 사건 \( B_i \)를 어떤 문제에 대한 가설 또는 모델로 보고, 사건 \( A \)는 이와 관련된 데이터 또는 측정값으로 본다. 그러면 사전 확률 \( P\{B_i\} \)는 어떤 가설이나 모델에 대해서 미리 가지고 있던 사전 믿음(belief)으로 해석할 수 있다. 빈도 확률 \( P\{A|B_i \} \)는 해당 가설 또는 모델을 가진 상황에서 주어진 데이터가 얼마나 자주 관찰될 지에 대한 확률을 의미한다. 사후 확률 \( P\{B_i |A\} \)는 사전 가설 또는 모델에 대한 믿음의 정도를 관련 데이터를 이용하여 수정한 것으로 개선된 믿음으로 해석할 수 있다.
예를 들어보자.
사건 \( B \)를 어떤 사람이 암에 걸렸다는 가설로 보자. 그리고 사건 \( A \)를 암 진단 장비로 검사했을 때 결과가 암으로 나온다는 데이터로 본다. 그러면 \( P\{B\} \)는 그 사람이 암에 걸렸을지도 모른다고 믿는 사전 확률이다. 보통 암 환자가 인구의 \( 1 \% \)라고 한다면 그 사람도 그 정도의 확률로 암에 걸렸을 지도 모른다고 의심할 수 있다. 그래서 \( P\{B\}=0.01 \)로 놓는다. 암 진단 장비는 완벽하지 않으므로, 암 환자가 암 진단 장비로 검사했을 때 암으로 정확하게 판정할 확률을 \( 90\% \)라고 보고, 보통 사람을 암 환자로 오판할 확률을 \( 5\% \)라고 본다면 빈도 확률은 \( P\{A│B\}=0.9 \)이다. \( B^c \)를 사건 \(B \)의 여사건(complement event)으로서 그 사람이 암에 걸리지 않았다는 가설이라고 하면 \( P\{A│B^c \}=0.05 \)이다. 암에 걸렸다는 사건과 암에 걸리는 않았다는 사건은 서로 배타적이고 전체 표본 공간을 망라하는 사건이다. 그러면 암 환자 또는 일반 사람 가리지 않고 암 진단 장비가 암으로 판정하는 확률 \( P\{A\} \)는 전확률 정리에 의해서 다음과 같이 계산된다.
\[ \begin{align} P\{A\} &= P\{A│B\} P\{B\} + P \{A│B^c \} P\{B^c \} \\ \\ &= 0.9 (0.01)+0.05(0.99) \\ \\ &= 0.0585 \end{align} \]
이제 베이즈 정리에 의하면 어떤 사람이 암 진단 장비로 검사해서 암으로 판정을 받았을 경우, 그 사람이 암일 확률 즉 사후 확률 \( P\{B│A\} \)는 다음과 같이 계산된다.
\[ P\{B|A\}= \frac{P\{A|B\} P\{B\}}{ P\{A\}} = \frac{ 0.9 (0.01)}{0.0585 }=0.1538 \]
즉, \( 15.4\% \)정도가 나온다.
참고로 베이즈 정리를 만든 토마스 베이즈(Thomas Bayes)는 영국인으로서 목사였다고 한다.
'AI 수학 > 랜덤프로세스' 카테고리의 다른 글
| 랜덤변수의 함수와 샘플링 - 1 (0) | 2020.12.22 |
|---|---|
| 반복적인 기댓값 계산 (0) | 2020.12.12 |
| 샘플평균과 샘플분산 (0) | 2020.11.12 |
| IID 샘플 (0) | 2020.11.04 |
| 조건부 확률 (0) | 2020.10.27 |




댓글