DQN은 이산공간 상태변수에서만 작동하던 Q-러닝 알고리즘을 연속공간 상태변수로 확장시킨 것이었다.
일단 단순하게 Q-러닝을 바탕으로 만든 DQN 알고리즘은 다음과 같았다.
[1] DQN의 파라미터를 초기화한다. 그리고 [2]-[4]를 반복한다.
[2] 행동 \(\mathbf{a}_i\) 를 실행하여 천이샘플(transition sample) \(\{\mathbf{x}_i, \mathbf{a}_i, r_i, \mathbf{x}_{i+1}\}\) 를 모은다.
[3] \(y_i= r(\mathbf{x}_i, \mathbf{a}_i )+ \gamma \max_{\mathbf{a}^\prime} Q_\phi (\mathbf{x}_{i+1}, \mathbf{a}^\prime )\) 를 계산한다.
[4] \(\phi \gets \phi + \alpha_\phi \sum_i \left( y_i- Q_\phi (\mathbf{x}_i, \mathbf{a}_i ) \right) \nabla_\phi Q_\phi (\mathbf{x}_i, \mathbf{a}_i ) \) 로 신경망을 업데이트 한다.
이제 이 DQN 알고리즘의 문제점을 살펴보고 이를 극복할 수 있는 방안에 대해서 알아본다.
알고리즘의 [2]번은 천이샘플을 모아서 바로 행동가치 신경망의 파라미터를 업데이트하는 것이다. 여기에는 강화학습 고유의 문제가 숨어 있다. 바로 궤적 데이터가 시간적으로 상관되어 있다는 것이다.
강화학습에서 신경망의 파라미터를 업데이트할 때 사용하는 최적화 방법은 확률경사하강법(SGD)이다. 확률경사하강법은 각 샘플이 서로 독립적이고 균등하게 분포되어 있다는 가정하에서 성립한다. 하지만 일반적인 지도학습에서 사용하는 데이터와는 달리 강화학습의 데이터는 에이전트가 환경과 상호작용하면서 순차적으로 얻는 것이기 때문에 데이터가 시간적으로 서로 상관되어 있다. 따라서 이러한 상관관계를 깨는 것이 필요하다.
온-폴리시(on-policy) 방법에서는 이러한 상관관계를 줄이기 위해서 멀티 에이전트를 병렬적으로 운용하는 방법을 사용하기도 하는데, 오프-폴리시(off-policy) 방법에서는 이보다 상대적으로 손쉬운 방법을 사용할 수 있다. 오프-폴리시 방법은 다른 정책으로 생성한 데이터로 현재의 정책을 업데이트 할 수 있기 때문이다.
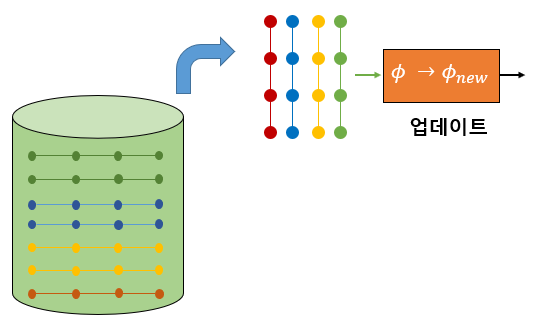
DQN에서는 천이샘플(또는 학습 데이터)를 바로 학습에 사용하지 않고 일단 리플레이 버퍼(replay buffer)라는 곳에 저장해 둔다.

그리고 어느 정도 이상의 데이터가 모이면 버퍼에서 데이터를 무작위로 꺼내서 학습에 이용한다. 무작위로 데이터를 추출하기 때문에 순차적으로 구성된 데이터에 비해 상관관계를 크게 줄일 수 있다.
두번째는 탐색(exploration)의 문제다. Q-러닝은 확정적 정책이므로 불확실한 환경을 적극적으로 탐색할 수 있는 무작위성(randomness)이 없다. Q-러닝과 DQN에서는 이러한 문제를 해결하고자 \(\epsilon - \)탐욕(greedy) 탐색 방법을 사용한다. \(\epsilon -\)탐욕 탐색 방법은 \(1-\epsilon\) 확률로 탐욕 정책을 실행하고 나머지 확률로 무작위 행동을 선택하는 것이다.
\[ \pi (\mathbf{a}_t | \mathbf{x}_t )= \begin{cases} 1-\epsilon, & \mbox{if } \mathbf{a}_t = \arg \max_{\mathbf{a}_t} Q_\phi (\mathbf{x}_t, \mathbf{a}_t) \\ \epsilon, & \mbox{else random} \end{cases} \]
일반적으로 학습 초기에는 \(\epsilon\) 값을 크게 하여 탐색 비중을 높이고 학습을 진행하면서 \(\epsilon\) 값을 줄여 탐색 대신 활용(exploitation)의 비중을 높이는 방법을 사용한다.
세번째는 학습의 수렴성 문제다. Q-러닝에서는 벨만 백업이 축소(contraction) 연산자이기 때문에 최적 행동가치 함수로 수렴했다. 하지만 DQN에서는 벨만 백업과 행동가치 함수 추정을 번갈아 가면서 사용하기 때문에 연산자의 축소 여부를 따져봐야 한다.
\[ \begin{align} & y_i = r(\mathbf{x}_i, \mathbf{a}_i )+ \gamma \max_{\mathbf{a}^\prime} Q_\phi (\mathbf{x}_{i+1}, \mathbf{a}^\prime ) \\ \\ & \phi \gets \arg \min_\phi \sum_i \frac{1}{2} \lVert y_i- Q_\phi (\mathbf{x}_i, \mathbf{a}_i) \rVert^2 \end{align} \]
벨만 백업은 \(\infty -\)놈(norm) 축소 연산자이고 행동가치 함수 추정은 \(2-\)놈 축소 연산자이긴 하지만 두 개를 결합하는 이터레이션은 축소 연산자가 아니기 때문에, 안타깝게도 행동가치 함수가 어떤 한 포인트로 수렴한다는 보장이 없다. 하지만 다행스럽게도 실제 적용에 있어서는 대부분의 경우 잘 수렴하는 편이다.
네번째는 학습의 안정성 문제다. DQN에서도 A2C 알고리즘과 마찬가지로 부트스트래핑 방법을 사용했다. 시간차 타깃이 신경망을 업데이트 할 때 마다 계속 달라지므로 학습이 불안정해질 수 있다. 더구나 DQN은 함수 추정(또는 함수 근사화), 부트스트래핑, 오프-폴리시 학습 방법 등 죽음의 삼인조(Deadly Triad)에 해당하므로 특히 안정성에 문제가 있다.
다섯번째는 신경망 학습에 사용된 경사하강법(gradient descent) 문제다. 알고리즘의 [4]번은 경사하강법이 아니다. 왜냐하면 시간차 타깃 \(y_i\)도 \(\phi\) 의 함수이기 때문이다.
\[ \begin{align} \phi & \gets \phi + \alpha_\phi \sum_i \left( y_i-Q_\phi (\mathbf{x}_i, \mathbf{a}_i ) \right) \nabla_\phi Q_\phi (\mathbf{x}_i, \mathbf{a}_i ) \\ \\ &= \phi + \alpha_\phi \sum_i \left(r(\mathbf{x}_i, \mathbf{a}_i )+ \gamma \max_{\mathbf{a}^\prime} Q_\phi (\mathbf{x}_{i+1}, \mathbf{a}^\prime ) -Q_\phi (\mathbf{x}_i, \mathbf{a}_i ) \right) \nabla_\phi Q_\phi (\mathbf{x}_i, \mathbf{a}_i ) \end{align} \]
원래대로 하면 손실함수의 그래디언트를 계산할 때 시간차 타깃 \(y_i\) 도 미분해야 맞다.
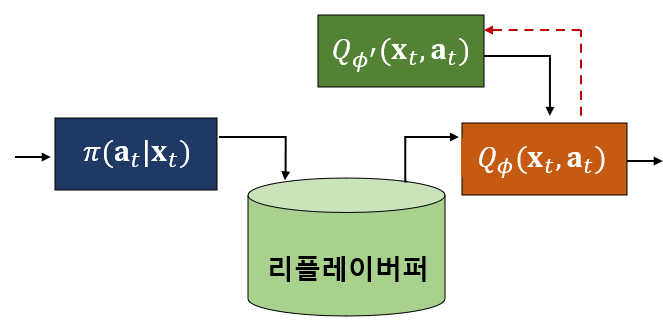
네번째와 다섯번째의 문제점을 해결하기 위하여 DQN에서는 Q 신경망과는 별도로 타깃(target) 신경망을 도입하였다. 타깃 신경망은 시간차 타깃 \(y_i\) 를 계산하기 위한 것으로 Q 신경망을 업데이트하는 동안 타깃 계산에 사용되는 파라미터를 고정시킨다. 그리고 일정 시간마다 Q 신경망의 파라미터로 주기적으로 업데이트 시킨다.

타깃 신경망의 파라미터를 \(\phi^\prime\) 이라고 하면 시간차 타깃 \(y_i\) 는 다음과 같이 된다.
\[ y_i = r(\mathbf{x}_i, \mathbf{a}_i )+ \gamma \max_{\mathbf{a}^\prime} Q_{\phi^\prime} (\mathbf{x}_{i+1}, \mathbf{a}^\prime ) \]
이제 \(y_i\) 는 \(\phi\) 의 함수가 아니기 때문에 알고리즘의 [4]번은 경사하강법이 된다.
DQN에서는 일정시간 마다 주기적으로 타깃 신경망의 파라미터를 Q 신경망의 파라미터로 업데이트하는 방법을 사용하지만, 다음 식과 같이 타깃 신경망의 파라미터가 Q 신경망의 파라미터를 느린 속도로 따라가는 방법도 많이 사용되고 있다.
\[ \phi^\prime \gets \tau \phi + (1- \tau) \phi^\prime \]
여기서 \(\tau\) 는 아주 작은 값으로 설정한다.
DQN 알고리즘을 최종 정리하면 다음과 같다.
[1] Q 신경망의 파라미터를 초기화한다.
[2] Q 신경망의 파라미터를 타깃 신경망에 복사한다.
[3] 리플레이 버퍼를 초기화 한다. 그리고 [4]-[8]을 반복한다.
[4] \(\epsilon -\)탐욕 정책을 실행하여 발생된 천이샘플(transition sample) \(\{\mathbf{x}_i, \mathbf{a}_i, r_i, \mathbf{x}_{i+1}\}\) 를 리플레이 버퍼에 저장한다.
[5] 리플레이 버퍼에서 \(N\) 개의 천이샘플 \(\{\mathbf{x}_i, \mathbf{a}_i, r_i, \mathbf{x}_{i+1}\}\) 를 무작위로 추출한다.
[6] \( y_i = r(\mathbf{x}_i, \mathbf{a}_i )+ \gamma \max_{\mathbf{a}^\prime} Q_{\phi^\prime} (\mathbf{x}_{i+1}, \mathbf{a}^\prime ) \) 를 계산한다.
[7] \( \phi \gets \phi + \alpha_\phi \sum_i \left( y_i-Q_\phi (\mathbf{x}_i, \mathbf{a}_i ) \right) \nabla_\phi Q_\phi (\mathbf{x}_i, \mathbf{a}_i ) \)로 Q 신경망을 업데이트 한다.
[8] \( \phi^\prime \gets \tau \phi + (1- \tau) \phi^\prime \) 로 타깃 신경망을 업데이트 한다.
'AI 딥러닝 > RL' 카테고리의 다른 글
| Double DQN 알고리즘 (0) | 2021.05.11 |
|---|---|
| Tensorflow2로 만든 DQN 코드: CartPole-v1 (0) | 2021.05.04 |
| DQN 알고리즘 - 1 (0) | 2021.05.02 |
| 가치 이터레이션에서 Q-러닝으로 (0) | 2021.05.01 |
| 가치 이터레이션 (Value Iteration) (0) | 2021.04.29 |




댓글