LTI는 Linear Time-Invariant의 약자다. 선형이고 시불변이라는 뜻이다. 따라서 "LTI 시스템"은 선형 시불변 시스템의 줄인 말이다. 컨볼루션을 얘기하다가 왜 갑자기 LTI 시스템이냐 라고 생각할 지도 모르겠다. LTI 시스템에서 컨볼루션 정의가 나오기 때문이다. LTI 시스템 뿐 만 아니라 확률론 등에서도 나오지만, CNN의 컨볼루션은 LTI 시스템에 나오는 컨볼루션이다.
그럼 선형 시스템이 무엇인지, 시불변 시스템이 무엇인지 알아보자.
먼저, 시스템이란 어떤 입력에 대해서 반응하여 동작하는 장치나 구성품의 집합을 뜻한다. 시스템의 반응을 출력 또는 응답이라고 한다. 시스템은 꼭 물리적인 장치나 구성품 또는 하드웨어일 필요는 없고, 알고리즘 또는 소프트웨어일 수도 있다. 아니면 사회경제 제도일 수도 있다. 세상에는 무인기 시스템, 제어 시스템, 금융 시스템 등등 많은 시스템이 있다. 신호처리 분야에서는 시스템을 필터(filter) 또는 커널(kernel)라고 한다.
수학적으로는 시스템을 입력에서 출력을 연결하는 연산자(operator)로 표현할 수 있다.
\[ y[n] = \mathbb{F}(x[n]) \]
여기서는 이산시간(discrete-time) 신호와 시스템만을 다룬다. 그러면 \( n \)은 인덱스로서 정수 값을 갖는다. 이 인덱스는 보통 시간스텝(time step)을 나타내지만 이미지 처리에서는 공간상의 위치를 나타내는 배열 또는 순서를 뜻하기도 한다. \( x[n] \)은 정수 인덱스 \( n \)을 변수로 하는 함수로서 입력 또는 입력신호라고 한다. \( y[n] \)은 정수 인덱스 \( n \)을 변수로 하는 함수로서 출력 또는 출력신호라고 한다. \( \mathbb{F} \)는 시스템 또는 연산자로서 입력 \( x[n] \)과 출력 \( y[n] \)사이의 관계식을 나타낸다.
예를 들면 다음과 같은 수식이 시스템을 표현한 것이다.
\[ \begin{align} y[n] &= x[n]-x[n-1] \\ \\ y[n] &= (x[n])^2 \end{align} \]
시스템은 여러가지 기준으로 다양하게 분류될 수 있는데, 우선 시스템을 선형 시스템과 비선형 시스템으로 분류해 보자. 선형 시스템은 다음 두 가지로 판별한다. 우선 입력의 크기를 \( \alpha \)배 키웠을 때 출력도 \( \alpha \)배가 커지는 지, 두 번째는 두 개의 서로 다른 입력 \( x_1 [n] \)과 \( x_2 [n] \)를 더해서 시스템에 인가했을 때 출력도 각각의 입력에 해당하는 출력이 더해져서 나오는지 확인하는 것이다. 만약 이 두 가지가 모두 충족되면 그 시스템은 중첩의 원리를 만족한다고 하며 선형 시스템이라고 부른다. 수식으로 한꺼번에 표현하면 다음과 같다.
\( y_1[n] = \mathbb{F}(x_1[n]) \), \( y_2[n] = \mathbb{F}(x_2[n]) \) 일 때,
\[ \mathbb{F}(\alpha_1 x_1[n]+\alpha_2 x_2[n]) = \alpha_1 \mathbb{F} (x_1[n]) + \alpha_2 \mathbb{F} (x_2 [n]) \]
\( \qquad \qquad \qquad \qquad = \alpha_1 y_1[n]+\alpha_2 y_2[n] \) 이면,
\( \mathbb{F} \) 는 선형 시스템이다.
그럼 시스템 \( y[n] = x[n]-x[n-1] \)이 선형인지 알아보자. 정의대로 하면,
\( y_1[n] = x_1[n]-x_1[n-1] \), \( y_2[n] = x_2[n]-x_2[n-1] \) 일 때,
\[ (\alpha_1 x_1[n]+\alpha_2 x_2[n]) - (\alpha_1 x_1[n-1] +\alpha_2 x_2[n-1]) \]
\[ = \alpha_1 y_1[n] + \alpha_2 y_2[n] \]
이므로 선형 시스템이다.
이번에는 시스템 \( y[n] = (x[n])^2 \)이 선형인지 알아보자. 마찬가지로 정의대로 하면,
\( y_1[n] = (x_1[n])^2 \), \( y_2[n] = (x_2[n])^2 \) 일 때,
\[ (\alpha_1 x_1[n]+\alpha_2 x_2[n])^2 \neq \alpha_1 y_1[n] + \alpha_2 y_2[n] \]
이므로 선형 시스템이 아니다. 선형이 아니므로 비선형 시스템이다.
다음으로 시스템 \( y[n] = x[n]+b \)가 선형인지 알아보자. 여기서 \( b \)는 상수라고 한다. 역시 정의대로 하면,
\( y_1[n] = x_1[n]+b \), \( y_2[n] = x_2[n]+b \) 일 때,
\[ (\alpha_1 x_1[n]+\alpha_2 x_2[n])+b \neq \alpha_1 y_1[n] + \alpha_2 y_2[n] \]
이므로 선형 시스템이 아니다. 보기에는 선형 시스템 같은데 정의대로 하니까 아니다. y-절편이 있는 게 문제다. 이런 경우에는 그림과 같이 좌표축을 살짝 평행 이동해 주면 선형이 되므로 비선형 시스템이라고 하지 않고, 어파인(affine) 시스템이라고 한다. 어파인 시스템도 선형 시스템으로 간주한다.
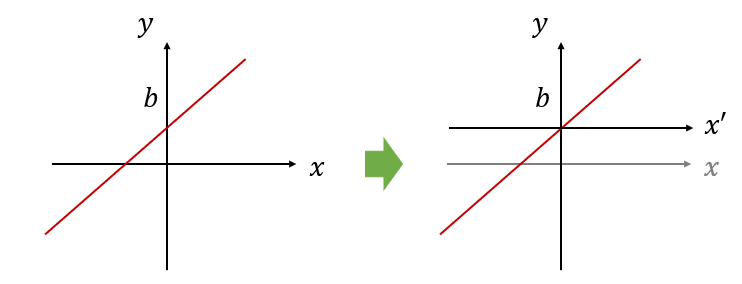
선형 시스템은 중첩의 원리를 만족하기 때문에 몇 가지 입력만으로도 시스템의 모든 동특성을 파악할 수 있다. 선형 시스템에서는 서울에 사는 나비의 작은 날개 짓으로 뉴욕의 폭풍을 만들 일은 없다. 입력의 작은 차이가 예기치 않은 큰 출력의 변화를 초래하지 않는다. 하지만 비선형 시스템에서는 이와 같은 일이 가능하다.
아직 컨볼루션이 안 나왔는데, 다음 포스트에서는 시불변 시스템을 먼저 살펴본 후에 LTI 시스템과 컨볼루션이 어떻게 연결되는지 알아보겠다.
'AI 딥러닝 > DLA' 카테고리의 다른 글
| [CNN] 컨볼루션 쉽게 계산하기 (0) | 2020.07.25 |
|---|---|
| [CNN] 컨볼루션 공식대로 계산하기 (0) | 2020.07.25 |
| [CNN] LTI 시스템과 컨볼루션 (0) | 2020.07.23 |
| [CNN] LTI 시스템 – 시불변 (0) | 2020.07.21 |
| [CNN] 컨볼루션(convolution)이란 (0) | 2020.07.20 |




댓글