적합직교분해(POD) 또는 주성분 분석(PCA)은 \(n\)차원 공간상에서 \(d\)개의 POD 모드(mode) \(\mathbf{w}_1, \mathbf{w}_2, ..., \mathbf{w}_d\)로 구성된 부분 공간에 데이터 벡터 \(\mathbf{y}(t)\)를 투사(projection)할 때 투사 오차가 최소가 되도록 POD 모드를 결정하는 알고리즘이다.
\[ \begin{align} \mathbf{y}^{(i)} & \approx \sum_{j=1}^d a_{ij} \mathbf{w}_j \\ \\ &= \begin{bmatrix} \mathbf{w}_1 & \mathbf{w}_2 & \cdots & \mathbf{w}_d \end{bmatrix} \begin{bmatrix} a_{i1} \\ a_{i2} \\ \vdots \\ a_{id} \end{bmatrix} \\ \\ &= W \mathbf{a}_i \end{align} \]
여기서 \(a_{ij}\)는 모드 계수(modal coefficients)다. POD에서는 데이터와 모드 계수에 시간 개념을 도입하여 \(\mathbf{y}^{(i)}=\mathbf{y}(t_i ), a_{ij}= a_j (t_i ), \mathbf{a}_i= \mathbf{a}(t_i)\) 로 쓴다.
데이터 벡터 \(\mathbf{y}^{(i)}\)를 센서로 측정한 어떤 값(예를 들면 얼굴 사진) 또는 어떤 미분 방정식을 만족하는 해(예를 들면 싯점 \(t=t_i\)에서 공기 속도 벡터 필드, 압력 필드 등)로 본다면, 어떤 경우에는 \(\mathbf{y}^{(i)}\)를 구성하는 일부 데이터에 손상이 있거나 탈락(missing)되어 있는 등 데이터 결함이 있을 수 있다.
예를 들면 얼굴 사진의 일부가 음영처리 됐다거나, 제한된 수량의 센서로 인해서 유동장의 일부 위치에서만 유동의 속도를 측정했다든가 하는 경우다. 이처럼 일부 탈락되어 있는 데이터셋을 개피(gappy) 데이터셋이라고 한다.

Gappy POD는 POD 모드가 주어졌을 때, 개피 데이터셋으로부터 완전한 데이터셋을 재구성할 수 있는 알고리즘이다. Gappy POD는 일부분이 가려져 있는 얼굴 사진에서 완전한 이미지를 재구성하거나, 제한된 수의 압력 센서를 이용하여 에어포일(airfoil) 주위의 압력장을 재구성하는 데 적용되어 성공을 거둔 바 있다. 더 나아가서 일부 탈락된 데이터셋으로 반복적인 방법을 사용하여 POD 모드 자체까지 복원할 수 있는 Gappy POD 방법도 개발되어 있다.
개피 데이터를 다음과 같이 표시하기로 하자.
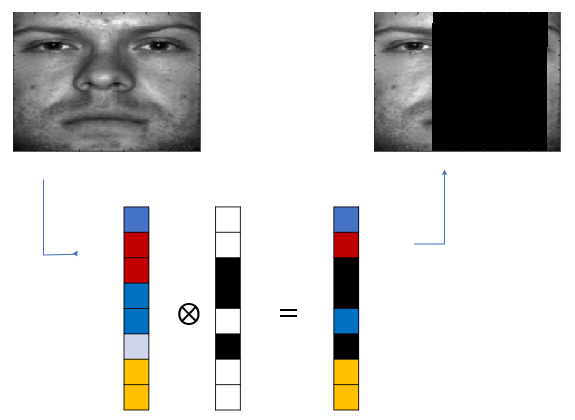
\[ \tilde{\mathbf{y}}^{(i)} = \mathbf{m}_i \otimes \mathbf{y}^{(i)} \]
여기서 벡터 \(\mathbf{m}_i\)을 마스크 벡터(mask vector)라고 하며 데이터의 특정 성분이 탈락되어 있으면 \(0\), 완전하면 \(1\)의 값을 갖는다. \(\otimes\)는 두 벡터의 성분 별 곱셈을 나타낸다.
모드 계수 \(\mathbf{a}_i\)는 데이터셋 \(\mathbf{y}^{(i)}\)의 성분을 모두 알아야 계산할 수 있는데, 이처럼 데이터가 탈락되어 있으면 계산할 수 없다. 그러면 \(\mathbf{a}_i\)를 어떻게 계산해야 할까.
이상적인 상황과 구별하기 위하여 개피 데이터셋에 대한 모드 계수를 \(\tilde{\mathbf{a}}_i\)로 표기한다. 그러면 개피 데이터은 근사적으로 다음과 같이 표현할 수 있다. 여기서 POD 모드 \(\mathbf{w}_j\)는 미리 주어졌다고 가정한다.
\[ \begin{align} \tilde{\mathbf{y}}^{(i)} & \approx \mathbf{m}_i \otimes \sum_{j=1}^d \tilde{a}_{ij} \mathbf{w}_j \\ \\ &= \mathbf{m}_i \otimes \left( W \tilde{\mathbf{a}}_i \right) \end{align} \]
위 식에서 \( \sum_{j=1}^d \tilde{a}_{ij} \mathbf{w}_j \)는 원래 데이터를 복원시킨 것에 해당하므로, \( \tilde{\mathbf{a}}_i \)는 탈락된 데이터를 제외한 나머지 데이터로 \( \tilde{\mathbf{y}}^{(i)} \)와 \( \sum_{j=1}^d \tilde{a}_{ij} \mathbf{w}_j \)의 차이를 최소화하도록 추정하는 것이 타당할 것이다.
\[ \begin{align} \arg\min_{\tilde{\mathbf{a}}_i} J &= \lVert \tilde{\mathbf{y}}^{(i)} - \sum_{j=1}^d \tilde{a}_{ij} \tilde{\mathbf{w}}_j^i \rVert_2^2 \\ \\ &= \lVert \tilde{\mathbf{y}}^{(i)}- \tilde{W}^i \tilde{\mathbf{a}}_i \rVert_2^2 \end{align} \]
여기서 \( \tilde{\mathbf{w}}_j^i = \mathbf{m}_i \otimes \mathbf{w}_j \) 는 POD 모드를 마스킹한 벡터이다. 최소값을 구하기 위해서 \(J\)를 \(\tilde{\mathbf{a}}_i\)로 미분하여 \(0\)으로 놓으면 다음 식을 얻을 수 있다.
\[ ( \tilde{W}^i )^T \tilde{W}^i \tilde{\mathbf{a}}_i= ( \tilde{W}^i )^T \tilde{\mathbf{y}}^{(i)} \]
마스크 된 POD 모드 \( \tilde{\mathbf{w}}_j^i \)는 더 이상 직교 벡터가 아니다. 하지만 만약 탈락된 데이터가 없다면 \( \mathbf{m}_i= [1 \ \cdots \ 1]^T\)이므로 \(\tilde{W}^i =W\)가 되는데, POD 모드는 서로 직각이기 때문에 \((\tilde{W}^i )^T \tilde{W}^i=I\) 가 된다. 따라서 \(\tilde{\mathbf{a}}_i=\mathbf{a}_i\)가 된다. 개피 데이터라 할 지라도 탈락된 데이터가 아주 적다면 \((\tilde{W}^i )^T \tilde{W}^i \approx I \)가 될 것이다.
\( (\tilde{W}^i )^T \tilde{W}^i \) 은 준정정(semi-positive) 행렬이기 때문에 \(0\) 이상의 값을 갖는 실수 고유값과 서로 직각인 실수 고유벡터를 갖는다. \( ( \tilde{W}^i )^T \tilde{W}^i \) 를 고유값 분해(Eigen Decomposition)하면 다음과 같다.
\[ ( \tilde{W}^i )^T \tilde{W}^i = P \Lambda P^T \]
여기서 \(P= [ \mathbf{v}_1 \ \cdots \ \mathbf{v}_d] \)는 고유벡터 행렬, \(\Lambda =diag ( \lambda_1, ..., \lambda_d)\) 는 고유값 대각 행렬이다.
이를 이용하여 위 식에서 \(\tilde{\mathbf{a}}_i\)를 계산하면 다음과 같다.
\[ \begin{align} \tilde{\mathbf{a}}_i &= P \Lambda^{-1} P^T (\tilde{W}^i )^T \tilde{\mathbf{y}}^{(i) } \\ \\ &= \sum_{j=1}^d \frac{ \mathbf{v}_j^T \left( (W ̃^i )^T \tilde{\mathbf{y}}^{(i)} \right) }{ \lambda_j } \mathbf{v}_j \end{align} \]
또는, 역행렬을 이용하여 계산할 수도 있다.
\[ \tilde{\mathbf{a}}_i = \left( (\tilde{W}^i )^T \tilde{W}^i \right)^{-1} (\tilde{W}^i )^T \tilde{\mathbf{y}}^{(i) } \]
원래 데이터 \(\mathbf{y}^{(i)}\)는 다음 식으로 복원시킬 수 있다.
\[ \begin{align} \hat{\mathbf{y}}^{(i)} &= \sum_{j=1}^m \tilde{a}_{ij} \mathbf{w}_j \\ \\ &= W \tilde{\mathbf{a}}_i \end{align} \]
'유도항법제어 > 데이터기반제어' 카테고리의 다른 글
| [DMD-1] 동적모드분해 (Dynamic Mode Decomposition) (0) | 2022.10.26 |
|---|---|
| [POD-4] Gappy POD 매트랩 예제 (0) | 2021.03.01 |
| [POD-2] 스냅샷 적합직교분해 (snapshot POD) (0) | 2021.03.01 |
| [POD-1] 고전 적합직교분해 (classical POD) (0) | 2021.02.28 |
| [PCA–4] PCA 예제: Eigenfaces (0) | 2021.02.24 |




댓글