전통적으로 비행제어 법칙은 게인 스케줄링(gain scheduling) 기법을 이용하여 설계되었다.
게인 스케줄링은 선형제어 설계 방법을 비선형 시스템에 적용하기 위한 것으로서 제어 게인(gain)을 작동 조건에 따라 다르게 설계하는 기법이다. 게인 스케줄링에서는 다양한 비행조건에서 선형화된 여러 개의 운동 모델에 기반하여 제어 게인을 설계한 후 비행조건에 따라서 제어 게인을 변화시킨다. 이를 이용하면 선형제어 시스템의 작동 영역을 일부로 한정시키지 않고 비행영역(flight envelope) 전체로 확장시킬 수 있다.
게인 스케줄링을 이용한 제어 시스템은 일반적인 제어 시스템과 달리 제어 게인이 비행 조건에 따라 변하기 때문에 설계하는데 시간이 많이 걸리고 반복하는데 비용이 많이 들며 공학적 경험에 크게 의존한다. 또한 최근 고성능 전투기가 높은 기동성과 함께 고도의 비선형 비행 체제로 확장되었기 때문에 게인 스케줄링을 이용한 비행제어 법칙 설계는 매우 복잡해질 수 있다.
최근에는 이러한 항공기 운동의 비선형성을 설계 과정에서 직접 다룰 수 있는 동적 역변환 (DI, dynamic inversion) 제어가 사용되고 있다. 이미 F/A-18 Hornet 전투기에서 성공적으로 작동하는 것을 시연하였고 현재 F-35를 비롯하여 다양한 군용기 및 헬리콥터에 널리 사용되는 비행 제어 설계 방법으로 발전했다.

DI(동적 역변환) 제어는 항공기 운동의 비선형성을 직접 다룰 수 있기 때문에 단일 제어 법칙 구조로 전체 비행영역에서 작동할 수 있으며 복잡한 게인 스케줄링을 필요로 하지 않는다. 또한 이론적으로 매우 간단하며 일반적인 제어 법칙 구조로 인해 항공기 모델이 변경되어도 제어 법칙을 쉽게 업데이트할 수 있고 서로 다른 항공기에 제어 법칙을 재사용하는 데에도 적합하다.
DI(동적 역변환) 제어의 핵심 아이디어는 원래의 항공기 동역학을 '제거'하고 원하는 항공기 응답을 '도입'하는 데에 있다. DI(동적 역변환)는 본래 비선형 시스템에 적용됐을 때 위력을 발휘하지만 어떻게 작동하는지 원리를 쉽게 이해할 수 있도록 일단 선형 시스템에 먼저 적용해 보도록 한다.
다음과 같은 선형 시스템이 있다.
\[ \begin{align} \dot{\mathbf{x}} &= A \mathbf{x}+B \mathbf{u} \tag{1} \\ \\ \mathbf{y} &= C \mathbf{x} \end{align} \]
여기서 \(\mathbf{x}(t) \in \mathbb{R}^n\) 는 상태변수, \(\mathbf{u}(t) \in \mathbb{R}^p\) 는 제어입력이다. \(\mathbf{y}(t) \in \mathbb{R}^p\) 는 출력으로서 센서로 측정되는 값이 아니라 어떤 제어 목적을 표현하는 제어변수(controlled variable)이다.
DI(동적 역변환)에서는 시스템의 입력과 출력의 갯수가 같은 '정방형' 시스템을 가정한다. 보통 1개의 자유도에 1개의 제어입력이 필요하므로 위와 같은 정방형 시스템 가정이 유효한 경우가 많지만, 최근에는 자유도 보다도 훨씬 많은 제어입력 수단을 장착한 고성능 항공기가 많이 있다. 이때는 여러가지 제어력 재할당 기법을 사용하여 제어입력의 수를 줄여서 정방형 시스템으로 만들어야 한다.
시스템 (1)의 제어 목표는 출력 \(\mathbf{y}(t)\) 가 기준 응답 \(\mathbf{r}(t)\) 를 추종하도록 제어입력 \(\mathbf{u}(t)\) 를 결정하는 것이다. 즉 다음과 같이 정의되는 추종오차 \(\mathbf{e}(t)\) 를 \(0\) 으로 만드는 것이 제어 목표이다.
\[ \mathbf{e}(t)=\mathbf{r}(t)-\mathbf{y}(t) \tag{2} \]
여기서 기준 응답은 원하는 항공기 응답을 의미한다. DI(동적 역변환)에서는 수식상에 제어입력 \(\mathbf{u}(t)\) 가 명시적으로 나타날 때까지 출력 \(\mathbf{y}(t)\) 를 미분한다. 식 (1)에 미분을 취하면,
\[ \dot{\mathbf{y}}=C \dot{\mathbf{x}}=CA\mathbf{x}+CB\mathbf{u} \tag{3} \]
이 되는데 만약 \(CB \ne 0\) 이라면 수식상에서 \(\mathbf{u}(t)\) 가 명시적으로 나타난 것이다. 만약 \(CB=0\) 이면 위 식을 한번 더 미분한다.
\[ \ddot{\mathbf{y}} =CA \dot{\mathbf{x}} +CB \dot{\mathbf{u}}=CA^2 \mathbf{x}+CAB\mathbf{u} \tag{4} \]
만약 \(CAB \ne 0\) 이라면 수식상에서 \(\mathbf{u}(t)\) 가 나타난 것이고, \(CAB=0\) 이면 \(\mathbf{u}(t)\) 가 명시적으로 나타날 때까지 위 식을 계속 미분해야 한다. 일단 \(CB \ne 0\) 이라고 가정한다. 그리고 다음과 같이 보조입력(auxiliary input) \(\nu\) 를 정의한다.
\[ \nu =CA \mathbf{x}+CB \mathbf{u} \tag{5} \]
그러면 제어입력은 다음과 같이 계산되고,
\[ \mathbf{u}=(CB)^{-1} ( \nu -CA\mathbf{x} ) \tag{6} \]
이 식을 식 (3)에 대입하면 다음과 같이 된다.
\[ \begin{align} \dot{\mathbf{y}} &=CA \mathbf{x}+CB(CB)^{-1} (\nu -CA\mathbf{x}) \tag{7} \\ \\ &= \nu \end{align} \]
따라서 식 (6)과 같은 방식으로 제어입력을 정의하면 항공기 동역학이 '제거'되고 단순한 적분기로 바뀐다.
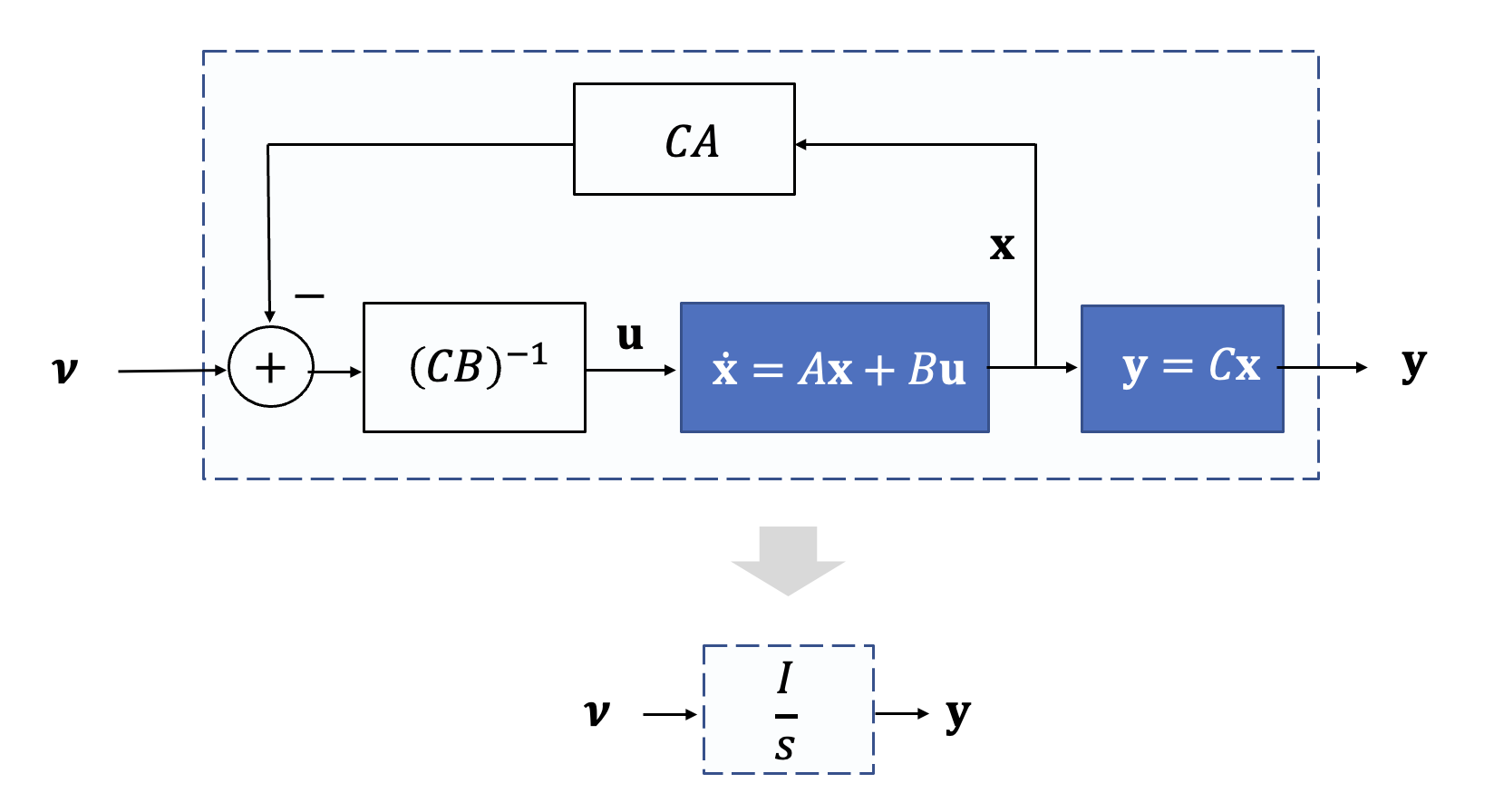
식 (2)에 의하면 식 (7)은
\[ \dot{\mathbf{e}} = \dot{\mathbf{r}} - \nu \tag{8} \]
이 된다. 위 식을 오차 동역학(error dynamics)이라고 한다. 오차의 차원이 \(p\) 이므로 식 (8)에 의하면 오차 동역학은 원점에 극점(pole)이 \(p\) 개 있다.
보조입력 \(\nu\) 는 오차 동역학이 안정하고 비행성 요구조건과 같은 특정 요구조건을 충족하도록 정한다. 다양한 선형 제어법칙을 사용할 수 있는데 예를 들면 강인제어(robust control)나 LQG/LTR등을 들 수 있다. 그 중에서 가장 간단한 형태는 다음과 같다.
\[ \nu =\dot{\mathbf{r}} + K \mathbf{e} \tag{9} \]
그러면 오차 동역학은 다음과 같이 된다.
\[ \dot{\mathbf{e}} + K \mathbf{e}=0 \tag{10} \]
\(K\) 가 정정행렬(positive-definite matrix)이면 오차 동역학은 안정하다. 식 (9)를 (6)에 대입하면 제어입력은 다음과 같이 된다.
\[ \mathbf{u}=(CB)^{-1} (\dot{\mathbf{r}}+K\mathbf{e}-CA\mathbf{x}) \tag{11} \]
다음 그림은 DI(동적 역변환) 제어 구조를 보여준다. 식 (9)는 외부 루프를 구성하고 식 (6)은 상태변수 피드백 제어로서 내부 루프를 구성한다. 내부 루프를 피드백 선형화(feedback linearization) 루프라고도 한다 (선형 시스템에 대해서 DI를 설계했으므로 선형화라는 말이 아직 실감이 안날 것이다). 내부 루프의 기능은 \(\nu\) 부터 \(\mathbf{y}\) 까지의 신호 흐름이 원점에 극점이 \(p\) 개 있는 적분기와 같게 만드는 것이다. \(\dot{\mathbf{r}}\) 은 속도 피드포워드(feedforward) 항이다.

DI(동적 역변환) 제어 법칙 (11)에 의하면 \(CA\) 와 \(CB\) 가 필요하므로 시스템의 동역학 모델을 제어기에 내장해야 함을 의미한다. 또한 내부 루프는 \(\mathbf{x}\) 가 필요하므로 전 상태변수 피드백(full state feedback) 제어에 해당한다.
언뜻 보기에 오차가 \(0\) 으로 수렴하므로 성공적으로 제어 법칙 설계가 끝난 것 같지만 아직 따져봐야 할 것이 있다. 바로 제어 시스템의 내부 안정성에 관한 문제다. 또 하나는 식 (3)에서 \(CB=0\) 으로 나와서 \(\mathbf{u}(t)\) 가 명시적으로 나타날 때까지 수식을 여러 차례 미분해야만 하는 경우이다.
'유도항법제어 > 비행제어' 카테고리의 다른 글
| [PX4] 멀티콥터 자세제어 알고리즘 - 1 (0) | 2023.02.22 |
|---|---|
| [DI-2] 내부 동역학 (Internal Dynamics) (0) | 2023.01.20 |
| 비선형 시스템과 매니폴드 (Manifold) (0) | 2023.01.01 |
| 선형 시스템과 부분공간 (Subspace) (0) | 2022.12.27 |
| 행렬지수함수 (Matrix Exponential) 계산 (0) | 2022.12.24 |




댓글