J2 섭동에 의한 궤도요소의 시간 변화율 - 2

J2 섭동에 의한 궤도요소의 시간 변화율을 다음과 같이 유도한 바 있다 (https://pasus.tistory.com/350).

 

\[ \begin{align} \frac{da}{dt} & = 3J_2 \frac{a^2 \mu R_e^2 }{hr^4} \begin{bmatrix} e \sin \theta \ (3 \sin^2 i \sin^2 (\omega + \theta)-1) \\ -(1+e \cos \theta ) \sin^2 i \sin 2(\omega+ \theta) \end{bmatrix} \tag{1} \\ \\ \frac{de}{dt} &= \frac{3}{2} J_2 \frac{\mu R_e^2}{hr^3 } \begin{bmatrix} \frac{h^2}{\mu r} \sin \theta \ (3 \sin^2 i \sin^2 (\omega + \theta)-1) \\ -[ (2+e \cos \theta ) \cos \theta+e ] \sin^2 i \sin 2(\omega +\theta) \end{bmatrix} \\ \\ \frac{di}{dt} &= \frac{3}{2} J_2 \frac{\mu R_e^2}{ehr^3} \begin{bmatrix} \frac{h^2}{\mu r} \cos \theta \ (1-3 \sin^2 i \sin^2 (\omega+\theta) ) \\ -(2+e \cos \theta ) \ \sin \theta \sin^2 i \sin 2(\omega+\theta) \\ +2e \cos^2 i \sin^2 (\omega+ \theta) \end{bmatrix} \\ \\ \frac{d\Omega}{dt} &= -3 J_2 \frac{\mu R_e^2}{hr^3 } \cos i \sin^2 (\omega+\theta) \\ \\ \frac{d\omega }{dt} &= \frac{3}{2} J_2 \frac{\mu R_e^2}{ehr^3 } \begin{bmatrix} \frac{h^2}{\mu r} \cos \theta \ (1-3 \sin^2 i \sin^2 (\omega +\theta) ) \\ -(2+e \cos \theta ) \sin \theta \sin^2 i \sin 2(\omega +\theta) \\ +2e \cos^2 i \sin^2 (\omega+\theta) \end{bmatrix} \\ \\ \frac{d \theta}{dt} &= \frac{h}{r^2 }+ \frac{3}{2} J_2 \frac{\mu R_e^2}{ehr^3} \begin{bmatrix} \frac{h^2}{\mu r} \cos \theta \ (3 \sin^2 i \sin^2 (\omega + \theta)-1) \\ + (2+ e \cos \theta ) \sin \theta \sin^2 i \sin 2(\omega+\theta) \end{bmatrix} \\ \\ \frac{dh}{dt} &= - \frac{3}{2} J_2 \frac{\mu R_e^2}{r^3} \sin^2 i \sin 2(\omega+\theta) \end{align} \]

 

위 미분 방정식은 J2 섭동에 의한 궤도요소의 순간적인 시간 변화율을 명시적으로 보여준다. 또한 위 식을 풀면 J2 섭동에 의해서 변화하는 궤도요소를 매 순간 마다 알 수 있다.

다음 그림은 예로서 주기가 2시간, 경사각 25도, 반장축 길이 8,059 km, 이심율 0.1714, RAAN 이 45도, 근점편각 30도인 궤도가 J2 섭동의 영향에 의해서 24시간 동안 궤도요소가 어떻게 변화하는 지를 보여준다.

 

 

위 시뮬레이션 결과에 의하면 J2 섭동은 모든 궤도요소에 작고 짧은 주기적 진동을 초래하는 것을 볼 수 있다. 이는 식 (1)의 미분 방정식에 있는 많은 삼각함수를 보면 짐작할 수 있다. 반면에 시간이 지남에 따라 \(\Omega\) 와 \(\omega\) 에는 드리프트가 생기지만 나머지 궤도요소에는 주기적 진동만 있을 뿐 장기적으로 일정한 평균값을 유지하는 것을 볼 수 있다.

이처럼 J2 섭동에 의한 궤도요소의 변화는 비주기적 장기 변동에 주기적 단기 진동이 중첩되어 있다고 정리할 수 있다. 이런 관점에서 주기적 단기 진동은 궤도요소의 평균값에서 주기적으로 벗어나는 편차다.

J2 섭동이 장기적으로 궤도에 미치는 영향을 평가하는 데 효과적인 방법은 단기 반응과 장기 반응을 분리하여 장기 반응만을 기술하도록 미분 방정식을 '평균' 형태로 만드는 것이다. 이를 위해서 평균화 방법(averaging method)를 사용한다.

\(f\) 를 궤도요소 6개 중의 하나라고 가정한다. 우주비행체가 궤도를 한바퀴 도는 동안 \(f\) 의 평균 시간 변화율을 구해보자. 평균 시간 변화율은 궤도를 1회전한 후 발생한 \(f\) 의 변화량을 1회전하는데 소요된 시간으로 나누면 된다. 따라서

 

\[ \begin{align} \left( \frac{df}{dt} \right)_{ave} = \frac{1}{T} \int_0^f \ df = \frac{1}{T} \int_0^{2\pi} \frac{df}{d \theta} \ d\theta \tag{2} \end{align} \]

 

이다. 여기서 \(\theta\) 는 실제 비행각(true anomaly)이고 \(T\) 는 1회전하는데 소요된 시간이다. 위 식을 조금 더 전개하면 다음과 같다.

 

\[ \begin{align} \left( \frac{df}{dt} \right)_{ave} = \frac{1}{T} \int_0^{2\pi} \frac{df}{dt} \frac{dt}{d\theta} \ d\theta= \frac{n}{2\pi} \int_0^{2\pi} \frac{df}{dt} \frac{1}{\dot{\theta}} \ d\theta \tag{3} \end{align} \]

 

여기서 섭동을 고려하지 않았을 때의 주기를 근사값 \(T\) 로 사용했으며 \(n\) 은 평균 회전 각속도이다.

 

\[ \begin{align} T= 2\pi \sqrt{ \frac{\mu}{a^3} }, \ \ \ \ \ n= \sqrt{\frac{\mu}{a^3}} \tag{4} \end{align} \]

 

식 (1)에 의하면 \(\dot{\theta}\) 은 다음과 같이 계산할 수 있다.

 

\[ \begin{align} \dot{\theta} &= \frac{h}{r^2} - \dot{\Omega} \cos i \tag{5} \\ \\ &= \frac{h}{r^2} \left( 1- \frac{r^2}{h} \dot{\Omega} \cos i \right) \end{align} \]

 

따라서

 

\[ \begin{align} \frac{1}{\dot{\theta}} &= \frac{r^2}{h} \left( 1- \frac{r^2}{h} \dot{\Omega} \cos i \right)^{-1} \tag{6} \\ \\ & \approx \frac{r^2}{h} \left( 1+ \frac{r^2}{h} \dot{\Omega} \cos i \right) \\ \\ & \approx \frac{r^2}{h} \end{align} \]

 

이다. 식 (6)을 (3)에 대입하면 \(f\) 의 평균 시간 변화율은 다음과 같다.

 

\[ \begin{align} \left(\frac{df}{dt} \right)_{ave} = \frac{n}{2\pi} \int_0^{2\pi} \frac{df}{dt} \frac{r^2}{h} \ d\theta \tag{7} \end{align} \]

 

평균 시간 변화율 계산은 기본적으로 모든 평균화가 궤도 운동 전체에 걸쳐 이루어진다고 가정하는 것으로 이 과정을 통해 주기적 단기 진동이 제거된다.

 

 

이제 식 (7)을 이용하여 궤도요소의 평균 시간 변화율을 계산해 보자. 이를 위해서 먼저 다음과 같은 몇 가지 삼각함수에 관한 적분이 필요하다.

 

\[ \begin{align} & \int_0^{2\pi} \cos 2(\omega+\theta) \ d\theta = \frac{1}{2} \left[ \sin 2(\omega+\theta) \right]_0^{2\pi}=0 \tag{6} \\ \\ & \int_0^{2\pi} \sin 2(\omega+\theta) \ d\theta= - \frac{1}{2} \left[ \cos 2(\omega+\theta) \right]_0^{2\pi}=0 \\ \\ & \int_0^{2\pi} \cos \theta \sin 2(\omega+\theta) \ d\theta =\frac{1}{2} \int_0^{2\pi} ( \sin (2\omega +3\theta)+ \sin (2\omega+\theta ) ) \ d\theta =0 \\ \\ & \int_0^{2\pi} \sin^2 (\omega+ \theta) \ d\theta= \frac{1}{2} \int_0^{2\pi} (1-\cos 2(\omega+\theta)) \ d\theta = \pi \\ \\ & \int_0^{2\pi} \cos \theta \sin^2 (\omega+ \theta) \ d\theta = \frac{1}{2} \int_0^{2\pi} \cos \theta (1-\cos 2(\omega+ \theta )) \ d\theta=0 \\ \\ & \int_0^{2\pi} \sin \theta \sin^2 (\omega+\theta) \ d\theta = \frac{1}{2} \int_0^{2 \pi} \sin \theta (1- \cos 2(\omega+\theta)) \ d\theta =0 \end{align} \]

 

먼저 비교적 계산이 간단한 \(\Omega\) 의 평균 시간 변화율부터 구해보자. 식 (7)과 (1)을 이용하면,

 

\[ \begin{align} \left( \frac{d\Omega }{dt} \right)_{ave} &= \frac{n}{2\pi} \int_0^{2\pi} \frac{d\Omega}{dt} \frac{r^2}{h} \ d\theta \tag{9} \\ \\ &= - \frac{n}{2\pi} \int_0^{2\pi} 3J_2 \frac{\mu R_e^2}{h^2 r } \cos i \sin^2 (\omega + \theta) \ d\theta \end{align} \]

 

이다. 여기서 \(r= \frac{ \frac{h^2}{\mu}}{1+e \cos \theta} \) 이므로

 

\[ \begin{align} \left( \frac{d\Omega }{dt} \right)_{ave} &= - \frac{3n}{2\pi }J_2 \frac{\mu^2 R_e^2}{h^4} \cos i \int_0^{2\pi} (1+e \cos \theta) \sin^2 (\omega + \theta) \ d\theta \tag{10} \\ \\ &=- \frac{3n}{2} J_2 \frac{\mu^2 R_e^2}{h^4} \cos i \end{align} \]

 

가 되는데, \( \frac{h^2}{\mu}=a(1-e^2 )\) 을 이용하면 위 식은 다음과 같이 된다.

 

\[ \begin{align} \left( \frac{d\Omega }{dt} \right)_{ave} = -\frac{3}{2} J_2 \frac{ \sqrt{\mu} R_e^2 }{a^{7/2} (1-e^2 )^2 } \cos i \tag{11} \end{align} \]

 

이번에는 \(h\) 의 평균 시간 변화율을 구해보자.

 

\[ \begin{align} \left( \frac{dh}{dt} \right)_{ave} &= \frac{n}{2\pi } \int_0^{2\pi} \frac{dh}{dt} \frac{r^2}{h} \ d\theta \tag{12} \\ \\ &=- \frac{n}{2\pi} \int_0^{2 \pi} \frac{3}{2} J_2 \frac{\mu R_e^2}{hr} \sin^2 i \sin⁡ 2(\omega+\theta) \ d\theta \\ \\ &=- \frac{3n}{4 \pi} J_2 \frac{\mu R_e^2}{h} \sin^2 i \int_0^{2\pi } \frac{1}{r} \sin⁡ 2(\omega+ \theta) \ d\theta \\ \\ &=- \frac{3n}{4\pi} J_2 \frac{\mu^2 R_e^2}{h^3} \sin^2 i \int_0^{2\pi} (1+e \cos \theta ) \sin 2(\omega+\theta) \ d\theta \\ \\ &=0 \end{align} \]

 

조금 복잡하긴 하지만 다른 궤도요소의 평균 시간 변화율도 비슷한 방법으로 계산할 수 있다.

J2 섭동에 의한 궤도요소의 평균 시간 변화율을 정리하면 다음과 같다.

 

\[ \begin{align} & \left( \frac{da}{dt} \right)_{ave}= \left( \frac{de}{dt} \right)_{ave}= \left( \frac{di}{dt} \right)_{ave}= \left( \frac{dh}{dt} \right)_{ave}=0 \tag{13} \\ \\ & \left( \frac{d\Omega}{dt} \right)_{ave}=-\frac{3}{2} J_2 \frac{ \sqrt{\mu} R_e^2 }{a^{7/2} (1-e^2 )^2 } \cos i \\ \\ & \left( \frac{d\omega}{dt} \right)_{ave} =-\frac{3}{2} J_2 \frac{ \sqrt{\mu} R_e^2 }{a^{7/2} (1-e^2 )^2 } \left( \frac{5}{2} \sin^2 i-2 \right) \\ \\ & \left( \frac{d\theta}{dt} \right)_{ave} = n+\frac{3}{4} J_2 \frac{ \sqrt{\mu} R_e^2 }{a^{7/2} (1-e^2 )^2 } (3 \sin^2 i-2) \end{align} \]

 

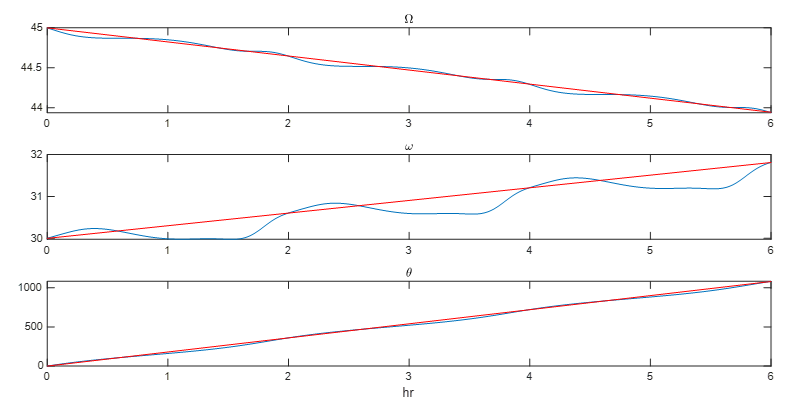
앞선 궤도 예제에 식 (13)을 적용하면 다음과 같은 시뮬레이션 결과를 얻을 수 있다. 그림은 주기의 3배인 6시간에 걸친 J2 섭동에 의한 궤도요소의 시간 변화를 보여준다. 파란색은 식 (1)에 의한 변화, 빨간색은 식 (13)에 의한 평균 변화를 나타낸다.