노이즈 공분산 추정 방법: ALS
칼만필터(Kalman filter)는 시스템의 동역학 모델과 센서의 확률적 특성을 이용하여 시스템의 상태를 추정하는 알고리즘이다 (https://pasus.tistory.com/105). 만약 시스템의 동역학 모델이 선형이고 그 모델의 오차와 센서 노이즈를 가우시안(Gaussian) 확률 함수로 정확히 표현할 수 있다면 칼만필터가 계산한 시스템의 상태 추정값은 최소평균제곱오차(MMSE, minimum mean-square error) 관점에서 최적(optimal)이다. 가우시안이 아니더라도 칼만필터는 최상(best)의 추정값을 산출한다.
하지만 실제로는 많은 상황에서 시스템 모델의 오차와 센서 노이즈의 확률적 특성을 모르거나 부분적으로만 아는 경우가 많기 때문에 부정확한 확률 특성 값을 사용한 칼만필터의 상태 추정값은 최적 또는 최상이 아닐 수 있고 심지어 발산할 수도 있다.
이 문제를 해결하기 위한 방안으로 적응(adaptive) 칼만필터에 대한 연구가 그동안 많이 진행되어 왔다. 현재 적응 칼만필터는 공학의 전 분야와 일기예보 및 계량경제학 등 다양한 분야에서 활용되고 있다.
적응 칼만필터에서 필수적인 부분은 칼만필터에서 요구되는 시스템 모델의 오차와 센서 노이즈의 확률적 특성, 정확히는 프로세스 노이즈 및 센서 노이즈의 공분산(covariance) 행렬을 식별(identification)하는 문제다. 이에 대한 연구도 많이 있는데 여기서는 2006년에 Odelson이 개발한 자기공분산최소제곱(ALS, autocovariance least-squares) 추정방법을 소개한다.
이 방법은 칼만필터의 이노베이션을 이용하여 노이즈 공분산 행렬을 추정하는 것으로서, 다른 방법보다 계산이 간단하고 제약이 적은 장점이 있다. 반면 단점도 적지 않아서 이에 대한 후속 연구도 많은 편이다. 여기서는 처음 개발된 알고리즘을 소개하며 관련 연구는 다음 논문을 참고하기 바란다.
B. Odelson, "A new autocovariance least-squares method for estimating noise covariances", Automatica, 2006.
M. Rajamani, Data-based Techniques to Improve State Estimation in Model Predictive Control, Ph.D. thesis, 2007.
L. Zhang, " On the Identification of Noise Covariances and Adaptive Kalman Filtering: A New Look at a 50 Year-Old Problem", IEEE Access, 2020.
X. Lin, "A real-time autocovariance least-squares algorithm", Digital Signal Processing, 2022.
다음과 같은 선형 시스템에 대해서
\[ \begin{align} \mathbf{x}_{t+1} &= F_t \mathbf{x}_t+ G_t \mathbf{u}_t + \Gamma_t \mathbf{w}_t \tag{1} \\ \\ \mathbf{z}_t &= H_t \mathbf{x}_t+ \mathbf{v}_t \end{align} \]
칼만필터 알고리즘은 다음과 같다 (https://pasus.tistory.com/355).
\[ \begin{align} & \hat{\mathbf{x}}_{t+1|t} = F_t \hat{\mathbf{x}}_{t|t} + G_t \mathbf{u}_t \tag{2} \\ \\ & P_{t+1|t} = F_t P_{t|t} F_t^T + \Gamma_t Q_t \Gamma_t^T \\ \\ & \nu_t = \mathbf{z}_t-H_t \hat{\mathbf{x}}_{t|t-1} \\ \\ & S_t = H_t P_{t|t-1} H_t^T+R_t \\ \\ & K_t = P_{t|t-1} H_t^T S_t^{-1} \\ \\ & \hat{\mathbf{x}}_{t|t}= \hat{\mathbf{x}}_{t|t-1}+K_t \nu_t \\ \\ & P_{t|t}= P_{t|t-1}-K_t S_t K_t^T = (I-K_t H_t ) P_{t|t-1} (I-K_t H_t )^T+ K_t R_t K_t^T \end{align} \]
식 (1)에서 행렬 \(F_t, \ G_t, \ \Gamma_t, \ H_t\) 와 프로세스 및 측정 노이즈 공분산 \(Q_t\) 와 \(R_t\) 가 모두 상수 행렬이라면 식 (1)을 시불변 시스템이라고 한다. 시불변 시스템이라고 하더라도 칼만필터 식 (2)에서 예측 공분산 \(P_{t+1|t}\) 과 갱신 공분산 \(P_{t|t}\) 는 여전히 시간의 함수이므로 칼만게인 \(K_t\) 도 시간의 함수다.
그런데 만약 일정한 조건을 만족하면 공분산이 상수 행렬로 수렴하며 그와 함께 칼만게인도 상수 행렬이 되는 것을 볼 수 있다. 이런 상태를 정정상태(steady-state)라고 한다.
상수 칼만게인을 이용하는 칼만필터를 정정상태 칼만필터(steady-state KF)라고 한다. 정정상태 칼만필터는 준최적(suboptimal) 필터이지만 공분산을 업데이트할 필요가 없고 사전에 미리 계산된 게인값을 사용하므로 계산량이 대폭 감소되는 장점이 있어 가장 많이 사용되는 칼만필터 형태다.
수학으로 풀어보는 칼만필터 알고리즘 - 예스24
수학 때문에 칼만필터에 장벽을 느끼는 이들을 위한 책!칼만필터는 수학 알고리즘이다. 따라서 수학식 없이는 칼만필터를 이해할 수도, 사용할 수도 없다. 『수학으로 풀어보는 칼만필터 알고
www.yes24.com
식 (2)에서 예측 공분산 \(P_{t+1|t}\) 과 갱신 공분산 \(P_{t|t}\) 이 각각 \(\bar{P}\) 와 \(P\) 로 수렴한다고 하면 그 식은 다음과 같다.
\[ \begin{align} & \bar{P} = FP F^T+ \Gamma Q \Gamma^T \tag{3} \\ \\ & S=H \bar{P}H^T+R \\ \\ & K= \bar{P}H^T S^{-1} \\ \\ & P= \bar{P}-KSK^T=(I-KH) \bar{P} (I-KH)^T+KRK^T \end{align} \]
그러면 정상상태 칼만필터 알고리즘은 다음과 같이 된다.
\[ \begin{align} & \hat{\mathbf{x}}_{t+1|t}=F \hat{\mathbf{x}}_{t|t} + G \mathbf{u}_t \tag{4} \\ \\ & \nu_t= \mathbf{z}_t-H \hat{\mathbf{x}}_{t|t-1} \\ \\ & \hat{\mathbf{x}}_{t|t}= \hat{\mathbf{x}}_{t|t-1}+K \nu_t \end{align} \]
즉 상수 행렬인 칼만필터 게인 \(K\) 만 필요한 것이다. 식 (3)에서 \(\bar{P}\) 와 \(P\) 를 한 개의 예측 공분산 식으로 합치면 다음과 같다.
\[ \begin{align} \bar{P} &= FPF^T+ \Gamma Q \Gamma^T \tag{5} \\ \\ &= F[ \bar{P}- \bar{P}H^T (H\bar{P}H^T+R)^{-1} H \bar{P} ] F^T+ \Gamma Q \Gamma^T \end{align} \]
위 식을 이산시간 대수 리카티 방정식(discrete-time algebraic Riccati equation)이라고 한다. 이산시간 대수 리카티 방정식은 \((F,H)\) 가 관측가능(observable)하고 (https://pasus.tistory.com/342), \((F, \Gamma \sqrt{Q})\) 가 제어가능(controllable)하면(https://pasus.tistory.com/336), 유일한 정정행렬 해 \(\bar{P} \gt 0\) 를 갖는다. 또한 이 값으로 계산한 칼만게인 \(K\) 는 \(F(I-KH)\) 를 안정(stable)하게 만든다. \(\bar{P}\) 는 다음 식으로도 표현할 수 있다.
\[ \begin{align} \bar{P} = F[(I-KH) \bar{P} (I-KH)^T+KRK^T ] F^T+ \Gamma Q \Gamma^T \tag{6} \end{align} \]
그렇다면 정정상태 칼만필터에서는 이노베이션(innovation), \(\nu_t= \mathbf{z}_t-H \hat{\mathbf{x}}_{t|t-1}\), 은 어떠한 특성을 가질까?
최적 칼만필터에서 이노베이션이 평균이 \(0\) 인 가우시안 화이트 노이즈였다면 준최적인 정정상태 칼만필터에서는 이노베이션이 평균이 \(0\) 인 정상(stationary) 가우시안 시퀀스(https://pasus.tistory.com/353)가 된다. 이를 증명해 보기로 한다.
먼저 \(\mathbb{E}[\nu_t ]=0\) 을 증명한다. 사전(a priori) 추정 오차를 \(\tilde{\mathbf{x}}_{t+1|t}= \mathbf{x}_{t+1}- \hat{\mathbf{x}}_{t+1|t}\) 로 정의하고 다음 시간스텝으로 전개하면 다음과 같다.
\[ \begin{align} \hat{\mathbf{x}}_{t+1|t} &= F \mathbf{x}_t+ G \mathbf{u}_t + \Gamma \mathbf{w}_t-( F \hat{\mathbf{x}}_{t|t} +G \mathbf{u}_t ) \tag{7} \\ \\ &= F \mathbf{x}_t+ \Gamma \mathbf{w}_t-F \left( \hat{\mathbf{x}}_{t|t-1}+K (H \mathbf{x}_t+ \mathbf{v}_t-H \hat{\mathbf{x}}_{t|t-1} ) \right) \\ \\ &= (F-FKH) \tilde{\mathbf{x}}_{t|t-1}+ \Gamma \mathbf{w}_t-FK \mathbf{v}_t \\ \\ &= \bar{F} \tilde{\mathbf{x}}_{t|t-1}+ \Gamma \mathbf{w}_t-FK \mathbf{v}_t \end{align} \]
여기서
\[ \begin{align} \bar{F}=F-FKH \tag{8} \end{align} \]
이다. 따라서 평균 전파식은
\[ \begin{align} \mathbb{E}[ \tilde{\mathbf{x}}_{t+1|t} ] = \bar{F} \ \mathbb{E}[ \tilde{\mathbf{x}}_{t|t-1} ] \tag{9} \end{align} \]
이 되는데 칼만게인 \(K\) 는 위 시스템을 안정하게 만드므로 \(\mathbb{E}[ \tilde{\mathbf{x}}_{t+1|t} ]=0\) 으으로 점근적으로 수렴한다. 한편 이노베이션을 전개해 보면,
\[ \begin{align} \nu_t &= \mathbf{z}_t-H \hat{\mathbf{x}}_{t|t-1} \tag{10} \\ \\ &=H \mathbf{x}_t+ \mathbf{v}_t-H \hat{\mathbf{x}}_{t|t-1} \\ \\ &=H \tilde{\mathbf{x}}_{t|t-1}+ \mathbf{v}_t \end{align} \]
이므로 \(\mathbb{E}[\nu_t ]=H \mathbb{E}[ \tilde{\mathbf{x}}_{t|t-1} ]=0\) 이 된다.
이번에는 정상(stationary) 가우시안 시퀀스가 됨을 증명한다. 이전 게시글 (https://pasus.tistory.com/355)에 의하면 이노베이션의 자기공분산은 다음과 같이 계산된다.
\[ \begin{align} \mathbb{E}[\nu_t \nu_i^T ]=H_t \Phi_{t,i} P_{i|i-1} H_i^T-H_t \Phi_{t,i+1} F_i K_i R_i \tag{11} \end{align} \]
여기서 \(H_t, H_i \to H\), \(F_i \to F\), \(K_i \to K\), \(R_i \to R\), \(\Phi_{t,i} \to \bar{F}^{t-i}\), \(P_{i|i-1} \to \bar{P}\) 로 치환하면, 정정상태 칼만필터의 이노베이션의 자기공분산은 다음과 같이 된다.
\[ \begin{align} \mathbb{E}[\nu_t \nu_i^T ]=H \bar{F}^{t-i} \bar{P}H^T-H\bar{F}^{t-i-1} FKR \tag{12} \end{align} \]
식 (12)에 의하면 이노베이션의 자기공분산은 시간차 \((t-i)\) 만의 함수다. 따라서 이노베이션은 평균이 \(0\) 이고 자기공분산이 시간차에만 의존하므로 정상 시퀀스라는 것을 알 수 있다. 또한 모든 확률 함수가 가우시안이고 시스템이 선형이므로 이노베이션도 가우시안이다. 이로써 이노베이션이 정상 가우시안 시퀀스라는 것이 증명되었다.
이제 이노베이션의 자기공분산은 시간차 만의 함수이므로 시간스텝 하첨자를 \(t \to t+n\), \(i \to t\) 로 변경한다. 그러면 이노베이션의 자기공분산 식 (12)는 다음과 같이 시간차 \(n\) 으로 나타낼 수 있다.
\[ \begin{align} \mathbb{E}[\nu_{t+n} \nu_t^T ]=H \bar{F}^n \bar{P}H^T-H\bar{F}^{n-1} FKR \tag{13} \end{align} \]
시간차 \(0\) 부터 시작하여 \(N\) 까지 이노베이션의 자기공분산을 \( \mathcal{R}(N) \in \mathbb{R}^{n_z N \times n_z}\) 으로 표기하자. 식 (13)을 이용하면 다음과 같이 \(\mathcal{R}(N)\) 을 계산할 수 있다.
\[ \begin{align} \mathcal{R}(N) &= \mathbb{E} \begin{bmatrix} \nu_t \nu_t^T \\ \nu_{t+1} \nu_t^T \\ \vdots \\ \nu_{t+N-1} \nu_t^T \end{bmatrix}= \begin{bmatrix} H\bar{P}H^T+R \\ H\bar{F}\bar{P}H^T-HFKR \\ \vdots \\ H\bar{F}^{N-1} \bar{P}H^T-H\bar{F}^{N-2} FKR \end{bmatrix} \tag{14} \\ \\ & = \begin{bmatrix} H \\ H \bar{F} \\ \vdots \\ H \bar{F}^{N-1} \end{bmatrix} \bar{P}H^T + \begin{bmatrix} I \\ -HFK \\ \vdots \\ -H\bar{F}^{N-2} FK \end{bmatrix} R \end{align} \]
이제 시스템의 운동 모델 (1)에서 \(F, \ \Gamma ,\ H\) 는 정확히 알고 모델의 확률적 부분인 \(Q\) 와 \(R\) 만 모른다고 가정한다. 그리고 정정상태 칼만필터의 게인 \(K\) 를 부정확한 확률 정보에 바탕을 둔 \(Q_f\) 와 \(R_f\) 를 이용하여 설계했다고 가정한다.
그러면 식 (14)에서 \(K\) 는 아는 값이므로 \(\mathcal{R}(N)\) 은 \(\bar{P}\) 와 \(R\) 만의 함수다. 또한 식 (6)에 의하면 \(\bar{P}\) 는 \(Q\) 와 \(R\) 의 함수이므로 \(\mathcal{R}(N)\) 은 시스템의 확률 정보인 \(Q\) 와 \(R\) 만의 함수가 된다. 따라서 정정상태 칼만필터가 산출한 시간차 \(0\) 부터 시작하여 \(N\) 까지의 이노베이션 자기공분산인 \(\mathcal{R}(N)\) 을 알 수만 있다면 식 (6)과 (14)를 이용하여 \(Q\) 와 \(R\) 을 계산해 낼 수 있다.
크로넥커 곱과 벡터화 기법 (https://pasus.tistory.com/354)을 이용하여 식 (14)를 벡터화시키면 다음과 같다.
\[ \begin{align} \mbox{vec}(\mathcal{R}(N)) &= \mbox{vec}(\mathcal{O} \bar{P}H^T )+ \mbox{vec}(\mathcal{T}R) \tag{15} \\ \\ &= (H \otimes \mathcal{O}) \mbox{vec}(\bar{P} )+ (I \otimes \mathcal{T}) \mbox{vec}(R) \end{align} \]
여기서 \(\mathcal{O} \in \mathbb{R}^{n_z N \times n_x} \) 와 \(\mathcal{T} \in \mathbb{R}^{n_z N \times n_z }\) 는 각각 다음과 같다.
\[ \begin{align} \mathcal{O} = \begin{bmatrix} H \\ H \bar{F} \\ \vdots \\ H \bar{F}^{N-1} \end{bmatrix}, \ \ \ \ \ \mathcal{T} = \begin{bmatrix} I \\ -HFK \\ \vdots \\ -H\bar{F}^{N-2} FK \end{bmatrix} \tag{16} \end{align} \]
이제 식 (6)을 백터화시키면 다음과 같다.
\[ \begin{align} \mbox{vec}(\bar{P} )=(\bar{F} \otimes \bar{F} )\mbox{vec}(\bar{P} )+(FK \otimes FK) \mbox{vec}(R)+(\Gamma \otimes \Gamma )\mbox{vec}(Q) \tag{17} \end{align} \]
식 (17)에서 \(\mbox{vec}(\bar{P} )\) 를 계산한 후 식 (15)에 대입하면 다음과 같다.
\[ \begin{align} \mbox{vec}( \mathcal{R}(N))= \begin{bmatrix} A_Q & A_R \end{bmatrix} \begin{bmatrix} \mbox{vec}(Q) \\ \mbox{vec}(R) \end{bmatrix} =A_{QR} X_{QR} \tag{18} \end{align} \]
여기서
\[ \begin{align} A_Q &= (H \otimes \mathcal{O}) (I-\bar{F} \otimes \bar{F} )^{-1} (\Gamma \otimes \Gamma) \\ \\ A_R &= (H \otimes \mathcal{O}) (I-\bar{F} \otimes \bar{F} )^{-1} (FK \otimes FK)+(I \otimes \mathcal{T}) \end{align} \]
이다. 식 (18)에서 각 행렬의 차원을 보면 \(\mbox{vec}(\mathcal{R}(N)) \in \mathbb{R}^{n_z^2 N}\), \(A_{QR} \in \mathbb{R}^{n_z^2 N \times (n_w^2+n_z^2)}\), \(X_{QR} \in \mathbb{R}^{(n_w^2+n_z^2 ) \times 1}\) 이므로 \(n_z^2 N \ge (n_w^2+n_z^2)\) 이 되도록 \(N\) 을 선택하면 \(X_{QR}\), 즉 \(Q\) 와 \(R\) 을 최소제곱(LS) 방법으로 다음과 같이 추정할 수 있다.
\[ \begin{align} \hat{X}_{QR}=(A_{QR}^T A_{QR} )^{-1} A_{QR}^T \mbox{vec}(\mathcal{R}(N)) \tag{19} \end{align} \]
이제 \(\mathcal{R}(N)\) 을 계산하는 일만 남았다. 실제 이노베이션 시퀀스 데이터로 \(\mathcal{R}(N)\) 을 계산하기 위해서는 시간 평균과 앙상블 평균이 동일하다는 에르고딕(ergodic) 가정이 필요하다. 즉,
\[ \begin{align} \mathcal{R}(N)= \mathbb{E} \begin{bmatrix} \nu_t \nu_t^T \\ \nu_{t+1} \nu_t^T \\ \vdots \\ \nu_{t+N-1} \nu_t^T \end{bmatrix} = \left< \begin{bmatrix} \nu_t \nu_t^T \\ \nu_{t+1} \nu_t^T \\ \vdots \\ \nu_{t+N-1} \nu_t^T \end{bmatrix} \right> \tag{20} \end{align} \]
여기서 \(\lt \ \gt\) 기호는 시퀀스 데이터의 시간 평균을 의미한다. 시간 평균에 사용되는 이노베이션 데이터는 정정상태 데이터만 사용한다. 즉 초기 과도 기간을 지나 출력이 정정상태에 도달한 이후에 수집한다. 문헌에 의하면 이노베이션 시퀀스 데이터를 이용하여 자기공분산을 계산하는 방법이 몇 가지 나와 있는데 여기서는 그 중 두가지를 소개한다.
먼저 첫번째 방법은 이노베이션 시퀀스를 \(N_d\) 개, \(\{ \nu_1, \ \nu_2, ... , \nu_{N_d} \}\), 수집한다. 데이터 개수 \(N_d\) 는 시간 시프트 \(N\) 보다 크게 잡는다. 그리고 다음 식으로 시간 평균을 계산한다.
\[ \begin{align} \lt \nu_{t+d} \nu_t^T \gt = \frac{1}{N_d-d} \sum_{j=1}^{N_d-d} \nu_{j+d} \nu_j^T , \ \ \ \ \ d=0, ..., N-1 \tag{21} \end{align} \]
이 방법은 시간 시프트 \(d\) 가 커질수록 시간 평균에 사용되는 데이터 수가 감소한다는 특징이 있다.

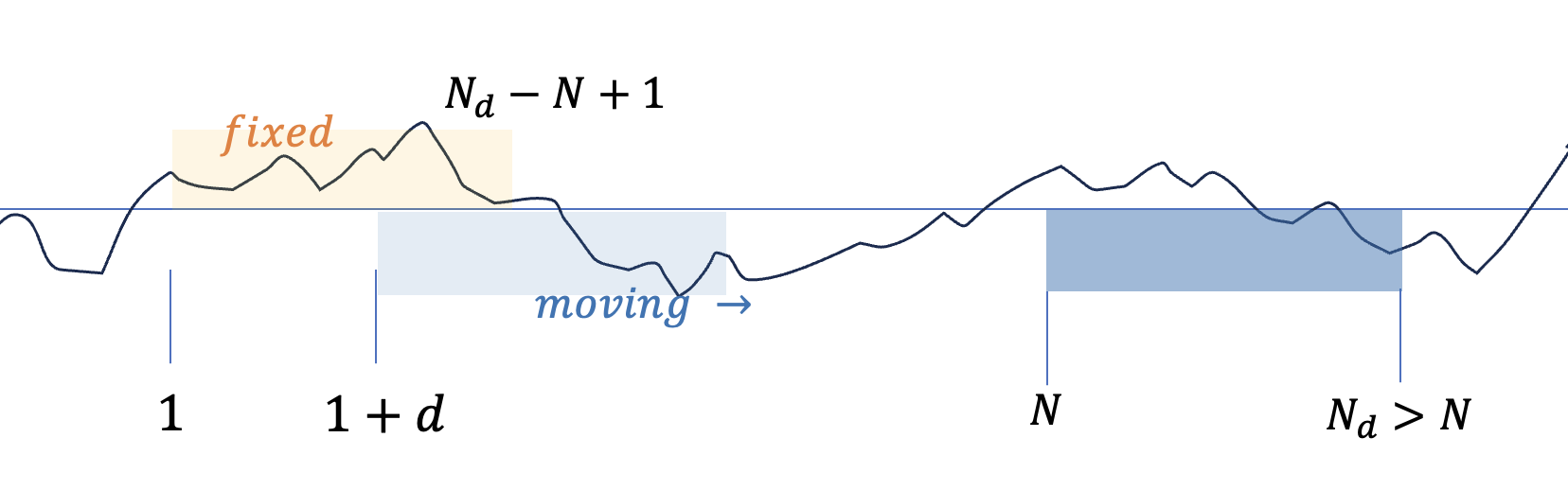
두번쨰 방법은 시간 평균에 사용되는 데이터 수를 고정시키는 방법으로서 다음 식으로 시간 평균을 계산한다.
\[ \begin{align} \left< \begin{bmatrix} \nu_t \nu_t^T \\ \nu_{t+1} \nu_t^T \\ \vdots \\ \nu_{t+N-1} \nu_t^T \end{bmatrix} \right> = \frac{1}{N_d-N+1} \begin{bmatrix} \nu_1 \nu_1^T+ \nu_2 \nu_2^T+ \cdots + \nu_{N_d-N+1} \nu_{N_d-N+1}^T \\ \nu_2 \nu_1^T+\nu_3 \nu_2^T+ \cdots +\nu_{N_d-N+2} \nu_{N_d-N+1}^T \\ \vdots \\ \nu_N \nu_1^T+\nu_{N+1} \nu_2^T+ \cdots +\nu_{N_d } \nu_{N_d-N+1}^T \end{bmatrix} \tag{22} \end{align} \]
지금까지 ALS 알고리즘에 대해서 설명했는데 이 방법의 단점은 다음과 같다. 먼저 \(Q\) 와 \(R\) 을 추정할 수 있는 조건이 불분명하다는 점이다. 정정상태 칼만필터의 조건을 충족하더라도 \(Q\) 와 \(R\) 을 추정할 수 없는 경우도 있다. 두번째는 \(Q\) 와 \(R\) 이 대칭행렬인데 수식에서 이를 강제할 방법이 없다는 것이고, 세번째는 오프라인 후처리 방식이어서 실시간에서는 사용할 수 없다는 점이다. 네번째는 자기공분산을 계산할 때 시간차 \(N\) 이 지나치게 클 경우 계산 효율성이 떨어질 수도 있다. 또한 이와 관련된 대부분의 알고리즘에 해당하는 단점으로서 모델 파라미터 \(F, G \)등을 식별할 수 없다는 점도 들 수 있겠다.