[Continuous-Time] 경로 제약조건이 있는 최적제어 문제

일반적인 최적제어 문제 (https://pasus.tistory.com/231)는 초기 및 최종 상태변수 등식 제약조건과 운동방정식을 만족하면서 목적함수를 최소화하는 제어입력을 결정하는 문제였다.

 

\[ \begin{align} \min J = \phi ( & \mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) + \int_{t_0}^{t_f} g(\mathbf{x}(t), \mathbf{u}(t), t) \ dt \tag{1} \\ \\ \mbox{ subject to : } \ & \dot{\mathbf{x}} (t)= \mathbf{f}( \mathbf{x}(t), \mathbf{u}(t), t) \\ \\ & \psi (\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f )=0 \end{align} \]

 

여기서 \(\mathbf{x}(t) \in \mathbb{R}^n\) 는 상태변수 벡터, \(\mathbf{u}(t) \in \mathbb{R}^p\) 는 제어입력 벡터이고, \(t\) 는 연속시간 (continuous-time), \(t_0\) 는 초기시간(initial time), \(t_f\) 는 최종시간(final time), \(g( \mathbf{x}(t), \mathbf{u}(t), t)\) 는 운행비용(running cost), \(\phi \in \mathbb{R}^1\) 는 초기시간과 최종시간에서의 비용, \(\psi \in \mathbb{R}^m\) 는 초기 및 최종 상태변수 등식 제약조건이다.

이제 일반적인 최적제어 문제를 조금 확장하여 상태변수와 제어입력의 함수로 된 경로 제약조건(path constraint)을 포함시켜 보자. 경로제약 조건은 전체 시간구간 \( \ t_0 \le t \le t_f\) 에 걸쳐 만족되어야 하며 상태변수 뿐만 아니라 제어입력에 관한 제약도 포함되어 있다.

경로 제약조건 \(\mathbf{c} \in \mathbb{R}^r\) 는 다음과 같이 다양하게 등식 제약조건 및 부등식 제약조건으로 주어질 수 있다.

 

\[ \begin{align} & \mathbf{c}(\mathbf{x}(t), \mathbf{u}(t), t)=0 \tag{2} \\ \\ & \mathbf{c}(\mathbf{u}(t), t)=0 \\ \\ & \mathbf{c}( \mathbf{x}(t), t)=0 \\ \\ & \mathbf{c}(\mathbf{x}(t), \mathbf{u}(t), t) \le 0 \tag{3} \\ \\ & \mathbf{c}(\mathbf{u}(t), t) \le 0 \\ \\ & \mathbf{c}( \mathbf{x}(t), t) \le 0 \end{align} \]

 

여기서 경로 제약조건의 차원 \(r\) 은 제어입력의 차원 \(p\) 보다 작다고 가정한다. 즉, \(r \lt p\).

만약 \(r=p\) 라면 제어입력은 경로 제약조건에 의해서만 정해지므로 최적화 여지가 없어지며, \(r \gt p\) 라면 경로 제약조건 마저 충족시키지 못하게 된다.

식 (2)와 (3)에 의하면 경로 제약조건은 상태변수와 제어입력이 각각 제약조건에 명시적으로 포함되는 지의 여부에 따라서 세 가지 유형으로 나누어짐을 알 수 있다.

 

 

먼저 등식 제약조건 식 (2)에서 상태변수와 제어입력이 제약조건에 명시적으로 포함되어 있는 \(\mathbf{c}( \mathbf{x}(t), \mathbf{u}(t),t)=0\) 부터 시작한다. 등식 제약조건은 전체 시간구간의 매 순간마다 만족되어야 하므로 라그랑지 곱수(Lagrange multiplier) \(\mu\) 를 도입하여 운동방정식과 함께 목적함수에 포함시켜야 한다.

 

\[ \begin{align} J & = \phi ( \mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) + \nu^T \psi (\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) \tag{4} \\ \\ & \ \ + \int_{t_0}^{t_f} \begin{bmatrix} g(\mathbf{x}(t), \mathbf{u}(t), t) + \lambda^T \left( \mathbf{f}( \mathbf{x}(t), \mathbf{u}(t), t)- \dot{\mathbf{x}} \right) \\ + \mu^T \mathbf{c}( \mathbf{x}(t), \mathbf{u}(t), t) \end{bmatrix} \ dt \end{align} \]

 

여기서 \(\lambda\) 와 \(\nu\) 는 각각 운동방정식과 초기 및 최종 상태변수 등식 제약조건에 연결된 라그랑지 곱수다. 그러면 해밀토니안(Hamiltonian) 함수는 다음과 같이 바뀐다.

 

\[ \begin{align} \mathcal{H}( \mathbf{x}, \mathbf{u}, \lambda, \mu, t) = g(\mathbf{x}, \mathbf{u}, t) + \lambda^T \mathbf{f}( \mathbf{x}, \mathbf{u}, t) + \mu^T \mathbf{c}( \mathbf{x}, \mathbf{u}, t) \tag{5} \end{align} \]

 

따라서 최적제어의 필요조건(necessary condition)도 다음과 같이 변경된다.

 

\[ \begin{align} \dot{\mathbf{x}} & = \frac{ \partial \mathcal{H}}{ \partial \lambda} = \mathbf{f} ( \mathbf{x} , \mathbf{u}, t) \tag{6} \\ \\ - \dot{\lambda} & =\frac{ \partial \mathcal{H}}{ \partial \mathbf{x}}= \left( \frac{\partial \mathbf{f}}{\partial \mathbf{x}} \right)^T \lambda + \frac{\partial g}{\partial \mathbf{x} }+ \left( \frac{ \partial \mathbf{c}}{\partial \mathbf{x} } \right)^T \mu \\ \\ 0 & = \frac{ \partial \mathcal{H}}{ \partial \mathbf{u} } = \left( \frac{ \partial \mathbf{f}}{\partial \mathbf{u}} \right)^T \lambda + \frac{\partial g}{\partial \mathbf{u}}+ \left( \frac{ \partial \mathbf{c}}{\partial \mathbf{u} } \right)^T \mu \end{align} \]

 

식 (6)의 세 번째 식인 정정조건(stationary condition)에 의하면 라그랑지 곱수 \(\mu\) 는 다음과 같이 계산할 수 있다.

 

\[ \begin{align} \mu = - \left[ \left( \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \right)^T \right]^ + \left[ \left( \frac{\partial \mathbf{f}}{ \partial \mathbf{u} } \right)^T \lambda + \frac{\partial g}{\partial \mathbf{u}} \right] \tag{7} \end{align} \]

 

여기서 \( \left[ \left( \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \right)^T \right]^ + \) 은 \( \left( \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \right)^T \in \mathbb{R}^{p \times r} \) 의 유사 역행렬(pseudo inverse matrix)으로서 다음과 같이 주어진다 (https://pasus.tistory.com/310).

 

\[ \begin{align} \left[ \left( \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \right)^T \right]^+ = \left[ \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \left( \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \right)^T \right]^{-1} \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \tag{8} \end{align} \]

 

등식 제약조건 식 (2)에서 두번째 유형인 제어입력만 명시적으로 제약조건에 포함된 \( \mathbf{c}( \mathbf{u}(t), t)=0\) 의 경우에는 식 (6)을 다음과 같이 수정하면 된다.

 

\[ \begin{align} \dot{\mathbf{x}} & = \frac{ \partial \mathcal{H}}{ \partial \lambda} = \mathbf{f} ( \mathbf{x} , \mathbf{u}, t) \tag{9} \\ \\ - \dot{\lambda} & =\frac{ \partial \mathcal{H}}{ \partial \mathbf{x}}= \left( \frac{\partial \mathbf{f}}{\partial \mathbf{x}} \right)^T \lambda + \frac{\partial g}{\partial \mathbf{x} } \\ \\ 0 & = \frac{ \partial \mathcal{H}}{ \partial \mathbf{u} } = \left( \frac{ \partial \mathbf{f}}{\partial \mathbf{u}} \right)^T \lambda + \frac{\partial g}{\partial \mathbf{u}}+ \left( \frac{ \partial \mathbf{c}}{\partial \mathbf{u} } \right)^T \mu \end{align} \]

 

만약 식 (2)의 세번째 유형인 \(\mathbf{c}( \mathbf{x}(t), t)=0\) 과 같이 상태변수만 제약조건에 있다면 문제가 조금 복잡해 진다. 먼저 경로 제약조건을 목적함수에 포함시켜 보자.

 

\[ \begin{align} J & = \phi ( \mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) + \nu^T \psi (\mathbf{x}(t_0 ), \mathbf{x}(t_f ), t_0, t_f ) \tag{10} \\ \\ & \ \ + \int_{t_0}^{t_f} \begin{bmatrix} g(\mathbf{x}(t), \mathbf{u}(t), t) + \lambda^T \left( \mathbf{f}( \mathbf{x}(t), \mathbf{u}(t), t)- \dot{\mathbf{x}} \right) \\ + \mu^T \mathbf{c}( \mathbf{x}(t), t) \end{bmatrix} \ dt \end{align} \]

 

그러면 해밀토니안은 다음과 같이 된다.

 

\[ \begin{align} \mathcal{H}( \mathbf{x}, \mathbf{u}, \lambda, \mu, t) = g(\mathbf{x}, \mathbf{u}, t) + \lambda^T \mathbf{f}( \mathbf{x}, \mathbf{u}, t) + \mu^T \mathbf{c}( \mathbf{x}, t) \tag{11} \end{align} \]

 

여기서 문제는 제어입력의 섭동(perturbation)에 대해서 경로 제약조건이 변하지 않는데 있다.

 

\[ \begin{align} \Delta \mathbf{c}( \mathbf{x}(t), t) = \left( \frac{ \partial \mathbf{c}}{\partial \mathbf{x}} \right)^T \Delta \mathbf{x} + \frac{ \partial \mathbf{c}}{\partial t} \Delta t \tag{12} \end{align} \]

 

그러면 경로 제약조건이 식 (6) 또는 (9)의 정정조건에 아무런 영향도 못 미치게 된다. 정정조건은 최적 제어입력을 계산하는 식이다.

 

\[ \begin{align} 0 = \frac{\partial \mathcal{H}}{\partial \mathbf{u}} &= \left( \frac{\partial \mathbf{f}}{\partial \mathbf{u}} \right)^T \lambda + \frac{ \partial g}{\partial \mathbf{u} } + \left( \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \right)^T \mu \tag{13} \\ \\ &= \left( \frac{\partial \mathbf{f}}{\partial \mathbf{u}} \right)^T \lambda + \frac{ \partial g}{\partial \mathbf{u} } \end{align} \]

 

이 문제를 해결하기 위해서 상태변수만으로 되어 있는 경로 제약조건을 시간 미분해 본다.

 

\[ \begin{align} \frac{d \mathbf{c}( \mathbf{x}(t), t)}{dt} &= \frac{\partial \mathbf{c}}{ \partial t} +\left( \frac{\partial \mathbf{c}}{\partial \mathbf{x}} \right)^T \frac{d \mathbf{x}}{dt} \tag{14} \\ \\ & =\frac{\partial \mathbf{c}}{ \partial t} +\left( \frac{\partial \mathbf{c}}{\partial \mathbf{x}} \right)^T \mathbf{f}(\mathbf{x}, \mathbf{u}, t) \\ \\ &= \mathbf{c}^{(1)} ( \mathbf{x}(t), \mathbf{u}(t), t) = 0 \end{align} \]

 

만약 식 (14)에서 제어입력 \(\mathbf{u}\) 가 명시적으로 나타나면 식 (14)는 식 (2)의 첫번째 유형과 같이 상태변수와 제어입력이 모두 포함된 제약조건 역할을 하게 된다. 원래 제약조건 \(\mathbf{c}\) 를 \(0\)차 등식 제약조건으로 정의한다면 \(\frac{d \mathbf{c}}{dt}\) 는 \(1\)차 등식 제약조건에 해당하며 이를 표시하기 위해서 식 (14)의 \(\mathbf{c}^{(1)}\) 과 같이 위첨자 \((1)\)을 사용했다. 경로 제약조건이 \(0\)차에서 \(1\)차로 바뀌었으므로 원래 경로 제약조건인 \(0\)차 제약조건 \(\mathbf{c}(\mathbf{x}(t),t)=0\) 은 경로상의 한 시점에서만 만족하면 된다.

 

\[ \begin{align} \mathbf{c}( \mathbf{x}(t_0 ), t_0 )=0 \ \ \ \ \mbox{or} \ \ \ \ \mathbf{c}(\mathbf{x}(t_f ), t_f )=0 \tag{15} \end{align} \]

 

만약 식 (14)에서 제어입력 \(\mathbf{u}\) 가 명시적으로 나타나지 않는다면 \(\mathbf{u}\) 가 명시적으로 나타날 때까지 시간 미분을 계속한다. 만약 \(m\)번째 미분에서 나타났다면 \(m\)차 등식 제약조건은 다음과 같이 된다.

 

\[ \begin{align} \mathbf{c}^{(m)} ( \mathbf{x}(t), \mathbf{u}(t), t)=0, \ \ \ \ \ \mathbf{c}^{(m)}= \frac{d^m \mathbf{c}( \mathbf{x}(t), t)}{dt^m } \tag{16} \end{align} \]

 

이 경우 식 (15)에 해당하는 경계조건은 다음 식으로 바뀐다.

 

\[ \begin{align} \begin{bmatrix} \mathbf{c}( \mathbf{x}(t), t) \\ \mathbf{c}^{(1)}( \mathbf{x}(t), t) \\ \vdots \\ \mathbf{c}^{(m)}( \mathbf{x}(t), t) \end{bmatrix}=0 \ \ \ \ \ @ \ t=t_0 \ \ \ \mbox{or} \ \ \ t=t_f \tag{17} \end{align} \]

 

이번에는 식 (3)으로 주어지는 부등식 경로 제약조건에 대한 최적제어 문제를 고려해 보자. 부등식 경로 제약조건은 항상 전체 경로에 걸쳐 적용되는 것은 아니다. 제약조건의 영향을 받는 구간도 있고 그렇지 않은 구간도 있다.

 

 

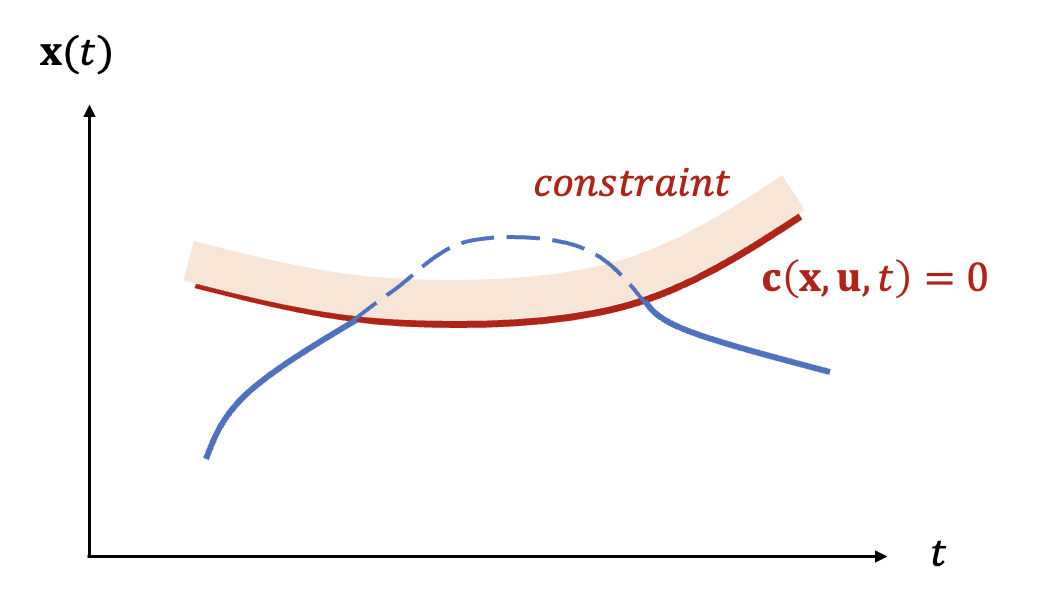
시간이 변화하면서 다른 경로 제약조건이 부과되기도 한다.

 

 

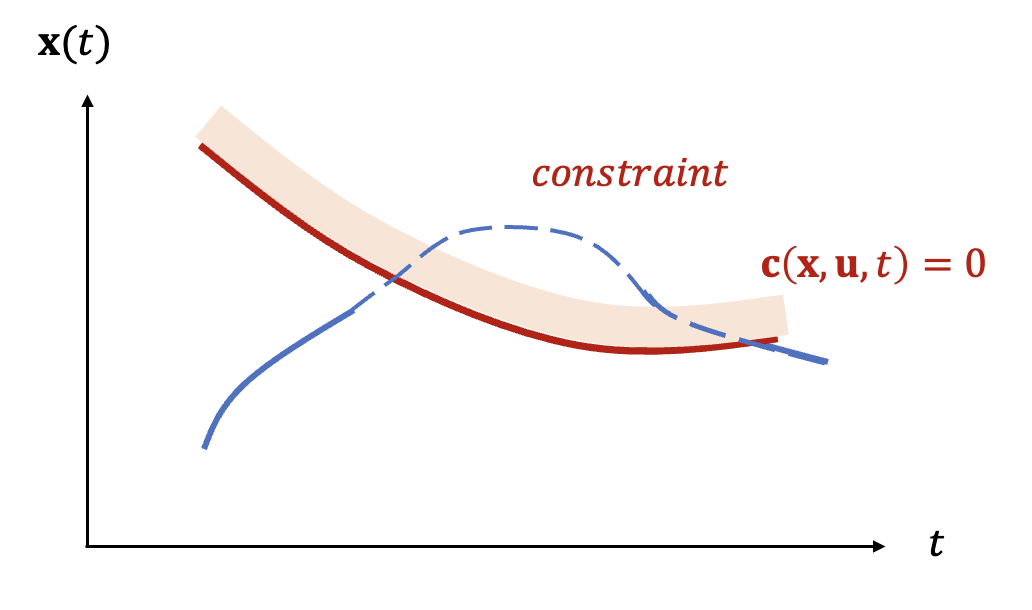
또한 어떤 제약조건은 저절로 만족되기도 한다.

 

 

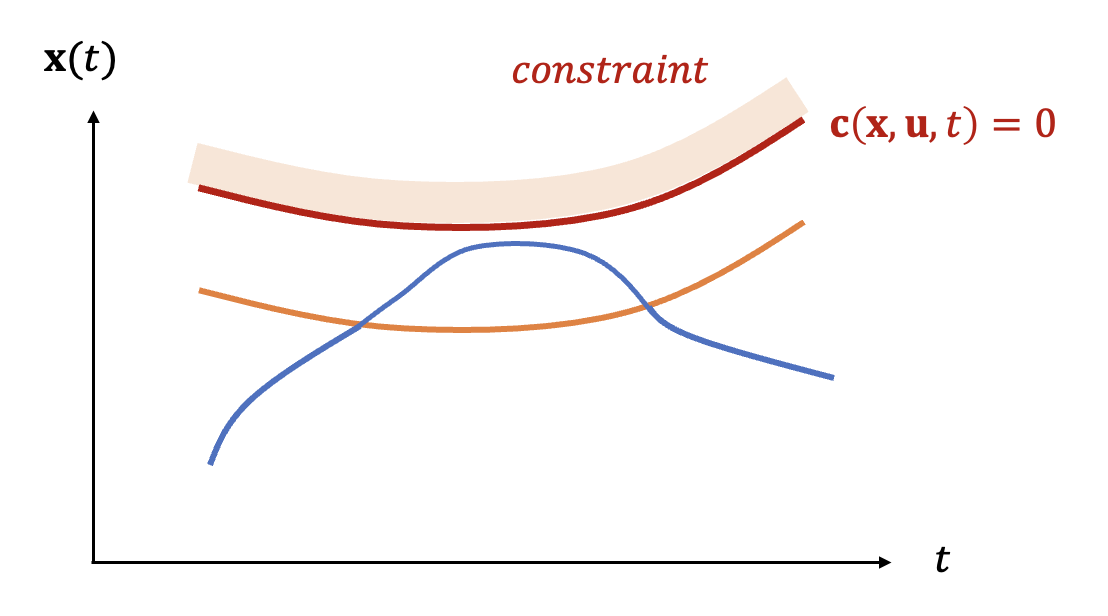
먼저 식 (3)에서 첫번째 유형인 \(\mathbf{c}( \mathbf{x}(t), \mathbf{u}(t), t) \le 0\) 부터 시작한다. 등식 제약조건의 경우와 마찬가지로 해밀토니안을 다음과 같이 정의한다.

 

\[ \begin{align} \mathcal{H}( \mathbf{x}, \mathbf{u}, \lambda, \mu, t) = g(\mathbf{x}, \mathbf{u}, t) + \lambda^T \mathbf{f}( \mathbf{x}, \mathbf{u}, t) + \mu^T \mathbf{c}( \mathbf{x}, \mathbf{u}, t) \tag{18} \end{align} \]

 

부등식 제약조건이 있는 경우에는 KKT 조건(Karush-Kuhn-Tucker conditions)을 만족해야 한다 (https://pasus.tistory.com/73). 따라서 식 (6)의 정정조건 이외에 두가지 추가 조건이 더 필요하다.

 

\[ \begin{align} & 0= \frac{\partial \mathcal{H}}{\partial \mathbf{u}} = \left( \frac{\partial \mathbf{f}}{\partial \mathbf{u}} \right)^T \lambda + \frac{ \partial g}{\partial \mathbf{u} } + \left( \frac{\partial \mathbf{c}}{\partial \mathbf{u}} \right)^T \mu \tag{19} \\ \\ & \mu \ge 0 , \ \ \ \mbox{if } \ \mathbf{c}(\mathbf{x}(t), \mathbf{u}(t), t)=0 \\ \\ & \mu=0, \ \ \ \mbox{if } \ \mathbf{c}(\mathbf{x}(t), \mathbf{u}(t), t) \lt 0 \end{align} \]

 

식 (19)의 추가조건은 각각 dual constraint와 complementary slackness에 해당한다. 식 (3)의 두번째와 세번째 유형에 대해서도 등식 제약조건의 경우와 비슷한 방법을 적용할 수 있다.