[INS] 관성항법 방정식 (Kinematics of Inertial Navigation)
관성항법시스템 (INS, inertial navigation system)은 관성센서인 가속도계와 자이로스코프에서 측정된 가속도(specific force, 단위 질량당 힘)와 각속도를 이용하여 운동체의 위치, 속도, 자세를 추정하는 항법시스템의 한 종류다. 관성항법시스템은 단독으로 위치, 속도, 자세를 추정할 수 있기 때문에 외부 센서나 신호를 사용할 수 없거나 또는 신뢰할 수 없는 상황, 예를 들면 수중이나 지하에서 특히 유용하다.
관성항법의 구현 방식에는 운동체의 회전 운동과 기계적으로 분리된 짐벌(Gimbal)에 관성센서를 장착하는 짐벌 (Gimbaled INS) 방식과, 운동체에 관성센서를 직접 부착하는 스트랩다운 (Strapdown INS) 방식으로 나눌 수 있다. 최신 관성항법시스템은 대부분 스트랩다운 방식을 사용한다. 관성항법 운동학 방정식은 관성 좌표계로 표현된 뉴턴의 운동법칙을 항법 좌표계로 좌표 변환한 식으로 관성항법 알고리즘의 근간을 이룬다.
관성항법시스템의 기준 좌표계인 항법 좌표계로는 운동체의 질량 중심점을 원점으로 하거나 또는 그 점의 위치를 지표면에 투사한 점을 원점으로 하고, x축을 북쪽, y축을 동쪽, z축을 지구 중력가속도 방향으로 정의하는 이동 로컬 탄젠트(moving local tangent) 좌표계 또는 NED(North-East-Down) 좌표계를 사용한다 (https://pasus.tistory.com/179). 이 좌표계는 좌표계의 원점이 어디에 위치 하느냐에 따라 좌표계의 축 방향이 달라지는 국지적(local) 좌표계다.

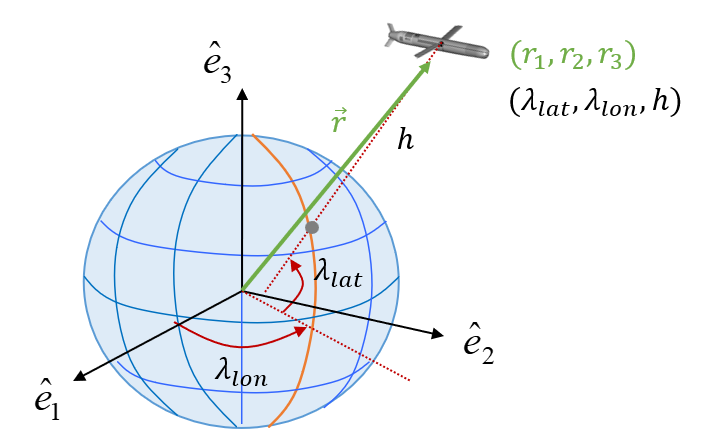
위 그림은 지구 중심이 원점인 ECI(Earth Centered Inertial) 좌표계 \(\{i\}\) 와 ECEF(Earth Centered Earth Fixed) 좌표계 \(\{e\}\) 를 보여준다 (https://pasus.tistory.com/179). \(\omega_{ie}\) 는 지구의 자전 각속력로서 WGS84 데이터에 의하면 \(\omega_{ie}=7.291151467 \times 10^{-5} \ rad/sec\) 이다. 벡터 \(\vec{r}\) 이 지구 중심에서 운동체의 질량중심까지의 위치벡터라고 하면 \(\vec{r}\) 을 ECI 좌표계로 표현한 벡터 \(\mathbf{r}^i\) 과 ECEF 좌표계로 표현한 벡터 \(\mathbf{r}^e\) 는 다음과 같은 관계가 있다.
\[ \mathbf{r}^i=C_e^i \mathbf{r}^e \tag{1} \]
여기서 \(C_e^i\) 는 ECI 좌표계에서 ECEF 좌표계로의 DCM이다 (https://pasus.tistory.com/83). 식 (1)의 양변을 시간 미분하면 다음과 같다.
\[ \begin{align} \dot{\mathbf{r}}^i &= \dot{C}_e^i \mathbf{r}^e+C_e^i \dot{\mathbf{r}}^e \tag{2} \\ \\ &= C_e^i [\omega_{ie}^e \times ] \mathbf{r}^e+C_e^i \dot{\mathbf{r}}^e \end{align} \]
여기서 \(\omega_{ie}^e\) 는 지구의 자전에 의한 회전 각속도를 ECEF 좌표계로 표현한 벡터다. 다시 식 (2)의 양변을 시간 미분하면 ECI 좌표계에서의 가속도벡터와 ECI 좌표계에서의 가속도벡터 관계식을 얻을 수 있다.
\[ \begin{align} \ddot{\mathbf{r}}^i &= \dot{C}_e^i [\omega_{ie}^e \times ] \mathbf{r}^e+C_e^i [ \dot{\omega}_{ie}^e \times ] \mathbf{r}^e+C_e^i [\omega_{ie}^e \times ] \dot{\mathbf{r}}^e+ \dot{C}_e^i \mathbf{r} ̇^e+C_e^i \ddot{\mathbf{r}}^e \tag{3} \\ \\ &=C_e^i [\omega_{ie}^e \times ]^2 \mathbf{r}^e+2C_e^i [\omega_{ie}^e \times ] \dot{\mathbf{r}}^e+C_e^i \ddot{\mathbf{r}}^e \end{align} \]
여기서 지구의 자전 각속력은 일정하기 때문에 \(\omega_{ie}^e=0\) 이다. 운동체의 속도는 ECEF 기준, 즉 지면 기준의 상대적인 속도이므로 항법 좌표계 \(\{n\}\) 에서의 속도벡터 \(\mathbf{v}^n\) 은 다음과 같이 정의된다.
\[ \begin{align} \mathbf{v}^n \equiv C_e^n \dot{\mathbf{r}}^e \tag{4} \end{align} \]
식 (2)와 (3)을 이용하면 식 (4)의 미분식은 다음과 같이 된다.
\[ \begin{align} \dot{\mathbf{v}}^n &= \dot{C}_e^n \dot{\mathbf{r}}^e+C_e^n \ddot{\mathbf{r}}^e \tag{5} \\ \\ &= C_e^n [\omega_{ne}^e \times ] \dot{\mathbf{r}}^e+C_e^n \ddot{\mathbf{r}}^e \\ \\ &= -[\omega_{en}^n \times ] C_e^n \dot{\mathbf{r}}^e+C_e^n \left( C_i^e \ddot{\mathbf{r}}^i-[\omega_{ie}^e \times ]^2 \mathbf{r}^e-2[ \omega_{ie}^e \times ] \dot{\mathbf{r}}^e \right) \end{align} \]
여기서 \(C_e^n [\omega_{ne}^e \times ]=-[\omega_{en}^n \times ] C_e^n\) 임을 이용하였다. 참고로 이 관계식은 \(C_e^n C_n^e=I\) 의 양변을 미분하여 증명할 수 있다.
\[ \begin{align} & \dot{C}_e^n C_n^e+C_e^n \dot{C}_n^e=0 \tag{6} \\ \\ \to \ & C_e^n [\omega_{ne}^e \times ] C_n^e=-C_e^n C_n^e [\omega_{en}^n \times ] \\ \\ \to \ & C_e^n [\omega_{ne}^e \times ]= -[\omega_{en}^n \times ] C_e^n \end{align} \]
식 (5)와 (6)에서 \(\omega_{en}^n\) 은 ECEF 좌표계에 대한 항법 좌표계의 각속도벡터 \(^e \vec{\omega}^n\) 을 항법 좌표계로 표현한 벡터다.
운동체의 운동 반경이 작다면 NED 좌표계의 원점을 지표면에 고정시키는 경우도 있다. 만약 항법 좌표계가 지표면에 고정되어 있다면 지구와 함께 자전한다는 점에서 ECEF 좌표계와 같다. 이 경우 ECEF 좌표계에 대한 NED 좌표계의 각속도벡터는 0 이므로 \(\omega_{en}^n=0\) 이다.
관성 좌표계에서는 뉴턴 제2법칙이 성립하므로 운동체의 가속도는 운동체에 가해지는 단위 질량당 힘과 중력의 합과 같다.
\[ \begin{align} \ddot{\mathbf{r}}^i= \mathbf{f}^i+ \mathbf{g}^i \tag{7} \end{align} \]
여기서 \(\mathbf{f}^i\) 는 운동체의 질량중심에 가해지는 단위 질량당 외력을, \(\mathbf{g}^i\) 는 중력 가속도를 각각 ECI 좌표계로 표현한 벡터다. 식 (7)을 식 (5)에 대입하고 전개하면 다음과 같이 된다.
\[ \begin{align} \dot{\mathbf{v}}^n &= -[\omega_{en}^n \times ] C_e^n \dot{\mathbf{r}}^e+C_i^n ( \mathbf{f}^i+\mathbf{g}^i )-C_e^n \left( [\omega_{ie}^e \times ]^2 \mathbf{r}^e+2[ \omega_{ie}^e \times ] \dot{\mathbf{r}}^e \right) \tag{8} \\ \\ &=-[ \omega_{en}^n \times ] C_e^n \dot{\mathbf{r}}^e+ \mathbf{f}^n+ \mathbf{g}^n-[\omega_{ie}^n \times ]^2 \mathbf{r}^n-2[ \omega_{ie}^n \times ] C_e^n \dot{\mathbf{r}}^e \\ \\ &=-([\omega_{en}^n \times ]+2[ \omega_{ie}^n \times ]) \mathbf{v}^n+C_b^n \mathbf{f}^b+( \mathbf{g}^n-[\omega_{ie}^n \times]^2 \mathbf{r}^n ) \\ \\ &= -([ \omega_{en}^n \times ]+2[\omega_{ie}^n \times]) \mathbf{v}^n+C_b^n \mathbf{f}^b+ \mathbf{g}_{ER}^n \end{align} \]
여기서 \(\mathbf{g}_{ER}^n= \mathbf{g}^n-[\omega_{ie}^n \times]^2 \mathbf{r}^n\) 으로서 운동체의 위치에 따라 달라지는 명목 중력 가속도이다. 명목 중력 가속도는 지구 중력 가속도와 지구의 자전에 의해서 발생하는 원심 가속도의 합으로 주어진다.

원심 가속도는 운동체가 위치하는 위도와 고도의 함수이기 때문에 명목 중력 가속도는 중력 가속도와 위도 및 위치의 함수다. WGS84의 중력 모델에 의하면 명목 중력 가속도는 다음과 같이 표현할 수 있다.
\[ \begin{align} & \mathbf{g}_{ER}^n= \begin{bmatrix} \xi g \\ -\eta g \\ g \end{bmatrix} \tag{9} \\ \\ & g=g_{eq} (1+g_1 \sin^2 \lambda_{lat} +g_2 h+g_3 h \sin^2 \lambda_{lat}+ g_4 h^2+g_5 h^2 \sin^2 \lambda_{lat} ) \\ & g_{eq}=9.7803267714 \ m/sec^2 \\ & g_1=0.00193185138639+ \frac{e_{er}^2}{2} \\ & g_2=- \frac{(2+e_{er}^2+f_{er})}{R_{eq}} \\ & g_3=g_1 g_2+2 \frac{e_{er}^2}{R_{eq}} \\ & g_4= \frac{3}{R_{eq}^2} \\ & g_5=g_1 g_4 \\ & e_{er}=0.0818191908426, \ \ f_{er}=0.003449786, \ \ R_{eq}=6378137 \ m \end{align} \]
여기서 \(\lambda_{lat}\) 는 위도, \(R_{eq}\) 는 적도 반지름, \(e_{er}\) 는 지구 이심율, \(f_{er}\) 는 지구 평평도다. 지구가 균일한 타원체를 따른다면 로컬 중력 벡터 방향은 타원체 표면에 대해 수직이 될 것이다. 하지만 중력은 지구의 불균일한 질량 분포로 인해 위치에 따라 달라지는데 이러한 중력 벡터의 크기와 방향이 계산된 값에서 벗어나는 것을 중력 이상이라고 한다. 식 (9)에서 \(\xi\) 와 \(\eta\) 는 중력 이상을 표현하기 위한 것으로서 로컬 중력 벡터가 로컬 수직 방향으로부터 벗어난 미세 각을 의미한다. \(\xi\) 는 북쪽 방향, \(\eta\) 는 동쪽 방향으로 측정한 각이다.

식 (8)에서 \(C_b^n\) 는 항법 좌표계에서 동체 좌표계로의 DCM이며, 동체 좌표계 \(\{b\}\) 는 운동체의 질량중심점을 원점으로 하는 운동체에 부착한 좌표계다. \(\mathbf{f}^b\) 는 동체 좌표계로 표현된 단위 질량당 외력으로서 운동체의 질량중심점에 부착된 가속도계가 측정하는 값이다.
한편, 항법 좌표계에서 위치벡터의 미분방정식은 \(\mathbf{r}^n=C_e^n \mathbf{r}^e\) 를 미분하여 구할 수 있다.
\[ \begin{align} \dot{\mathbf{r}}^n &= \dot{C}_e^n \mathbf{r}^e+C_e^n \dot{\mathbf{r}}^e \tag{10} \\ \\ &=C_e^n [ \omega_{ne}^e \times ] \mathbf{r}^e+C_e^n \dot{\mathbf{r}}^e \\ \\ &= -[\omega_{en}^n \times ] C_e^n \mathbf{r}^e+ \mathbf{v}^n \\ \\ &=-[\omega_{en}^n \times ] \mathbf{r}^n+ \mathbf{v}^n \end{align} \]
항법 좌표계에 대한 동체 좌표계의 자세를 나타내는 \(C_b^n\) 의 미분방정식은 다음과 같다.
\[ \begin{align} \dot{C}_b^n &= C_b^n [\omega_{nb}^b \times ] \tag{11} \\ \\ &=C_b^n [\omega_{ib}^b \times]-[ \omega_{in}^n \times] C_b^n \end{align} \]
참고로 위 식의 두번째 줄은 다음과 같이 증명할 수 있다.
\[ \begin{align} & C_n^i C_b^n C_i^b=I \tag{12} \\ \\ \to \ & \dot{C}_n^i C_b^n C_i^b+C_n^i \dot{C}_b^n C_i^b+C_n^i C_b^n \dot{C}_i^b=0 \\ \\ \to \ & C_n^i [\omega_{in}^n \times ]C_b^n C_i^b+C_n^i C_b^n [\omega_{nb}^b \times ]C_i^b+C_n^i C_b^n C_i^b [\omega_{bi}^i \times ]=0 \\ \\ \to \ & C_n^i [\omega_{in}^n \times ] C_b^n C_i^b+C_n^i C_b^n [\omega_{nb}^b \times]C_i^b-C_n^i C_b^n [\omega_{ib}^b \times ]C_i^b=0 \\ \\ \to \ & C_b^n [\omega_{nb}^b \times ]=C_b^n [\omega_{ib}^b \times ]-[\omega_{in}^n \times ]C_b^n \end{align} \]
여기서 \(\omega_{ib}^b\) 는 ECI 좌표계에 대한 동체 좌표계의 각속도벡터 \(^i \vec{\omega}^b\) 를 동체 좌표계로 표현한 벡터로서 운동체의 부착된 자이로스코프가 측정하는 값이다.
식 (11)에서 각속도벡터는 각각 다음과 같이 계산할 수 있다.
\[ \begin{align} \omega_{nb}^b &= \omega_{ib}^b- \omega_{in}^b \tag{13} \\ \\ &= \omega_{ib}^b-(C_b^n )^T \omega_{in}^n \\ \\ &= \omega_{ib}^b-(C_b^n )^T (\omega_{ie}^n+\omega_{en}^n ) \end{align} \]
식 (8), (10), (11)을 NED 좌표계에서의 관성항법 방정식이라고 한다.
그런데 NED 좌표계가 지표면에 고정된 것이 아니라면 관성항법 방정식을 NED 좌표계보다는 위도, 경도, 높이로 주어지는 LLH (Latitude-Longitude-Height) 좌표계의 변수로 표현하는 것이 더 편리하다 (https://pasus.tistory.com/187).
우선 ECEF와 NED 좌표계 사이의 DCM은 다음과 같다.
\[ \begin{align} C_n^e &=C(z,\lambda_{lon} ) C \left(y, -\frac{\pi}{2}-\lambda_{lat} \right) \tag{14} \\ \\ &= \begin{bmatrix} -\cos \lambda_{lon} \sin \lambda_{lat} & -\sin \lambda_{lon} & -\cos \lambda_{lon} \cos \lambda_{lat} \\ - \sin \lambda_{lon} \sin \lambda_{lat} & \cos \lambda_{lon} & - \sin \lambda_{lon} \cos \lambda_{lat} \\ \cos \lambda_{lat} & 0 & -\sin \lambda_{lat} \end{bmatrix} \end{align} \]
그러면 식 (13)의 \(\omega_{ie}^n\) 은 다음과 같이 LLH 좌표계의 변수로 표현할 수 있다.
\[ \begin{align} \omega_{ie}^n &= C_e^n \omega_{ie}^e \tag{15} \\ \\ &=(C_n^e )^T \begin{bmatrix} 0 \\ 0 \\ \omega_{ie} \end{bmatrix} \\ \\ &= \begin{bmatrix} \omega_{ie} \cos \lambda_{lat} \\ 0 \\ - \omega_{ie} \sin \lambda_{lat} \end{bmatrix} \end{align} \]
\(\omega_{en}^n\) 은 다음과 같이 계산할 수 있다.
\[ \begin{align} \omega_{en}^n &=C^T \left(y, -\frac{\pi}{2}-\lambda_{lat} \right) \left( \begin{bmatrix} 0 \\ - \dot{\lambda}_{lat} \\ 0 \end{bmatrix}+C^T (z, \lambda_{lon} ) \begin{bmatrix} 0 \\ 0 \\ \dot{\lambda}_{lon} \end{bmatrix} \right) \tag{16} \\ \\ &= \begin{bmatrix} -\sin \lambda_{lat} & 0 & \cos \lambda_{lat} \\ 0 & 1 & 0 \\ - \cos \lambda_{lat} & 0 & -\sin \lambda_{lat} \end{bmatrix} \begin{bmatrix} 0 \\ - \dot{\lambda}_{lat} \\ \dot{\lambda}_{lon} \end{bmatrix} \\ \\ &= \begin{bmatrix} \dot{\lambda}_{lon} \cos \lambda_{lat} \\ -\dot{\lambda}_{lat} \\ - \dot{\lambda}_{lon} \sin \lambda_{lat} \end{bmatrix} \end{align} \]
여기서 \(\lambda_{lon}\) 는 경도다. 만약 항법 좌표계가 지표면에 고정되어 있다면 \(\omega_{en}^n=0\) 이다.
운동체의 위치벡터를 ECEF 좌표계로 표현한 벡터 \(\mathbf{r}^e\) 를 위도, 경도, 높이로 표현하면 다음과 같다 (https://pasus.tistory.com/187).
\[ \begin{align} \mathbf{r}^e = \begin{bmatrix} (R_{tr}+h) \cos \lambda_{lat} \cos \lambda_{lon} \\ (R_{tr}+h) \cos \lambda_{lat} \sin \lambda_{lon} \\ (R_{tr} (1-e_{er}^2 )+h) \sin \lambda_{lat} \end{bmatrix} \tag{17} \end{align} \]
여기서 \(R_{tr}\) 는 접선 반경(tangential radius)으로서
\[ \begin{align} R_{tr}= \frac{R_{eq}}{ \sqrt{1-e_{er}^2 \sin^2 \lambda_{lat} } } \tag{18} \end{align} \]
이다.
방향코사인행렬, 오일러각, 그리고 쿼터니언 | 박성수 | 딥웨이브- 교보ebook
이 책에서는 방향코사인행렬, 오일러각, 쿼터니언과 이들의 시간 변화율에 대해서 공부합니다. 모두 3차원 공간 상에서 어떤 기준 좌표계에 대해서 운동하는 강체의 상대적인 자세의 변화를 표
ebook-product.kyobobook.co.kr
\(\mathbf{v}^n\) 을 LLH 변수로 표현하기 위해서 식 (17)을 미분하고 식 (14)식을 이용하면 다음과 같이 계산할 수 있다 (https://pasus.tistory.com/187).
\[ \begin{align} & \mathbf{v}^n = C_e^n \dot{\mathbf{r}}^e \tag{19} \\ \\ \to \ & \begin{bmatrix} v_N \\ v_E \\ v_D \end{bmatrix} = \begin{bmatrix} \dot{\lambda}_{lat} (R_{mr}+h) \\ \dot{\lambda}_{lon} (R_{tr}+h) \cos \lambda_{lat} \\ -\dot{h} \end{bmatrix} \end{align} \]
여기서 \(R_{mr}\) 은 자오선 반경(meridian radius)으로서
\[ \begin{align} R_{mr}= \frac{R_{eq} (1-e_{er}^2 )}{(1-e_{er}^2 \sin^2 \lambda_{lat} )^{\frac{3}{2} } } \tag{20} \end{align} \]
이다. 식 (19)에 의하면 위도, 경도, 높이의 변화율은 다음과 같다.
\[ \begin{align} & \dot{\lambda}_{lat}= \frac{v_N}{(R_{mr}+h) } \tag{21} \\ \\ & \dot{\lambda}_{lon}= \frac{v_E}{(R_{tr}+h) \cos \lambda_{lat}} \\ \\ & \dot{h}=-v_D \end{align} \]
관성항법 방정식을 블록 다이어그램으로 표시하면 다음과 같다.
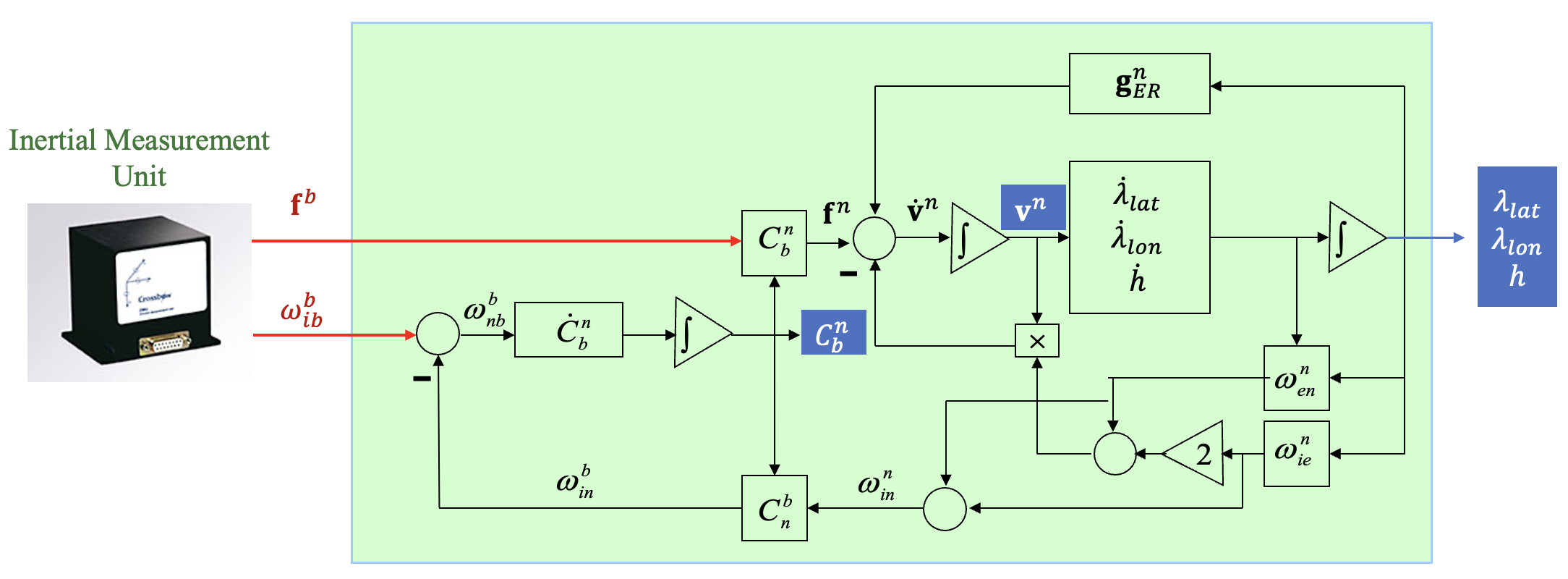
관성항법시스템은 항법 계산을 시작할 때 운동체의 초기 위치, 속도 및 자세에 대한 정확한 지식이 있어야 한다. 그런 다음 관성 측정값을 사용하여 이후 발생하는 위치, 속도 및 자세 변화의 추정치를 얻을 수 있다.