좌표변환과 관성행렬 (Inertia Matrix)
관성 다이아딕(inertia dyadic)은 특정 좌표계와 무관하지만 관성 다이아딕을 특정 좌표계로 표현한 관성행렬(inertia matrix)은 좌표계에 따라 달라진다.
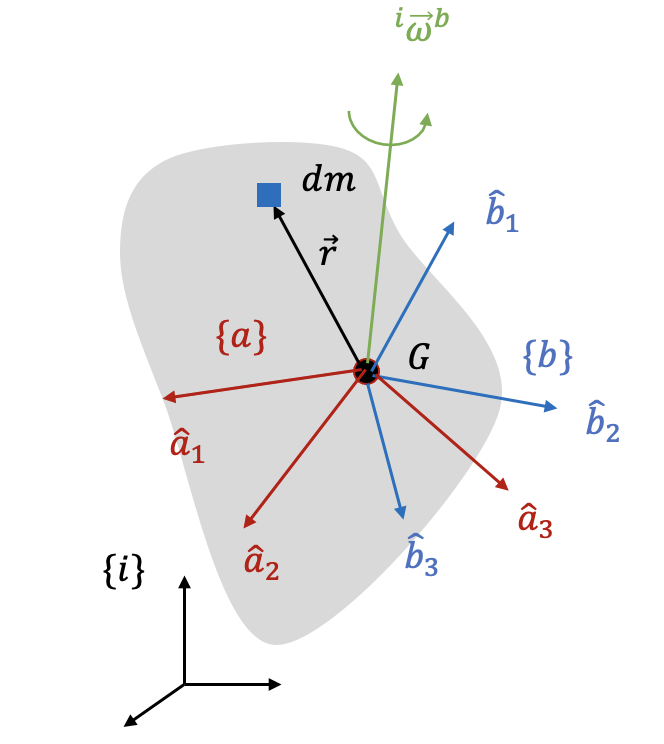
어떤 강체의 질량중심 \(G\) 를 원점으로 하고 강체에 고정된 좌표계 \(\{a\}\) 와 좌표계 \(\{b\}\) 가 있다고 하자. 질량중심 \(G\) 에 관한 관성 다이아딕 \(\bar{I}_G\) 를 좌표계 \(\{a\}\) 와 좌표계 \(\{b\}\) 로 각각 표현하면 다음과 같다 (https://pasus.tistory.com/191).
\[ \begin{align} \bar{I}_G &= \sum_{i=1}^3 \sum_{j=1}^3 I_{ij}^a \ \hat{a}_i \hat{a}_j \tag{1} \\ \\ &= \sum_{k=1}^3 \sum_{m=1}^3 I_{km}^b \ \hat{b}_k \hat{b}_m \tag{2} \end{align} \]
여기서 좌표계 \(\{a\}\) 와 좌표계 \(\{b\}\) 에 관한 관성행렬 또는 관성텐서(inertia tensor)는 각각 다음과 같다.
\[ \begin{align} & [I_G^a ]=[I_{ij}^a] \tag{3} \\ \\ & [I_G^b ]=[I_{km}^b] \end{align} \]
그렇다면 두 개의 좌표계에 관한 관성행렬 \([I_G^a ]\) 와 \([I_G^b]\) 는 어떤 관계가 있을까.
식 (1)에서 좌표계 \(\{a\}\) 의 좌표축 단위벡터는 좌표계 \(\{b\}\) 로 다음과 같이 표현할 수 있다.
\[ \hat{a}_i= \sum_{k=1}^3 (\hat{a}_i \cdot \hat{b}_k ) \hat{b}_k \tag{4} \]
식 (4)를 식 (1)에 대입하면 다음과 같다.
\[ \bar{I}_G = \sum_{i=1}^3 \sum_{j=1}^3 I_{ij}^a \left( \sum_{k=1}^3 (\hat{a}_i \cdot \hat{b}_k ) \hat{b}_k \right) \left( \sum_{m=1}^3 (\hat{a}_j \cdot \hat{b}_m ) \hat{b}_m \right) \tag{5} \]
여기서 두 좌표계의 방향코사인행렬(DCM, direction cosine matrix)의 정의에 의하면 (https://pasus.tistory.com/83),
\[ C_b^a= \begin{bmatrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix} = \begin{bmatrix} \hat{a}_1 \cdot \hat{b}_1 & \hat{a}_1 \cdot \hat{b}_2 & \hat{a}_1 \cdot \hat{b}_3 \\ \hat{a}_2 \cdot \hat{b}_1 & \hat{a}_2 \cdot \hat{b}_2 & \hat{a}_2 \cdot \hat{b}_3 \\ \hat{a}_3 \cdot \hat{b}_1 & \hat{a}_3 \cdot \hat{b}_2 & \hat{a}_3 \cdot \hat{b}_3 \end{bmatrix} \tag{6} \]
이므로, 식 (5)는 다음과 같이 쓸 수 있다.
\[ \begin{align} \bar{I}_G &= \sum_{i=1}^3 \sum_{j=1}^3 I_{ij}^a \left( \sum_{k=1}^3 C_{ik} \hat{b}_k \right) \left( \sum_{m=1}^3 C_{jm} \hat{b}_m \right) \tag{7} \\ \\ &= \sum_{k=1}^3 \sum_{m=1}^3 \left( \sum_{i=1}^3 \sum_{j=1}^3 I_{ij}^a C_{ik} C_{jm} \right) \hat{b}_k \hat{b}_m \end{align} \]
식 (7)과 (2)를 비교해 보면
\[ \begin{align} I_{km}^b &= \sum_{i=1}^3 \sum_{j=1}^3 I_{ij}^a \ C_{ik} \ C_{jm} \tag{8} \\ \\ &= \sum_{i=1}^3 \sum_{j=1}^3 C_{ki}^T \ I_{ij}^a \ C_{jm} \end{align} \]
임을 알 수 있다. 식 (6)을 이용하여 위 식을 식 (3)의 관성행렬 형태로 표현하면 다음과 같다.
\[ [I_G^b ]=(C_b^a )^T [I_G^a ] C_b^a \tag{9} \]
또는
\[ [I_G^a ]=C_b^a [I_G^b ] (C_b^a )^T \]
이다. 관성행렬은 텐서이므로 좌표변환 행렬이 두 번 사용되었다.
좌표변환에 따른 관성행렬의 변환 관계식은 다른 방법을 통해서 유도할 수도 있다. 강체의 질량중심 \(G\) 에 대한 강체의 각운동량 \(\vec{H}_G\) 는 다음과 같이 쓸 수 있다.
\[ \vec{H}_G= \bar{I}_G \cdot ^i \vec{\omega}^b \tag{10} \]
위 식을 좌표계 \(\{b\}\) 로 표현하면 다음과 같다.
\[ \begin{align} \vec{H}_G &= \sum_{j=1}^3 \sum_{k=1}^3 I_{jk}^b \ \hat{b}_j \hat{b}_k \cdot ( \omega_1 \hat{b}_1+ \omega_2 \hat{b}_2+ \omega_3 \hat{b}_3 ) \tag{11} \\ \\ &= \sum_{j=1}^3 \hat{b}_j \ (I_{j1}^b \omega_1+I_{j2}^b \omega_2+I_{j3}^b \omega_3) \end{align} \]
식 (11)을 벡터/행렬 형식으로 표현하면 다음과 같이 된다.
\[ H_G^b=[I_G^b ] \ \omega_{ib}^b \tag{12} \]
DCM \(C_b^a\) 를 이용하면 \(H_G^b\) 와 \(\omega_{ib}^b\) 를 다음과 같이 좌표계 \(\{a\}\) 로 표현할 수 있다.
\[ H_G^b=(C_b^a )^T H_G^a, \ \ \ \ \omega_{ib}^b=(C_b^a )^T \omega_{ib}^a \tag{13} \]
식 (13)을 (12)에 대입하면 다음과 같다.
\[ (C_b^a )^T H_G^a=[I_G^b ] (C_b^a )^T \omega_{ib}^a \tag{14} \]
양변에 \(C_b^a\) 를 곱하면 다음과 같이 된다.
\[ \begin{align} H_G^a &=C_b^a [I_G^b ] (C_b^a )^T \omega_{ib}^a \tag{15} \\ \\ &=[I_G^a ] \omega_{ia}^a \end{align} \]
두 좌표계 \(\{a\}\) 와 \(\{b\}\) 는 모두 강체에 고정되어 있으므로 \(^i \vec{\omega}^a = {^i \vec{\omega}^b} \) 이다. 따라서 위 식으로부터 식 (9)와 동일한 결과를 얻을 수 있다.
\[ [I_G^a ]=C_b^a [I_G^b ] (C_b^a )^T \tag{16} \]