중력 포텐셜 함수 (Gravity Potential Function)

이체문제(two-body problem)는 두 질점 사이에 작용하는 중력과 그에 따른 운동에 관한 문제다. 질량 분포가 구대칭인 구체(sphere)라면 모든 질량이 구체의 중심에 집중되어 있는 질점(point mass)처럼 작용하므로 이체문제의 가정에 부합한다.

하지만 대부분의 천체의 경우 기하학적 구조와 질량 분포는 불규칙하다. 지구도 모양이 구형이 아니라 타원체에 가깝고 밀도 또한 균일하지 않다. 이런 상황에서는 저궤도 위성의 경우 불균일한 중력의 영향 떄문에 궤도 섭동을 겪게 된다. 따라서 궤도의 장기적인 예측을 위해서는 지구를 단순하게 질점으로 가정하는 대신 중력 포텐셜 함수에 중력의 불균일한 요인을 추가하여 일정 수준의 정확도를 갖는 중력 모델을 개발할 필요가 있다.

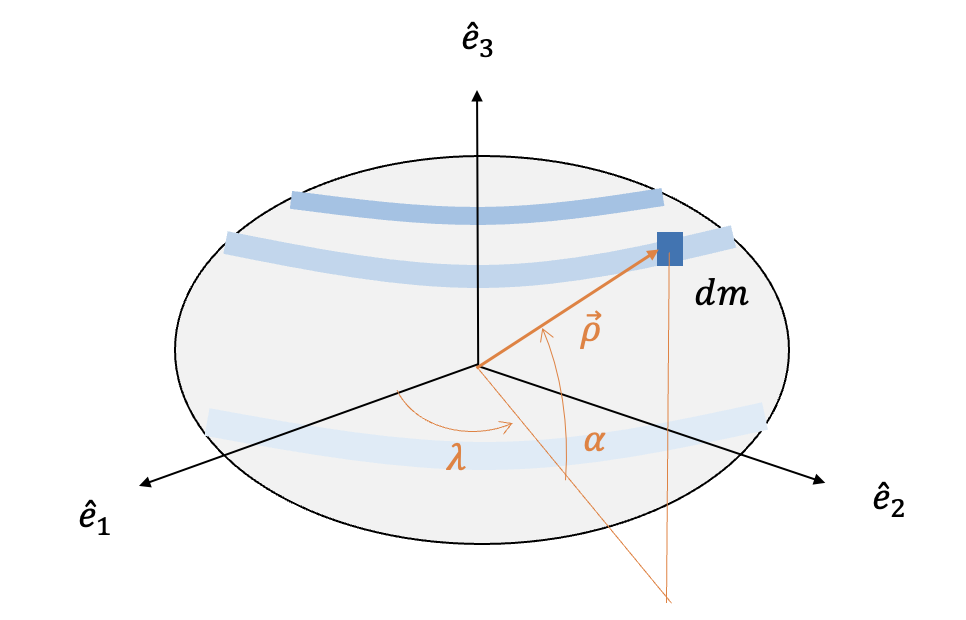
다음 그림과 같이 임의의 모양과 밀도를 갖는 천체를 가정한다. 그림에서 \(dm\) 은 천체를 구성하는 미소(infinitesimal) 질점, \(P\) 는 천체 밖에 존재하는 임의의 위치, \(\vec{\rho}\) 는 천체의 질량 중심에서 미소 질점까지의 거리 벡터, \(\vec{d}\) 는 미소 질점에서 위치 \(P\) 까지의 거리 벡터, \(\vec{r}\) 은 질량 중심에서 위치 \(P\) 까지의 거리 벡터, \(\gamma\) 는 벡터 \(\vec{r}\) 과 \(\vec{\rho}\) 의 사잇각이다.

 

 

그러면 질점 \(dm\) 에 의해서 위치 \(P\) 에 미치는 단위질량 당 미소 중력 포텐셜 함수는 다음과 같이 표현할 수 있다.

 

\[ \begin{align} dV=-\frac{Gdm}{d} \tag{1} \end{align} \]

 

여기서 \(G\) 는 만유인력 상수이고 \(d\) 는 \(\vec{d}\) 의 크기다. 코사인법칙에 의해서 \(d^2=r^2+\rho^2-2\rho r \cos \gamma\) 이므로 \(d\) 는 다음과 같이 계산할 수 있다.

 

\[ \begin{align} d=r \left( 1-2 \left( \frac{\rho}{r} \right) \cos \gamma + \left( \frac{\rho}{r} \right)^2 \right)^{1/2} \tag{2} \end{align} \]

 

식 (2)를 (1)에 대입하면 미소 중력 포텐셜 함수는 다음과 같이 된다.

 

\[ \begin{align} dV = -\frac{Gdm}{r} \left( 1-2 \left( \frac{\rho}{r} \right) \cos \gamma + \left( \frac{\rho}{r} \right)^2 \right)^{-1/2} \tag{3} \end{align} \]

 

식 (3)은 다음과 같이 르장드르 다항식(Legendre polynomials)으로 표현할 수 있다 (https://pasus.tistory.com/320).

 

\[ \begin{align} dV=-\frac{Gdm}{r} \sum_{k=0}^\infty \left( \frac{\rho}{r} \right)^k P_k (\cos \gamma ), \ \ \ \lvert \frac{\rho}{r} \rvert \lt 1 \tag{4} \end{align} \]

 

여기서 \(P_k (\cos \gamma )\) 는 \(k\) 차(degree) 르장드르 다항식이다. 위 식을 천체의 전 질량에 대해서 적분하면 다음과 같이 중력 포텐셜 함수를 얻을 수 있다.

 

\[ \begin{align} V(\vec{r}) &= - \frac{G}{r} \sum_{k=0}^\infty \iiint \left( \frac{\rho}{r} \right)^k P_k (\cos \gamma ) \ dm \tag{5} \\ \\ &= -\frac{GM}{r}- \frac{G}{r} \sum_{k=1}^\infty \iiint \left( \frac{\rho}{r} \right) ^k P_k (\cos \gamma ) \ dm \end{align} \]

 

여기서 \(P_0 (\cos \gamma )=1\) 임을 이용하였고, \(M\) 은 천체의 총 질량이다.

식 (5)는 임의의 모양과 밀도 분포를 갖는 천체에 대해서 성립하는 식이다. 위 식에 의하면 \(k\) 가 커질 수록 \( \left( \frac{\rho}{r} \right)^k\) 항은 \(0\) 으로 수렴하므로 일정 \(k\) 값 이하는 절삭함으로써 일정 수준의 정확도로 중력 포텐셜 함수를 근사화할 수 있다. 또한 \(r \to \infty\) 일 수록 \(\frac{GM}{r}\) 항이 우세해지기 때문에 임의의 천체를 질점으로 간주할 수 있다.

 

 

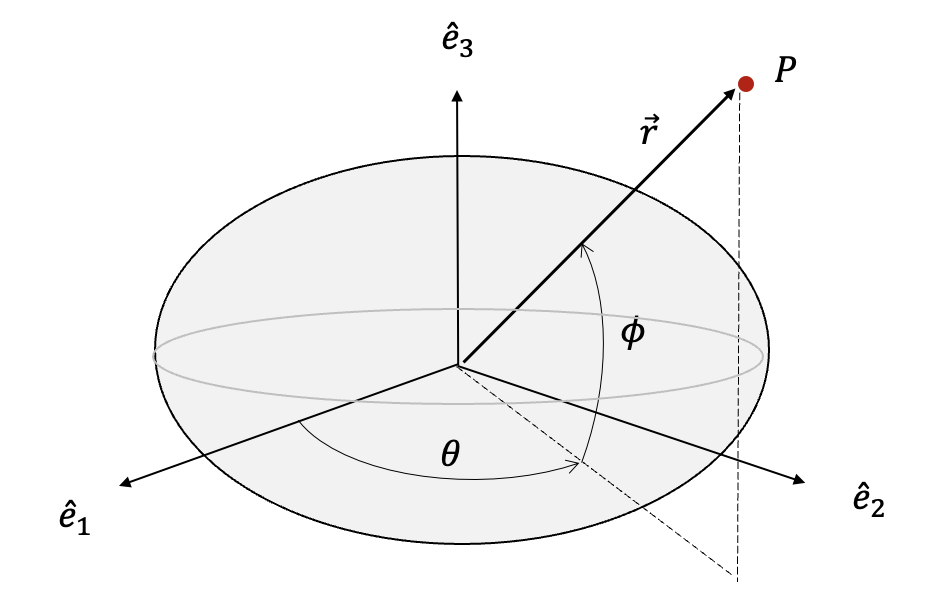
이제 식 (5)를 풀기 위하여 다음과 같이 구좌표계(spherical coordinates)를 도입한다. 여기서 좌표계 \(\{e\}\) 는 천체의 질량 중심을 원점으로 하고 천체에 부착된 좌표계이다.

 

 

그림에서 \(\lambda\) 와 \(\alpha\) 는 각각 미소 질점의 방위각과 고도각, \(\theta\) 와 \(\phi\) 는 각각 위치 \(P\) 의 방위각과 고도각이다. 그러면 미소 질점 \(dm\) 은 다음과 같이 거리, 방위각 및 고도각의 함수로 표현할 수 있다.

 

\[ \begin{align} dm &= D(\rho, \lambda, \alpha) (d\rho)(\rho \cos \alpha d\lambda)(\rho d\alpha) \tag{6} \\ \\ &=D(\rho, \lambda, \alpha) \rho^2 \cos \alpha \ d\rho \ d\lambda \ d\alpha \end{align} \]

 

여기서 \(D(\rho, \lambda, \alpha)\) 는 해당 미소 질점 위치에서의 밀도이다.

 

 

식 (5)에서 \(\gamma\) 도 구좌표계의 각도로 바꿀 필요가 있다. 구면(sphere) 삼각함수의 코사인법칙을 이용하면 다음과 같은 관계식을 얻을 수 있다 (https://pasus.tistory.com/319).

 

\[ \begin{align} \cos \gamma &= \cos (90^0-\phi) \cos (90^0-\alpha) \tag{7} \\ \\ & \ \ \ \ \ \ \ + \sin (90^0-\phi) \sin (90^0-\alpha) \cos (\theta-\lambda) \\ \\ &= \sin \phi \sin \alpha + \cos \phi \cos \alpha \cos (\theta- \lambda) \end{align} \]

 

이제 식 (5)의 적분을 구해야 하는데 이를 위해서는 르장드로 다항식 \(P_k (\cos \gamma )\) 도 계산해야 한다. 이를 위해서 다음과 같이 르장드로 연관 함수(associated Legendre function) \(P_{k,m}\) 을 도입한다. \(P_{k,m}\) 은 다음과 같이 정의된다.

 

\[ \begin{align} P_{k,m} (\nu) = (1-\nu^2 )^{m/2} \frac{d^m P_k (\nu)}{d\nu^m }, \ \ \ 0 \le m \le k \tag{8} \end{align} \]

 

여기서 \(k\) 는 degree, \(m\) 은 order 를 나타낸다. 식 (8)에 의하면 \(m=0\) 일 때 르장드로 연관 함수 \(P_{k,0}\) 는 \(k\) 차(degree) 르장드르 다항식 \(P_k\) 와 동일하다. 참고로 정의에 의해서 2 차(degree)까지의 르장드르 다항식과 르장드로 연관 함수를 구하면 다음과 같다.

 

\[ \begin{align} & P_0 (\nu )=1, \ \ \ P_1 (\nu)= \nu, \ \ \ P_2 (\nu)= \frac{1}{2} (3\nu^2-1) \tag{9} \\ \\ & P_{1,1} (\nu)= \sqrt{1-\nu^2 } \tag{10} \\ \\ & P_{2,1} (\nu)=3 \nu \sqrt{1-\nu^2 }, \ \ \ P_{2,2} (\nu )=3(1-\nu^2 ) \end{align} \]

 

여기서 목표는 \(P_k (\cos \gamma )\) 를 구좌표계의 각도를 변수로 하는 르장드르 다항식과 연관 함수로 표현하는 것이다.

 

\[ \begin{align} P_k (\cos \gamma )=P_k (\sin \phi \sin \alpha + \cos \phi \cos \alpha \cos (\theta-\lambda) ) \tag{11} \end{align} \]

 

이를 위해서 식 (9)의 르장드르 다항식에서 \(\nu= \cos \alpha\) 를 대입해보자.

 

\[ \begin{align} P_1 (\cos \alpha )= \cos \alpha, \ \ \ P_2 (\cos \alpha )= \frac{1}{2} (3 \cos^2 \alpha-1) \tag{12} \end{align} \]

 

식 (10)의 르장드로 연관함수에는 \(\nu=\sin \alpha\) 를 대입해보자.

 

\[ \begin{align} & P_{1,1} (\sin \alpha )= \cos \alpha, \ \ \ P_{2,1} (\sin \alpha )=3 \sin \alpha \cos \alpha \tag{13} \\ \\ & P_{2,2} (\sin \alpha )=3 \cos^2 \alpha \end{align} \]

 

이제 식 (12)와 (13)을 이용하여 식 (11)에서 1 차 르장드로 다항식부터 차례로 계산한다.

 

\[ \begin{align} P_1 (\cos \gamma ) &= \cos \gamma = \sin \phi \sin \alpha+ \cos \phi \cos \alpha \cos (\theta-\lambda) \tag{14} \\ \\ &=P_1 (\sin \phi ) P_1 (\sin \alpha )+P_{1,1} (\sin \phi ) P_{1,1} (\sin \alpha ) \cos (\theta-\lambda) \end{align} \]

 

2 차 르장드로 다항식부터는 상당히 복잡해진다.

 

\[ \begin{align} P_2 (\cos \gamma ) &= \frac{1}{2} (3 \cos^2 \gamma-1) \tag{15} \\ \\ &= \frac{1}{2} (3( \sin \phi \sin \alpha + \cos \phi \cos \alpha \cos (\theta-\lambda) )^2-1) \\ \\ &=P_2 (\sin \phi ) P_2 (\sin \alpha )+\frac{1}{3} P_{2,1} (\sin \phi ) P_{2,1} (\sin \alpha ) \cos (\theta-\lambda) \\ \\ & \ \ \ + \frac{1}{12} P_{2,2} (\sin \phi ) P_{2,2} (\sin \alpha ) \cos 2(\theta-\lambda) \end{align} \]

 

연역법을 이용하여 \(k\) 차 르장드로 다항식을 구하면 다음과 같다.

 

\[ \begin{align} P_k (\cos \gamma ) &=P_k (\sin \phi ) P_k (\sin \alpha ) \tag{16} \\ \\ & \ \ \ +2 \sum_{m=1}^k \frac{(k-m)!}{(k+m)!} P_{k,m} (\sin \phi ) P_{k,m} (\sin \alpha ) \cos m(\theta-\lambda) \end{align} \]

 

이제 식 (16)을 식 (5)에 대입하면 다음과 같다.

 

\[ \begin{align} V(\vec{r} ) &= - \frac{GM}{r}- \sum_{k=1}^\infty \frac{1}{r^{k+1}} A_k P_k (\sin \phi ) \tag{17} \\ \\ & \ \ \ \ \ -\sum_{k=1}^\infty \frac{1}{r^{k+1}} \sum_{m=1}^k P_{k,m} (\sin \phi )(B_{k,m} \cos m\theta+C_{k,m} \sin m\theta ) \end{align} \]

 

여기서

 

\[ \begin{align} & A_k= G \iiint P_k (\sin \alpha ) D(\rho, \lambda, \alpha) \rho^{k+2} \cos \alpha \ d \rho \ d\lambda \ d\alpha \tag{18} \\ \\ & B_{k,m}=2G \frac{(k-m)!}{(k+m)!} \iiint P_{k,m} (\sin \alpha ) \cos m \lambda \ D(\rho, \lambda, \alpha) \rho^{k+2} \cos \alpha \ d\rho \ d\lambda \ d\alpha \\ \\ & C_{k,m}=2G \frac{(k-m)!}{(k+m)!} \iiint P_{k,m} (\sin \alpha ) \sin m\lambda \ D(\rho, \lambda, \alpha) \rho^{k+2} \cos \alpha \ d\rho \ d\lambda \ d \alpha \end{align} \]

 

이다.

 

 

지구를 비롯한 대부분의 태양계 행성은 질량 분포를 자전축을 중심으로 하는 축대칭으로 근사화할 수 있다.

 

 

만약 질량 분포가 \(z(\hat{e}_3)\)-축에 대해서 대칭이라면, 즉 밀도가 \(\rho\) 와 \(\alpha\) 만의 함수로서 \(D(\rho, \lambda, \alpha)=D(\rho, \alpha)\) 이라면, 식 (18)의 \(B_{k,m}\) 과 \(C_{k,m}\) 은 다음과 같이 \(0\) 이 된다.

 

\[ \begin{align} B_{k,m} &= 2G \frac{(k-m)!}{(k+m)!} \iint P_{k,m} (\sin \alpha ) D(\rho, \alpha) \rho^{k+2} \cos \alpha \left( \int_0^{2\pi} \cos m\lambda \ d\lambda \right) \ d\rho \ d\alpha \tag{19} \\ \\ &=0 \\ \\ C_{k,m} &= 2G \frac{(k-m)!}{(k+m)!} \iint P_{k,m} (\sin \alpha ) D(\rho, \alpha) \rho^{k+2} \cos \alpha \left( \int_0^{2\pi} \sin m\lambda \ d\lambda \right) \ d\rho \ d \alpha \\ \\ &=0 \end{align} \]

 

식 (18)의 \(A_k\) 에서 첫번째 항인 \(A_1\) 도 다음과 같이 \(0\) 이 된다.

 

\[ \begin{align} A_1 &= G \iiint P_1 (\sin⁡ \alpha ) D(\rho, \alpha) \rho^3 \cos \alpha \ d\rho \ d\lambda \ d\alpha \tag{20} \\ \\ &=G \iiint \rho \sin \alpha D(\rho, \alpha) \rho^2 \cos \alpha \ d\rho \ d\lambda \ d\alpha \\ \\ &=G \iiint \rho \sin \alpha \ dm \\ \\ &=0 \end{align} \]

 

여기서 \(z\)-축에 대해서 대칭이라는 점과 좌표계의 원점이 질량 중심과 일치한다는 점을 이용하면 위 식은 \(x\)-\(y\) 평면에 대한 질량의 \(1\) 차 모멘트이기 때문에 \(0\) 이 되는 것이다.

식 (19)와 (20)을 식 (17)에 대입하면 식 (17)은 다음과 같이 간략화 된다.

 

\[ \begin{align} V(r, \phi) = - \frac{GM}{r}- \sum_{k=2}^\infty \frac{1}{r^{k+1}} A_k P_k (\sin \phi ) \tag{21} \end{align} \]

 

여기서 합(sum)은 \(k=1\) 이 아닌 \(k=2\) 에서 시작되는 것에 주의해야 한다. 일반적으로 식 (20)에서 \(A_k\) 대신에 \(J_k\) 를 다음과 같이 정의하여 사용한다.

 

\[ \begin{align} J_k=-\frac{A_k}{R_e^k GM} \tag{22} \end{align} \]

 

그러면 식 (21)은 다음과 같이 된다.

 

\[ \begin{align} V(r,ϕ)=-\frac{GM}{r} \left[ 1- \sum_{k=2}^\infty \left( \frac{R_e}{r} \right)^k J_k P_k (\sin \phi ) \right] \tag{23} \end{align} \]

 

여기서 \(J_k\) 를 구역 조화항(zonal harmonics)라고 하며 \(R_e\) 로는 천체의 적도 반지름을 사용한다. 식 (23)은 천체 중심을 기준으로 측정한 위도 \(\phi\) 에 따라 달라지는 중력 포텐셜 함수를 나타낸다.

 

 

하지만 지구를 비롯한 태양계 행성의 질량 분포에 대한 정확한 지식이 없기 때문에 식 (18)을 적분하여 \(J_k\) 의 값을 계산하는 것은 불가능하다. 대신 이 값은 해당 행성 주변의 위성 운동 관측을 통해 추정한다. 지구의 경우 \(J_k\) 값은 다음과 같다.

 

\[ \begin{align} & J_2= 1082.63 \times 10^{-6} \tag{24} \\ \\ & J_3 =-2.52 \times 10^{-6} \\ \\ & J_4=-1.61 \times 10^{-6} \\ \\ & J_5=-0.15 \times 10^{-6} \end{align} \]

 

식 (24)에서 보듯이 다른 항에 비해서 J2 항이 압도적으로 크다. 따라서 보통 중력 섭동에 대한 J2 항의 영향만을 고려하여 J2 항을 제외한 모든 항은 무시하고 식 (23)을 다음과 같이 간략화하여 사용한다.

 

\[ \begin{align} V(r, \phi) &= - \frac{GM}{r} \left[ 1- \left( \frac{R_e}{r} \right)^k J_2 P_2 (\sin \phi ) \right] \tag{25} \\ \\ &= - \frac{GM}{r} \left[ 1-\frac{J_2}{2} \left( \frac{R_e}{r} \right)^2 (3 \sin^2 \phi -1) \right] \end{align} \]

 

식 (17)과 (18)에 의하면 지구의 중력 포텐셜 함수는 기하학적 구조와 질량 분포의 불규칙성으로 인하여 \(\alpha\) 뿐만 아니라 \(\lambda\) 에 따라서도 달라진다. 결과적으로 중력 포텐셜 함수에는 구역 조화항뿐만 아니라 부문 조화항(sectorial harmonics)과 테세리얼 조화항(tesseral harmonics)도 나타난다.

 

 

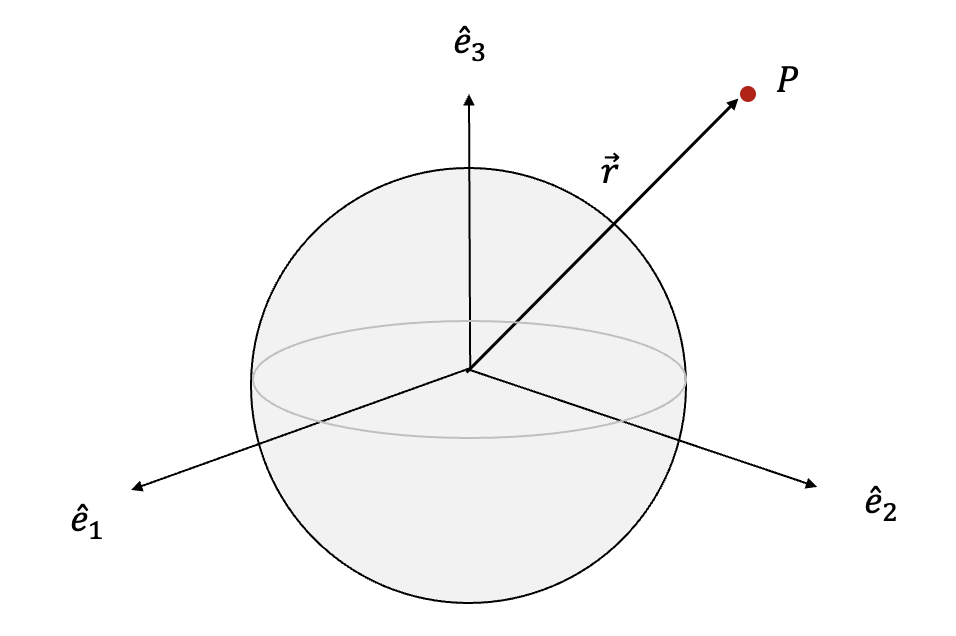
만약 천체가 질량 분포가 구대칭인 구체(sphere)라면, 즉 밀도가 \(\rho\) 만의 함수로서 \(D(\rho, \lambda, \alpha)=D(\rho)\) 이라면, \(B_{k,m}\) 과 \(C_{k,m}\) 은 \(0\) 이 될 뿐만 아니라 \(A_k\) 도 다음과 같이 \(0\) 이 된다. 이 조건에서 \(A_k\) 를 계산하면,

 

\[ \begin{align} A_k=2 \pi G \int_0^R D(\rho) \rho^{k+2} \ d\rho \int_{-\pi/2}^{\pi/2} P_k (\sin \alpha ) \cos \alpha \ d\alpha \tag{26} \end{align} \]

 

이 되는대 여기서 \(\nu= \sin \alpha\) 로 놓으면 \(d\nu=\cos \alpha \ d\alpha\) 이므로,

 

\[ \begin{align} A_k=2\pi G \int_0^R D(\rho) \rho^{k+2} \ d\rho \int_{-1}^1 P_k (\nu) \ d\nu \tag{27} \end{align} \]

 

이 된다. 그런데 여기서 르장드르 다항식의 특성에 의해서 \(k \ne 0\) 일 때 \(\int_{-1}^1 P_k (\nu) \ d\nu =0\) 이므로 \(A_k=0\) 이 된다 (https://pasus.tistory.com/175). 따라서 천체의 질량 분포가 구대칭인 구체(sphere)라면 모든 질량이 구체의 중심에 집중되어 있는 질점과 동일한 중력 포텐셜 함수를 얻을 수 있다.

 

\[ \begin{align} V(r)=-\frac{GM}{r} \tag{28} \end{align} \]