포텐셜 필드 방법
포텐셜 필드(potential field)의 아이디어는 목표점으로 이끄는(attractive) 인공적인 포텐셜 필드와 장애물로부터 멀어지게 내보내는(repulsive) 인공적인 포텐셜 필드를 형상공간에 구축하여, 로봇이나 비행체가 장애물을 피하면서 목표점에 다가갈 수 있는 운행 방향을 찾아보자는 것이다.
인력(attractive) 포텐셜은 로봇이나 비행체를 목표점으로 끄는 목적을 지니고 있으며 보통 파라볼릭(parabolic) 형태와 원추(conical) 형태, 그리고 이 둘을 결합한 형태를 사용하고 있다. 파라볼릭 형태의 포텐셜 필드는 다음 식으로 주어진다.
\[ U_{att1} (\mathbf{q})= \frac{1}{2} k_a \left\vert \mathbf{q}_{goal} - \mathbf{q} \right\vert^2 \]
여기서 \(k_a \gt 0\)은 스케일 파라미터이다. 포텐셜의 경사하강(gradient descent)이 힘(force)이 되므로 인력 포텐셜에 의한 인력(attractive force)는 다음과 같이 목표점까지의 거리의 차이에 비례값으로 주어진다.
\[ \mathbf{f}_{att1} (\mathbf{q})= - \nabla U_{att1} (\mathbf{q})=k_a (\mathbf{q}_{goal}-\mathbf{q}) \]
원추 형태의 포텐셜 필드는 다음 식으로 주어진다.
\[ U_{att2} (\mathbf{q})=k_b \left\vert \mathbf{q}_{goal}- \mathbf{q} \right\vert \]
원추 형태의 인력 포텐셜에 의한 힘은 다음과 같이 목표점까지의 거리에 상관없이 일정한 크기(constant)로 주어진다.
\[ \mathbf{f}_{att2} (\mathbf{q})= - \nabla U_{att2} (\mathbf{q}) = k_a \frac{(\mathbf{q}_{goal}-\mathbf{q})}{\left\vert\mathbf{q}_{goal}-\mathbf{q} \right\vert} \]
목표점과 가까운 거리에서는 \(\mathbf{f}_{att1} (\mathbf{q})\)이 \(\mathbf{f}_{att2} (\mathbf{q})\)보다 작은 크기이기 때문에 오버슈팅(overshooting) 가능성 면에서 바람직하지만 멀리 떨어진 거리에서는 크기가 매우 커지는 단점이 있다. 따라서 먼 거리에서는 원추 형태, 가까운 거리에서는 파라볼릭 형태의 포텐셜 필드를 갖는 결합형을 사용하기도 한다.
\[ U_{att} (\mathbf{q})= \begin{cases} \frac{1}{2} k_a \left\vert \mathbf{q}_{goal} - \mathbf{q} \right\vert^2 , & \mbox{if }\left\vert \mathbf{q}_{goal}- \mathbf{q} \right\vert \le \rho \\ k_b \left\vert \mathbf{q}_{goal}- \mathbf{q} \right\vert , & \mbox{if } \left\vert \mathbf{q}_{goal}- \mathbf{q} \right\vert \gt \rho \end{cases} \]
여기서 \(\left\vert \mathbf{q}_{goal}- \mathbf{q} \right\vert = \rho\) 에서 인력 \(\mathbf{f}_{att} (\mathbf{q})\)의 연속성을 위하여 \(k_b=\rho k_a\)의 조건이 필요하다.
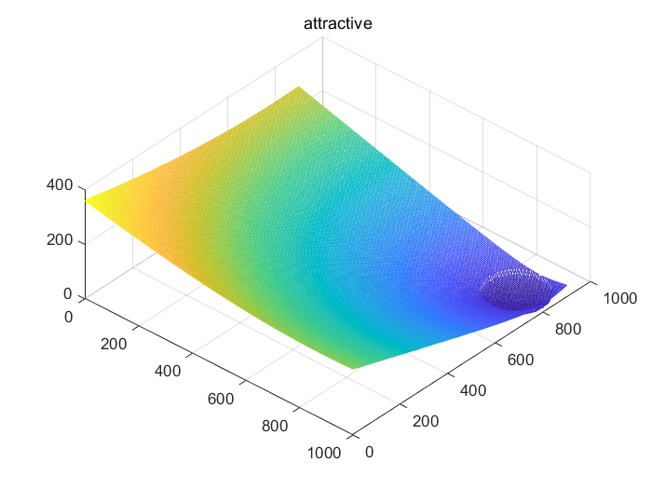
이 때 인력(attractive force)은 다음과 같다.
\[ \mathbf{f}_{att} (\mathbf{q})= -\nabla U_{att} (\mathbf{q}) = \begin{cases} k_a ( \mathbf{q}_{goal} - \mathbf{q} ), & \mbox{if }\left\vert \mathbf{q}_{goal}- \mathbf{q} \right\vert \le \rho \\ k_b \frac{( \mathbf{q}_{goal} - \mathbf{q} )}{\left\vert \mathbf{q}_{goal}- \mathbf{q} \right\vert} , & \mbox{if } \left\vert \mathbf{q}_{goal}- \mathbf{q} \right\vert \gt \rho \end{cases} \]
척력(repulsive) 포텐셜은 로봇이나 비행체를 장애물로부터 떨어지게 밀치는 목적을 지니고 있기 때문에, 장애물 \(i\) 에 대해서 다음과 같은 포텐셜 필드를 갖는다.
\[ U_{rep, i} (\mathbf{q})= \begin{cases} \frac{1}{2} k_{r,i} \left( \frac{1}{d_{min,i} (\mathbf{q}) } - \frac{1}{d^\star_{obs, i}} \right)^2 , & \mbox{if } d_{min, i} \le d^\star_{obs, i} \\ 0 , & \mbox{if } d_{min, i} \gt d^\star_{obs, i} \end{cases} \]
여기서 \(k_{r,i} \gt 0\)이고, \(d_{min, i}= \left\vert \mathbf{q}_{obs,i}-\mathbf{q} \right\vert \)는 장애물 \(i\) 까지의 최단 거리이고 \(d_{obs,i}^\star\)는 미리 설정된 값으로, 만약 로봇이나 비행체가 장애물로부터 일정 거리 \(d_{obs,i}^\star\)이상 떨어져 있으면 장애물에 의한 척력 포텐셜은 무시한다.
척력 포텐셜에 의한 척력(repulsive force)은 다음과 같이 주어진다.
\[ \begin{align} \mathbf{f}_{rep, i} (\mathbf{q}) &= - \nabla U_{rep, i} (\mathbf{q}) \\ \\ &= \begin{cases} \frac{k_{r,i}}{d^2_{min,i}(\mathbf{q}) } \left( \frac{1}{d_{min,i} (\mathbf{q}) } - \frac{1}{d^\star_{obs, i}} \right) \nabla d_{min, i} (\mathbf{q}) , & \mbox{if } d_{min, i} \le d^\star_{obs, i} \\ 0 , & \mbox{if } d_{min, i} \gt d^\star_{obs, i} \end{cases} \end{align} \]
모든 장애물에 의한 척력 포텐셜과 척력은 각 장애물의 척력 포텐셜과 척력의 합으로 주어진다.
\[ \begin{align} & U_{rep} (\mathbf{q}) = \sum_{i=1}^p U_{rep, i} (\mathbf{q}) \\ \\ & \mathbf{f}_{rep} (\mathbf{q}) = \sum_{i=1}^p \mathbf{f}_{rep, i} (\mathbf{q}) \end{align} \]

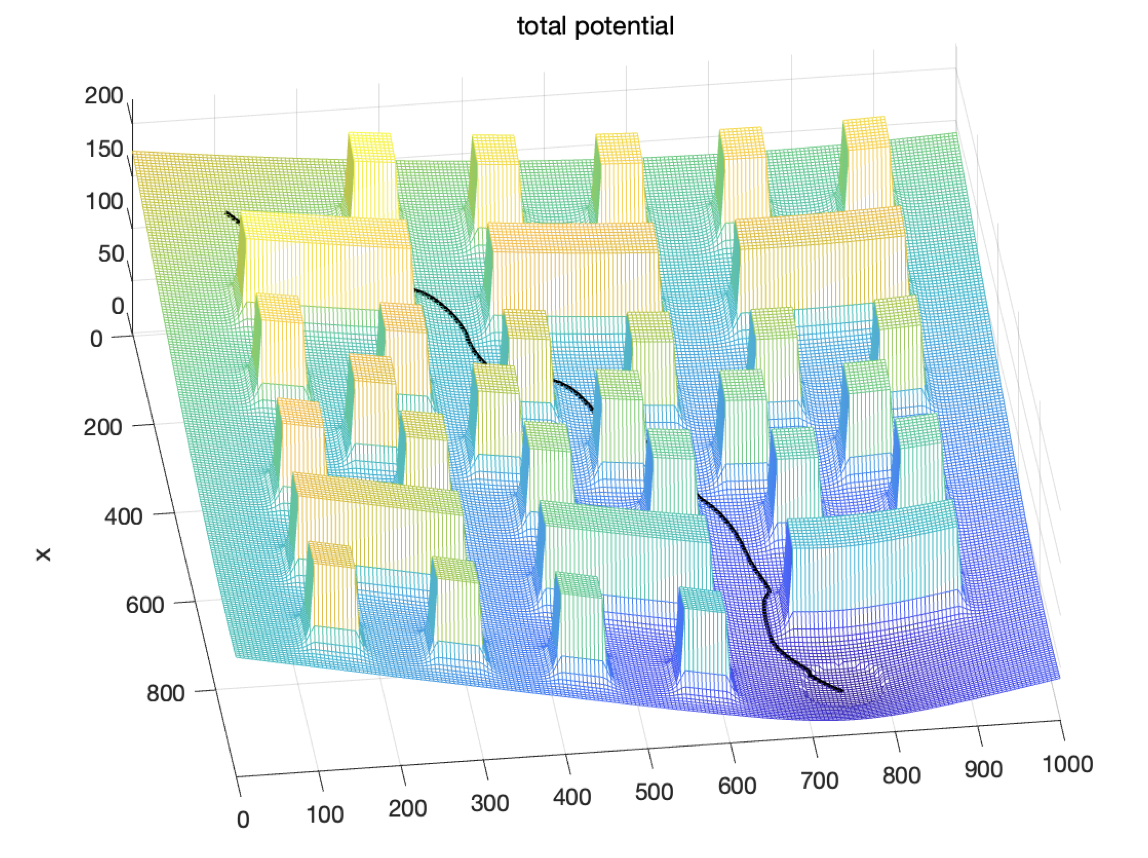
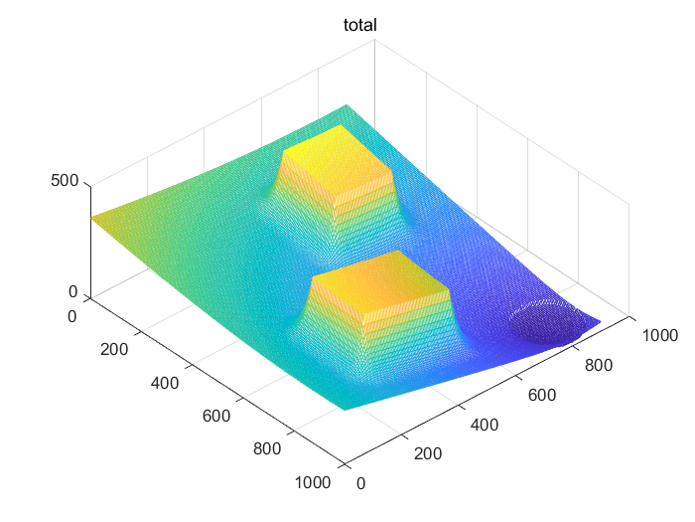
총(total) 포텐셜 필드와 총 힘은 각각 인력 포텐셜과 척력 포텐셜의 합과 인력과 척력의 합으로 주어진다.
\[ \begin{align} & U_{tot} (\mathbf{q}) = U_{att} (\mathbf{q}) + U_{rep} (\mathbf{q}) \\ \\ & \mathbf{f}_{tot} (\mathbf{q}) = \mathbf{f}_{att} (\mathbf{q}) + \mathbf{f}_{rep} (\mathbf{q}) \end{align} \]
경로계획에 포텐셜 필드를 이용할 때는 힘 \(\mathbf{f}_{tot} (\mathbf{q})\)를 로봇이나 비행체에 작용하는 물리적인 힘으로 해석할 수도 있고, 가속도, 또는 속도로 해석하여 적용할 수도 있다.
\(\mathbf{f}_{tot} (\mathbf{q})\)를 힘으로 해석하면 경로가 부드럽게 나오는 반면 속도로 해석하면 경로가 날카롭게 나오는 경향이 있다.
하지만 \(\mathbf{f}_{tot} (\mathbf{q})\)를 힘으로 해석하면 로봇이나 비행체의 동역학 식이 필요하기 때문에, \(\mathbf{f}_{tot} (\mathbf{q})\)를 속도로 해석하는 방법이 많이 쓰인다.
포텐셜 필드의 장점은 임무 환경 전체에 대한 정보가 필요 없고, 로봇이나 비행체의 센서 정보로만으로도 구현 가능하여 온라인(online) 경로계획에 적합하다는 것이다. 단점은 로컬 최소점(local minimum)으로 빠질 수 있다는 것이다. 로컬 최소점 문제를 해결하기 위해 항법식(navigation equation), 하모닉 포텐셜(harmonic potential)식을 이용하는 방법 등이 개발되어 있다.