파티클 군집 최적화 (Particle Swarm Optimization)

파티클 군집 최적화(PSO, particle swarm optimization)는 1995년에 에버하트(Eberhart)와 케네디(Kennedy)가 개발한 최적화 알고리즘으로서 먹이를 찾는 새(bird)들의 군집 행동을 모방해서 개념을 정립했다고 한다. 새 떼는 무리 내부의 리더(leader)나 무리 외부의 통제자 없이 새들간의 상호 작용을 통해 먹이를 찾는다고 한다. 이러한 새들의 집단적 행동을 모방하여 최적화 문제를 풀기 위해서는 군집 지능(swarm intelligence)이라는 전제가 필요하다. 군집 지능은 단순하게 행동하는 개별 에이전트들을 군집으로 적절히 연결하면 그들의 집단적 행동이 매우 지능적인 결과를 만들 수 있다는 것을 의미한다. 즉 멍청한 에이전트들을 연결해 놓으면 전체적으로 똑똑한 행동을 할 수 있다는 뜻이다. (정말?)

 

 

우선 다음과 같이 제약조건이 없는 일반적인 최적화 문제를 보자.

 

\[ \begin{align} \min_{\mathbf{x}} f(\mathbf{x}) \ \ \ \ \ \mbox{or} \ \ \ \ \ \max_{\mathbf{x}}⁡ f(\mathbf{x}) \tag{1} \end{align} \]

 

여기서 \(\mathbf{x} \in \mathbb{R}^n\) 은 최적화 변수이고, \(f(\mathbf{x})\) 는 목적함수(objective function)이다.

위 최적화 문제를 염두에 두고 PSO에서는 어떤 방법으로 새떼가 먹이를 찾는 과정을 최적화 문제로 모델링했는지 살펴보자.

우선 개별적인 새는 파티클로, 새떼는 파티클 군집으로, 먹이를 찾는 과정은 목적함수의 최적값(최소값 또는 최대값)을 구하는 과정으로 해석한다. 최적화 문제에서 파티클은 최적해의 후보군으로 보면 된다. 따라서 파티클은 \(\mathbf{x}_t^{(i)} \in \mathbb{R}^n\) 로 표기한다. 여기서 상첨자 \(i\) 는 \(i\)번째 파티클을, 하첨자 \(t\) 는 시간스텝(time step) 또는 \(t\)번째 이터레이션(iteration)을 나타낸다. 최적화 문제는 이터레이션 방법으로 풀고 매 이터레이션마다 파티클의 위치인 \(\mathbf{x}_t^{(i)}\) 값이 바뀌기 때문에 \(t\) 를 시간스텝과 이터레이션 횟수라는 두 가지 관점에서 볼 수 있다.

새는 개별적으로 움직할 수 있으며 자신의 현재 위치와 지금까지 이동하면서 얻은 먹이와 가장 가까운 위치를 알 수 있다. 즉 파티클은 \(n-\)차원 공간에서 개별적으로 이동할 수 있으며 \(f(\mathbf{x}_t^{(i)}) \) 의 값을 알 수 있고 지금까지 이터레이션 과정에서 얻은 최상의 위치 \(\mathbf{p}_t^{(i) } = \arg\min_{\mathbf{x}_j^{(i) }} f(\mathbf{x}_j^{(i) }), \ \ j=0,...,t\) 를 알 수 있다. 이 정보는 파티클의 개별적인 지식에 해당한다.

군집을 이루는 개별적인 새는 주위 새들과의 상호 작용을 통해 무리 전체에서 지금까지 이동하면서 얻은 먹이와 가장 가까운 위치를 알 수 있다. 즉 파티클은 무리 전체의 최상의 위치 \(\mathbf{p}_t^{global}= \arg\min_{ \mathbf{p}_t^{(i) } } f(\mathbf{p}_t^{(i) }),\ \ i=1,...,N\), 와 \(f(\mathbf{p}_t^{global})\) 의 값을 알 수 있다. 이 정보는 주변의 다른 파티클들을 통해 얻은 군집 지식에 해당한다.

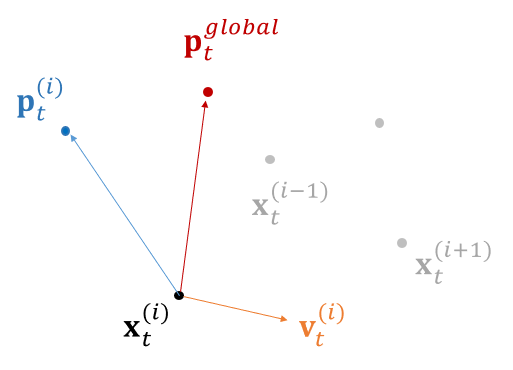
새들은 개별적인 정보와 군집으로 통해 얻은 정보를 이용하여 어느 방향으로 날아갈지를 정한다. 즉 각 파티클은 개별 정보와 군집 정보를 통해 자신의 위치 \(\mathbf{x}_t^{(i) }\) 를 수정한다. 위치의 수정은 속도라는 개념으로 표현할 수 있다.

 

 

PSO 알고리즘에서 파티클 \(i\) 의 위치는 다음 식으로 업데이트된다.

 

\[ \begin{align} \mathbf{x}_{t+1}^{(i) } = \mathbf{x}_t^{(i) }+ \mathbf{v}_{t+1}^{(i) } \Delta t \tag{2} \end{align} \]

 

여기서 \(\Delta t\) 는 시간스텝의 간격이고 \(\mathbf{v}_{t+1}^{(i) } \in \mathbb{R}^n\) 는 시간스텝 \(t+1\) 에서 파티클 \(i\) 의 속도다. 각 파티클은 속도에 따라 움직인다.

PSO 알고리즘에서 파티클 \(i\) 의 속도는 퍼티클이 지금까지 가장 좋은 결과를 얻은 위치를 기억하고, 무리 전체가 지금까지 가장 좋은 결과를 얻은 위치에 대한 정보를 반영하여 다음과 같이 업데이트한다.

 

\[ \begin{align} \mathbf{v}_{t+1}^{(i) } = w \mathbf{v}_t^{(i) }+ c_1 r_1 \frac{1}{\Delta t} (\mathbf{p}_t^{(i) }- \mathbf{x}_t^{(i) } )+ c_2 r_2 \frac{1}{\Delta t} (\mathbf{p}_t^{global}- \mathbf{x}_t^{(i) } ) \tag{3} \end{align} \]

 

여기서 \(\mathbf{p}_t^{(i) }\) 는 파티클 \(i\) 가 처음부터 시간스텝(이터레이션) \(t\) 까지의 과정에서 얻은 로컬 최상의 위치이고, \(\mathbf{p}_t^{global}\) 는 무리 전체가 시간스텝(이터레이션) \(t\) 까지의 과정에서 얻은 글로벌 최상의 위치이다. \(c_1\) 은 상수로서 '인지(cognitive)' 계수, \(c_2\) 도 상수로서 소셜(social) 계수라고 하며. \(r_1\) 과 \(r_2\) 는 \([0, \ 1]\) 사이에서 무작위로 선택되는 랜덤 값이다.

식 (3)에 의하면 속도 업데이트는 3가지 구성요소를 합하여 계산된다. 첫번째 항의 \(w\) 는 관성 가중치(inertia weight)로서 업데이트된 속도가 이전 속도와 얼마나 유사한지를 결정한다. 이 값이 크면 마치 무거운 물체가 움직이는 것처럼 예전 속도 그대로 묵직하게 움직이는 경향이 강하고, 이 값이 작으면 움직임이 가벼워진다.

두번째 항은 파티클 \(i\) 가 시간스텝 \(t\) 까지 찾은 최상의 위치를 목표로 다음 움직임의 방향을 정하는 것을 뜻한다. 이 항이 속도 업데이트에 기여하는 정도는 \(c_1 r_1\) 에 의해서 결정되는데 \(c_1 r_1\) 는 \([0, \ c_1]\) 사이에서 무작위로 선택되는 랜덤 값이다. 즉 기여하는 정도가 무작위로 결정된다.

세번째 항은 시간스텝 \(t\) 까지 무리 전체가 찾은 최상의 위치를 목표로 파티클 \(i\) 의 다음 움직임의 방향을 정하는 것을 뜻한다. 이 항이 속도 업데이트에 기여하는 정도는 \(c_2 r_2\) 에 의해서 결정되는데 \(c_2 r_2\) 는 \([0, \ c_2]\) 사이에서 무작위로 선택되는 랜덤 값이다. 마찬가지로 기여하는 정도가 무작위로 결정된다. \(c_1 r_1\) 와 \(c_2 r_2\) 의 상대적인 값은 각각 로컬 탐색과 글로벌 탐색에 비중을 나타낸다고 볼 수 있으며 그 비중은 무작위로 결정된다.

 

 

PSO 알고리즘에서 이터레이션 마다 각 파티클의 위치가 업데이트되는데 이 때 파티클이 미리 설정해 둔 경계를 넘어가는 것을 방지해야 할 필요가 있다. 또한 이터레이션 과정을 종료하기 위한 기준이 필요한데 일반적으로 두 가지 유형이 사용된다. 첫번째는 미리 정의된 이터레이션 횟수에 도달하면 중지시키는 것으로서 매우 간단하며 널리 사용되는 방식이다. 두번째는 수렴 기준을 정해서 조건을 만족하면 실행을 종료하는 것이다. 수렴 조건의 예로는 모든 파티클 사이의 거리가 일정 값 미만으로 수렴하는 것을 들 수 있겠다.

시간스텝의 간격인 \(\Delta t\) 는 인위적인 설정에 불과하기 때문에 문헌에 따라서는 \(\Delta t=1\) 로 놓기도 하고 또는 \(\Delta \mathbf{x}_t^{(i) }= \mathbf{v}_t^{(i) } \Delta t\) 로 놓기도 한다. \(\Delta \mathbf{x}_t^{(i) }= \mathbf{v}_t^{(i) } \Delta t\) 로 논다면 식 (2)와 (3)을 다음과 같이 수정하면 된다.

 

\[ \begin{align} & \mathbf{x}_{t+1}^{(i) } = \mathbf{x}_t^{(i) }+ \Delta \mathbf{x}_{t+1}^{(i) } \tag{4} \\ \\ & \Delta \mathbf{x}_{t+1}^{(i) } = w \Delta \mathbf{x}_t^{(i) }+ c_1 r_1 (\mathbf{p}_t^{(i) }- \mathbf{x}_t^{(i) } )+ c_2 r_2 (\mathbf{p}_t^{global}- \mathbf{x}_t^{(i) } ) \end{align} \]

 

PSO 알고리즘을 정리하면 다음과 같다.

1. \(N \) 개의 파티클에 대해서 위치 \(\mathbf{x}_0^{(i) }\), 속도 \(\mathbf{v}_0^{(i) }\) 을 설정된 경계안에서 초기화 한다.

2. \(N\) 개의 파티클에 대해서 \(\mathbf{p}_0^{(i) }\) 과 \(\mathbf{p}_0^{global}\) 을 초기화 한다.
           \( \mathbf{p}_0^{(i) }= \mathbf{x}_0^{(i) }, \ \ \ \ \ \mathbf{p}_0^{global}= \mathbf{x}_0^{(1) }\)

3. 종료 조건에 도달할 때까지 다음을 반복한다.

   (1) 속도를 업데이트 한다.
           \( \mathbf{v}_{t+1}^{(i) }=w \mathbf{v}_t^{(i) }+c_1 r_1 (\mathbf{p}_t^{(i) }-\mathbf{x}_t^{(i) } )+c_2 r_2 (\mathbf{p}_t^{global}-\mathbf{x}_t^{(i) } ) \)

    (2) 위치를 업데이트 한다.
           \( \mathbf{x}_{t+1}^{(i) }= \mathbf{x}_t^{(i) }+ \mathbf{v}_{t+1}^{(i) } \)

    (3) 파티클의 로컬 최상의 위치 \(\mathbf{p}_{t+1}^{(i) }\) 을 계산한다.

    (4) 무리 전체의 글로벌 최상의 위치 \(\mathbf{p}_{t+1}^{global}\) 을 계산한다.

PSO는 알고리즘의 구현이 간단하고 설계 매개변수가 적다는 장점이 있어서 함수 최적화, 인공 신경망 학습, 퍼지 제어, 패턴 분류 등 많은 문제에 성공적으로 적용되어 왔다. PSO에는 세개의 설계 파라미터(관성 가중치, 인지 계수, 소셜 계수)가 있는데 이 파라미터는 PSO 성능에 큰 영향을 미치며, 이러한 파라미터를 적절히 설정해야 최상의 성능을 얻을 수 있다. 문헌에 의하면 다양한 메커니즘을 통해 이러한 파라미터를 조정하여 PSO의 성능을 향상시키기 위한 연구가 수행되었고 많은 변형된 알고리즘이 존재한다.

PSO는 원래 연속 최적화 문제를 해결하기 위해서 개발되었는데, 최근에는 조합 최적화 문제와 이산 변수 및 연속 변수를 모두 갖는 혼합 정수 비선형 최적화 문제(MINLP)까지 처리할 수 있도록 확장되었다.

다음은 아래와 같은 최적화 문제를 PSO로 풀기 위한 예제다.

 

\[ \begin{align} & \mathbf{x}^* = \arg \min_{\mathbf{x}} ⁡f (\mathbf{x}) \\ \\ & f(\mathbf{x})=(x_1-1)^2+(x_2-2)^2+(x_3+3)^2, \ \ \ \ \ \mathbf{x}=[x_1 \ \ x_2 \ \ x_3 ]^T \end{align} \]

 

답이 \(\mathbf{x}^*=[1 \ \ 2 \ \ -3]^T\) 로 정해져 있으니 PSO 결과와 비교하면 좋을 것이다. 파티클 갯수 50개, 이터레이션 횟수 30회, 관성 가중치 \(w=0.5\), 두 계수를 \(c_1=c_2=1\) 로 했을 때 실행 결과는 다음과 같다.

 

>> pso
iteration 1 : cost = 8.25605 
iteration 2 : cost = 1.41808 
iteration 3 : cost = 0.74344 
iteration 4 : cost = 0.20110 
iteration 5 : cost = 0.17040 
iteration 6 : cost = 0.03820 
iteration 7 : cost = 0.03820 
iteration 8 : cost = 0.03820 
iteration 9 : cost = 0.02189 
iteration 10 : cost = 0.00764 
iteration 11 : cost = 0.00016 
iteration 12 : cost = 0.00016 
iteration 13 : cost = 0.00016 
iteration 14 : cost = 0.00016 
iteration 15 : cost = 0.00005 
iteration 16 : cost = 0.00005 
iteration 17 : cost = 0.00005 
iteration 18 : cost = 0.00003 
iteration 19 : cost = 0.00000 
iteration 20 : cost = 0.00000 
iteration 21 : cost = 0.00000 
iteration 22 : cost = 0.00000 
iteration 23 : cost = 0.00000 
iteration 24 : cost = 0.00000 
iteration 25 : cost = 0.00000 
iteration 26 : cost = 0.00000 
iteration 27 : cost = 0.00000 
iteration 28 : cost = 0.00000 
iteration 29 : cost = 0.00000 
iteration 30 : cost = 0.00000 
optimal position: 0.99999, 1.99997, -3.00003 
optimal value: 0.00000

 

 

 

매트랩 코드는 다음과 같다.

 

% PSO
%
% (c) st.watermelon

clear all

% setup
bounds =[-10 -10 -10;
          10  10  10];

n_particles = 50;
max_iter = 30;

w = 0.5; % inertia
c1 = 1; % coefficients 
c2 = 1;

% initialize
particles = rand(n_particles,3);
for jj = 1:3
    particles(:,jj) = particles(:,jj)*(bounds(2,jj)-bounds(1,jj))+bounds(1,jj);
end
velocities = zeros(n_particles, 3);

personal_best_positions = particles;
personal_best_costs = objective(personal_best_positions);

global_best_position = particles(1,:);
global_best_cost = personal_best_costs(1);

% iteration
for iter = 1:max_iter
    r1 = rand(n_particles, 1);
    r2 = rand(n_particles, 1);

    cognitive_comp = c1.*r1.*(personal_best_positions - particles);
    social_comp = c2.*r2.*(global_best_position - particles);

    velocities = w*velocities + cognitive_comp + social_comp;

    particles = particles + velocities;
    particles = clip(particles, bounds(1,:), bounds(2,:));

    % update minimum position of each particle 
    costs = objective(particles);
    is_best = costs < personal_best_costs;
    personal_best_costs(is_best) = costs(is_best);
    personal_best_positions(is_best, :) = particles(is_best, :);

    % update global minimum position
    [global_best_cost, idx] = min(personal_best_costs);
    global_best_position = personal_best_positions(idx, :);

    fprintf('iteration %d : cost = %.5f \n', iter, global_best_cost);

end

fprintf('optimal position: %.5f, %.5f, %.5f \n', global_best_position);
fprintf('optimal value: %.5f \n', global_best_cost);

%%
function out = objective(pos)

out = (pos(:,1)-1).^2 + (pos(:,2)-2).^2 + (pos(:,3)+3).^2;