대기 항력에 의한 궤도요소의 시간 변화율

고도 100 km 이하의 궤도인 초저궤도(VLEO, Very Low Earth Orbit)가 최근의 우주임무와 관련하여 주목을 받고 있다. 그러나 이러한 낮은 고도를 효율적으로 사용하려면 대기 항력을 극복해야 하는 큰 과제가 있다. 이 문제를 해결하기 위한 한가지 대안으로서 공기 호흡식 플라즈마 추진기(air-breathing plasma thruster) 관련 연구가 활발해지고 있다.

공기 호흡식 플라즈마 추진기는 홀 추진기, 이온 추진기, 자기플라즈마 역학(MPD) 추진기와 같은 기존의 전기추진시스템(electric propulsion system)과는 달리 대기에서 플라즈마를 생성하고 전기와 자기력을 사용하여 추진력을 생성하므로 무거운 탱크가 필요하지 않는 장점이 있다.

여기서는 추력기가 아니라 대기 항력이 궤도에 미치는 영향에 대해서 알아보고자 한다.

지구의 경우 일반적으로 우주가 시작되는 고도를 100 km로 본다. 지구 대기의 99.9999 % 이상을 포함하고 있는 고도이지만, 그럼에도 불구하고 100 km 이상의 고도에서도 희박한 대기이지만 우주비행체에 항력을 발생시킨다. 항력의 주된 효과는 궤도의 크기를 축소하는 것이며, 많은 경우 인공위성이 대기권에 재진입하여 지구에 추락하는 원인이 된다.

국제우주정거장은 약 400 km 상공에서 거의 원형에 가까운 궤도를 돌도 있지만 이 고도에서도 항력의 영향을 상쇄하려면 추진 기동이 필요하다. 보통 우주정거장을 방문하는 우주비행체의 추진 시스템으로 부스팅을 한다고 한다.

허블 우주 망원경도 고도 560 km의 원형 궤도를 돌고 있지만 역시 항력으로 인해 궤도를 유지하기 위한 추진 기동이 필요하다. 1993년부터 2009년까지는 우주왕복선이 허블 망원경을 다섯 차례 방문하여 망원경을 정비하고 부스팅을 했다고 한다. 허블 망원경은 자체 추진 시스템이 없는 관계로 2025년경에는 궤도를 이탈할 것으로 예상되고 있다.

대기 항력은 우주비행체의 운동 방향과 반대로 작용한다. 대기 항력에 의한 가속도는 다음과 같이 주어진다.

 

\[ \begin{align} \vec{a}_D &=- C_D \frac{1}{2} \rho v_{rel}^2 \frac{A}{m} \frac{\vec{v}_{rel}}{v_{rel}} \tag{1} \\ \\ &= - \frac{1}{2 \beta} \rho v_{rel}^2 \frac{\vec{v}_{rel}}{v_{rel}} \end{align} \]

 

여기서 \(A\) 는 우주비행체의 정면 면적(상대 속도 벡터에 수직인 면적), \(C_D\) 는 항력계수, \(\vec{v}_{rel}\) 는 대기에 대한 우주비행체의 상대 속도벡터, \(\beta= \frac{m}{C_D A}\) 는 탄도계수 (ballistic coefficient)이다.

 

 

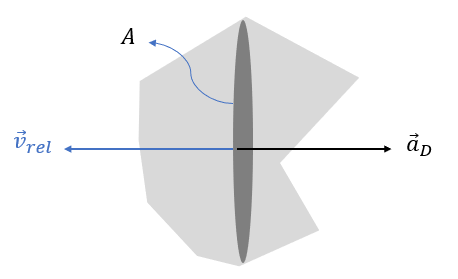
상대 속도벡터는 다음과 같다.

 

\[ \begin{align} \vec{v}_{rel}= \vec{v} -\vec{v}_{atm} \tag{2} \end{align} \]

 

여기서 \(\vec{v}\) 와 \(\vec{v}_{atm}\) 는 각각 관성좌표계에 대한 우주비행체의 속도와 대기 속도이다. 만약 대기가 지구와 함께 회전한다면 대기 속도는 다음과 같다.

 

\[ \begin{align} \vec{v}_{atm} = ^i \vec{\omega}^e \times \vec{r} \tag{3} \end{align} \]

 

여기서 \(^i \vec{\omega}^e\) 는 지구 자전 각속도 벡터, \(\vec{r}\) 은 지구 중심에서 우주비행체까지의 거리 벡터이다.

항력을 정확하게 결정하는 데 있어 어려운 부분은 정확한 대기 밀도와 우주비행체의 자세를 구하는 것이다. 우주비행체는 자세에 따라 항력의 영향을 다양하게 받는다. 정면 단면적은 궤도에서 작동 중인 인공위성의 경우 잘 알려져 있지만, 재진입에 가까워지면 위성이 텀블링을 시작하고 자세가 변하므로 면적이 급격히 변할 수 있다.

 

 

대기 항력에 의한 궤도요소(orbital elements)의 시간 변화율은 가우스 행성 방정식(Gauss planetary equation)을 이용하여 계산할 수 있다. 하지만 가우스 행성 방정식에 있는 섭동 가속도는 LVLH(local-vertical-local-horizontal) 좌표계 \(\{o\}\) 의 축성분으로 표현되어 있으므로 식 (1)로 주어진 대기 항력에 의한 섭동 가속도를 좌표계 \(\{o\}\) 로 변환해야 한다.

 

 

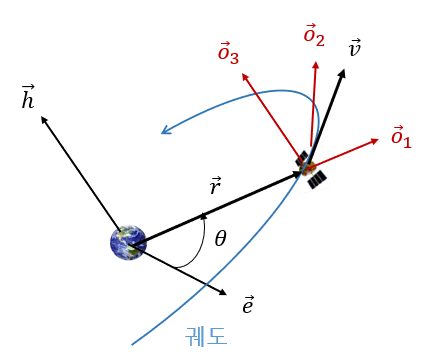
논의를 단순하게 하기 위해서 대기의 회전을 무시한다면 식 (1)의 섭동 가속도는 다음과 같이 된다.

 

\[ \begin{align} \vec{a}_D=- \frac{1}{2 \beta} \rho v^2 \frac{\vec{v}}{v} \tag{4} \end{align} \]

 

게시글 (https://pasus.tistory.com/288)에 의하면 속도벡터의 방향 성분을 LVLH 좌표계로 표현하면 다음과 같다.

 

\[ \begin{align} & \frac{\vec{v}}{v} \cdot \hat{o}_1 = \frac{1}{v} \sqrt{\frac{\mu}{p} } e \sin \theta = \frac{\mu}{vh} e \sin \theta \tag{5} \\ \\ & \frac{\vec{v}}{v} \cdot \hat{o}_2 = \frac{1}{v} \sqrt{\frac{\mu}{p} } (1+e \cos \theta )= \frac{h}{vp} (1+e \cos \theta )= \frac{h}{vr} \\ \\ & \frac{\vec{v}}{v} \cdot \hat{o}_3=0 \end{align} \]

 

식 (5)를 이용하면 식 (4)의 섭동 가속도는 다음과 같이 LVLH 좌표계의 축성분으로 표현할 수 있다.

 

\[ \begin{align} & a_r= \vec{a}_D \cdot \hat{o}_1=- \frac{1}{2 \beta} \rho v \frac{\mu}{h} e \sin \theta \tag{6} \\ \\ & a_\theta= \vec{a}_D \cdot \hat{o}_2=- \frac{1}{2 \beta} \rho v \frac{h}{r} \\ \\ & a_h= \vec{a}_D \cdot \hat{o}_3=0 \end{align} \]

 

식 (6)을 게시글 (https://pasus.tistory.com/346)에 있는 가우스 행성 방정식에 대입하면 대기 항력에 의한 궤도요소의 시간 변화율을 다음과 같이 구할 수 있다.

 

\[ \begin{align} \frac{da}{dt} &= \frac{2a^2}{h} e \sin \theta \ a_r+ \frac{2a^2}{h} (1+e \cos \theta ) \ a_\theta \tag{7} \\ \\ & =-\frac{a^2}{h} e \sin \theta \left( \frac{1}{\beta} \rho v \frac{\mu}{h} e \sin \theta \right)-\frac{a^2}{\beta}(1+e \cos \theta ) \left( \frac{\rho v}{r} \right) \\ \\ &=-\frac{\rho v a^2}{\beta} \left[ \frac{\mu}{h^2} e^2 \sin^2⁡ \theta + \frac{\mu}{h^2} (1+e \cos \theta )^2 \right] \\ \\ &=-\frac{\rho v^3 a^2 }{\beta \mu} \\ \\ \\ \frac{de}{dt}&= \frac{h}{\mu} \sin \theta \ a_r+ \frac{1}{h} \left[ \left( r+ \frac{h^2}{\mu} \right) \cos \theta +er \right] \ a_\theta \\ \\ &=-\frac{\rho v}{2 \beta} \left[ e \sin^2 ⁡\theta +(2+e \cos \theta ) \cos \theta+e \right] \\ \\ & =-\frac{\rho v}{\beta} (e+\cos \theta ) \\ \\ \\ \frac{di}{dt}&= \frac{r}{h} \cos (\omega + \theta) \ a_h = 0 \\ \\ \\ \frac{d\Omega}{dt} &= \frac{r \sin (\omega + \theta) }{h \sin i } \ a_h = 0 \\ \\ \\ \frac{d \omega }{dt} &= - \frac{h}{e \mu } \cos \theta \ a_r + \frac{1}{eh} \left( r+ \frac{h^2}{\mu} \right) \sin \theta \ a_\theta - \frac{r \sin (\omega + \theta ) }{h \tan i } \ a_h \\ \\ &= \cos \theta \frac{1}{2 \beta} \rho v \sin \theta - \frac{1}{e} \left( 1+ \frac{h^2}{\mu r} \right) \sin \theta \frac{1}{2 \beta } \rho v \\ \\ & = - \frac{\rho v}{e \beta} \sin \theta \\ \\ \\ \frac{d\theta}{dt} &= \frac{h}{r^2} + \frac{h}{e \mu} \cos \theta \ a_r- \frac{1}{eh} \left(r+ \frac{h^2}{\mu} \right) \sin \theta \ a_\theta \\ \\ &= \frac{h}{r^2} + \frac{\rho v}{2e \beta} [-e \cos \theta \sin \theta+ \sin \theta (2+e \cos \theta )] \\ \\ &= \frac{h}{r^2} + \frac{\rho v}{e \beta} \sin \theta \\ \\ \\ \frac{dh}{dt} & =r \ a_\theta \\ \\ & =-\frac{1}{2 \beta} \rho v h \end{align} \]

 

여기서

 

\[ \begin{align} & \vec{v}= \frac{\mu}{h} e \sin \theta \hat{o}_1+ \frac{\mu}{h} (1+e \cos \theta ) \hat{o}_2 \tag{8} \\ \\ & r= \frac{p}{1+e \cos \theta }, \ \ \ \ \ \ p=\frac{h^2}{\mu} \end{align} \]

 

를 이용하였다.

식 (7)에 의하면 항력으로 인해 반장축이 단조 감소한다는 것을 알 수 있다. 이 결과는 항력으로 인해 우주비행체가 에너지를 잃는다는 사실을 뒷받침한다. 마찬가지로 항력으로 인해 이심률도 평균적으로 감소하여 점점 원형 궤도가 된다. 또한 궤도 경사각과 RAAN은 대기 항력의 영향을 받지 않는다는 것을 알 수 있다.