[seq2seq] 어텐션이 포함된 seq2seq 모델
Sequence-to-sequence (seq2seq) 모델에서 인코더(encoder)는 입력 시퀀스를 고정된 길이를 갖는 컨텍스트 벡터로 압축하고, 디코더(decoder)는 이를 사용하여 전체 출력 시퀀스를 생성한다. 컨텍스트 벡터는 인코더의 맨 마지막 시퀀스 스텝(시간스텝)에서 생성되며, 인코더와 디코더를 연결하는 유일한 통로이자 인코더가 입력 시퀀스에서 취득한 모든 정보가 흐르는 길목이다.

기존 seq2seq 모델은 인코더와 디코더가 컨텍스트 벡터로만 연결되기 때문에 두가지 문제가 발생한다.
첫번째 문제는 고정된 길이를 갖는 1개의 컨텍스트 벡터만으로는 디코더로 전달하는 정보의 양이 제한되거나 소실된다는 점이다. 이를 병목(bottleneck) 현상이라고 하는데 입력 시퀀스가 매우 길어서 인코더가 처리해야 하는 정보의 양이 많을 수록 더 문제가 된다. 그렇다고 컨텍스트 벡터의 길이를 확장하기 위해 은닉상태(hidden state) 수를 늘리면 짧은 시퀀스에 대해서 모델이 과적합 될 수 있거나 성능이 저하될 수 있다.

일례로 앞서 살펴본 5자리의 입력 숫자열을 반대 순서로 정렬된 숫자열로 변환하여 출력시키는 seq2seq 예제 (https://pasus.tistory.com/290)에서 입력 숫자열 길이를 10으로 두 배 늘리면 학습 능력이 대폭 하락하는 것을 볼 수 있다.
Epoch 45/50
125/125 - 2s - loss: 0.5716 - accuracy: 0.7951 - val_loss: 0.5486 - val_accuracy: 0.8065 - 2s/epoch - 13ms/step
Epoch 46/50
125/125 - 2s - loss: 0.5458 - accuracy: 0.8064 - val_loss: 0.5320 - val_accuracy: 0.8178 - 2s/epoch - 13ms/step
Epoch 47/50
125/125 - 2s - loss: 0.5370 - accuracy: 0.8120 - val_loss: 0.5382 - val_accuracy: 0.8146 - 2s/epoch - 13ms/step
Epoch 48/50
125/125 - 2s - loss: 0.5344 - accuracy: 0.8125 - val_loss: 0.5433 - val_accuracy: 0.8104 - 2s/epoch - 13ms/step
Epoch 49/50
125/125 - 2s - loss: 0.5437 - accuracy: 0.8073 - val_loss: 0.5146 - val_accuracy: 0.8247 - 2s/epoch - 13ms/step
Epoch 50/50
125/125 - 2s - loss: 0.5246 - accuracy: 0.8150 - val_loss: 0.5532 - val_accuracy: 0.8067 - 2s/epoch - 13ms/step

다음은 임의로 생성된 10개의 시퀀스 데이터에 대해서 테스트한 결과다. 출력 시퀀스의 정확도가 겨우 20%로서 정확도가 매우 떨어진 것을 볼 수 있다.
Input Exact Predicted T/F
[5, 1, 0, 6, 2, 2, 9, 6, 4, 4] [4, 4, 6, 9, 2, 2, 6, 0, 1, 5] [4, 6, 4, 7, 2, 9, 1, 4, 0, 0] False
[6, 8, 4, 5, 8, 8, 7, 0, 7, 7] [7, 7, 0, 7, 8, 8, 5, 4, 8, 6] [7, 7, 0, 7, 8, 8, 5, 4, 8, 6] True
[3, 5, 4, 5, 6, 3, 7, 4, 1, 2] [2, 1, 4, 7, 3, 6, 5, 4, 5, 3] [2, 1, 4, 7, 3, 5, 6, 4, 6, 1] False
[8, 2, 8, 0, 3, 4, 2, 2, 7, 4] [4, 7, 2, 2, 4, 3, 0, 8, 2, 8] [4, 7, 2, 2, 4, 3, 8, 2, 0, 7] False
[8, 9, 9, 0, 2, 6, 0, 4, 0, 2] [2, 0, 4, 0, 6, 2, 0, 9, 9, 8] [0, 2, 2, 4, 0, 6, 1, 9, 6, 4] False
[0, 4, 6, 8, 5, 1, 5, 1, 8, 4] [4, 8, 1, 5, 1, 5, 8, 6, 4, 0] [4, 8, 1, 5, 1, 8, 5, 7, 4, 9] False
[5, 0, 9, 4, 7, 1, 9, 7, 1, 7] [7, 1, 7, 9, 1, 7, 4, 9, 0, 5] [7, 1, 7, 9, 1, 7, 4, 9, 5, 0] False
[0, 1, 0, 2, 1, 1, 5, 8, 0, 1] [1, 0, 8, 5, 1, 1, 2, 0, 1, 0] [1, 8, 0, 9, 3, 1, 0, 3, 6, 2] False
[9, 5, 1, 2, 0, 6, 5, 7, 0, 1] [1, 0, 7, 5, 6, 0, 2, 1, 5, 9] [1, 0, 7, 5, 6, 0, 2, 1, 5, 9] True
[0, 9, 8, 7, 7, 3, 8, 0, 8, 6] [6, 8, 0, 8, 3, 7, 7, 8, 9, 0] [8, 6, 2, 3, 6, 4, 8, 8, 4, 5] False
Accuracy: 0.2
둘째는 입력 시퀀스가 매우 길 경우 LSTM을 사용함에도 불구하고 그래디언트 소실(gradient vanishing)문제가 여전히 발생한다는 것이다.
기존 seq2seq 문제를 해결하기 위한 아이디어로는 인코더와 디코더를 연결하는 통로의 갯수를 늘리는 것을 들 수 있을 것이다. 즉, 디코더로 연결되는 통로를 인코더의 맨 마지막 스텝에서 뿐만 아니라 인코더의 모든 시간스텝(time step)으로 확대하는 것이다.

하지만 LSTM의 메모리셀(memory cell)에 은닉상태(hidden state)와 셀상태(cell state)외에 추가적인 연결고리를 만드는 것은 쉽지 않은 일이다.

대신에 디코더의 매 시간스텝마다 출력 시퀀스를 생성하는 데 필요한 정보를 인코더의 모든 시간스텝에서 찾아볼 수 있게 하면 어떨까. 이러한 아이디어를 구현한 것이 어텐션(attention) 메카니즘이다. 이름 그대로 인코더의 모든 시간스텝을 찾아보되 해당 디코딩 단계에서 연관성이 큰 인코딩 정보에 집중하는 메카니즘이다.
어텐션 메카니즘을 개략적으로 설명하면 다음과 같다. 우선 인코더에서는 매 시간스텝마다 디코더가 필요로 할 수 있는 정보를 키-밸류 (key-value) 형태로 만들어 둔다.

디코더는 특정 시간스텝에서 필요한 정보를 인코더가 가지고 있는지 여부를 인코더의 각 스텝에 질의(query)한다.

그러면 어텐션 매커니즘은 디코더의 질의(query)에 대해 인코더의 키(key)를 모두 비교하여 유사한 정도를 점수(score)로 계산한다.
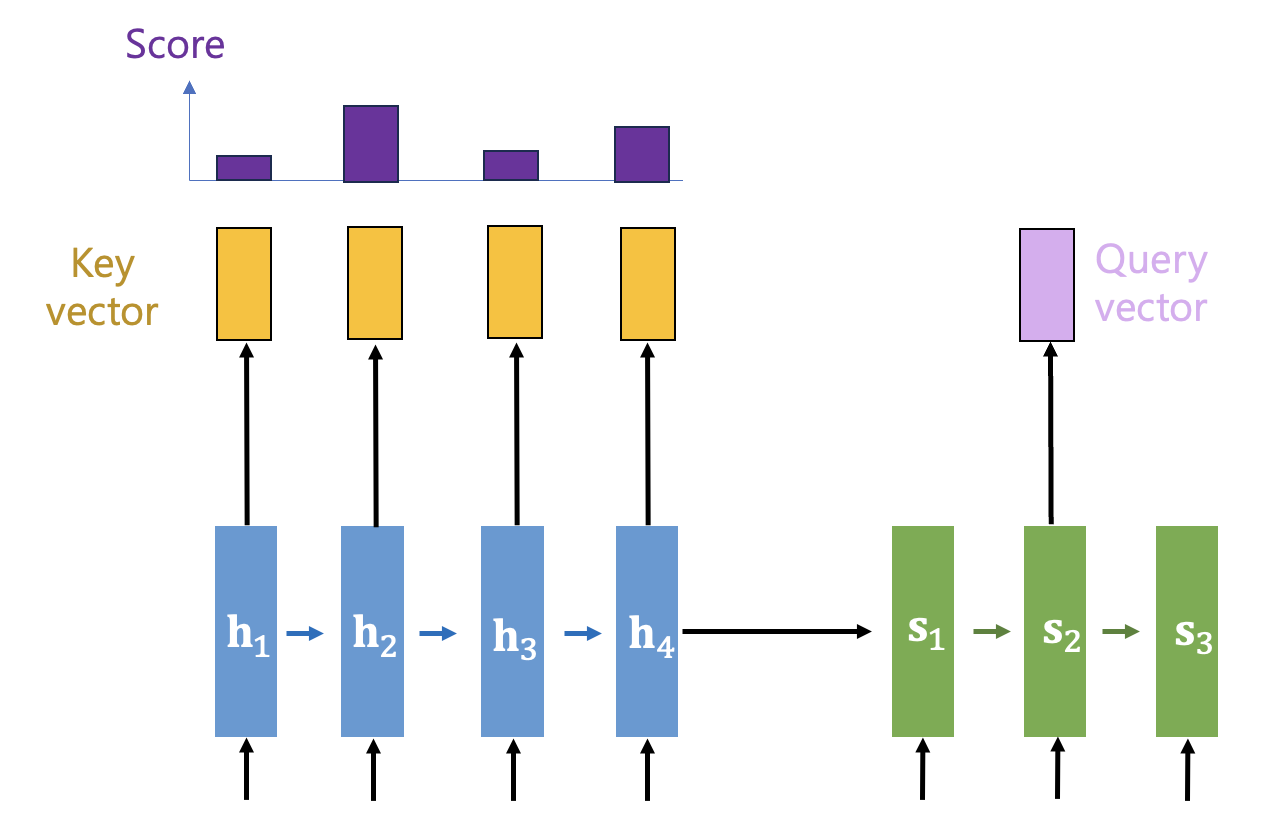
점수가 높을 수록 질의와 관련성이 높다고 간주하고 해당 키(key)와 매칭된 정보(밸류, value)와 점수분포(score distribution)의 가중합을 계산하여 컨텍스트 벡터를 만든다. 그리고 디코더의 질의(query)한 곳으로 전달한다.
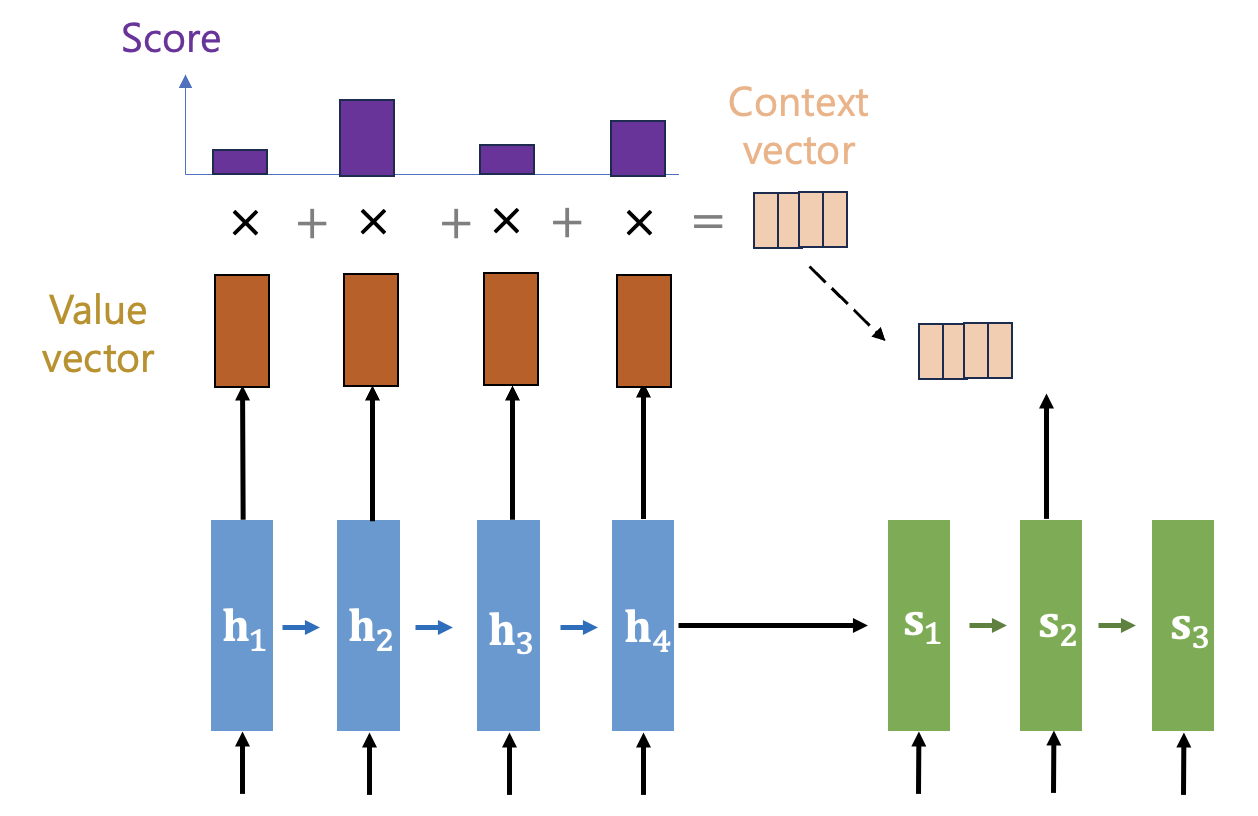
러면 디코더에서는 질의(query)한 해당 스텝에서의 은닉상태와 컨텍스트 벡터를 결합(concatenation)하여 출력을 계산한다.
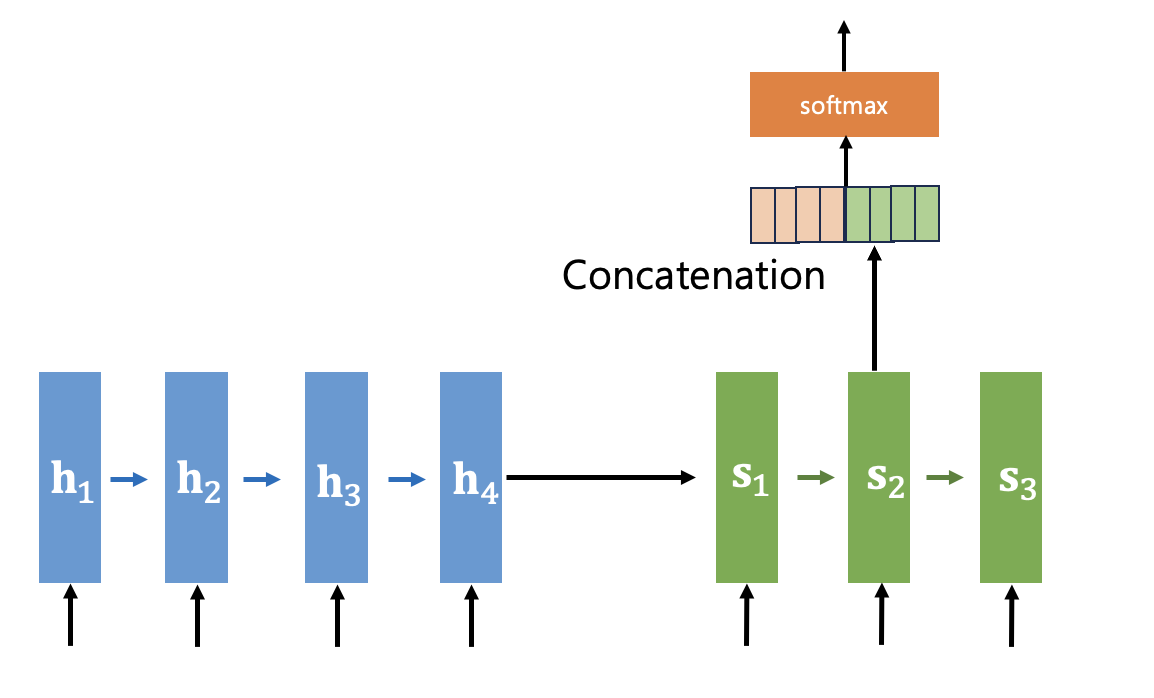
또는 다음 시간스텝의 디코더 입력과 결합하는 방식을 사용하기도 한다.
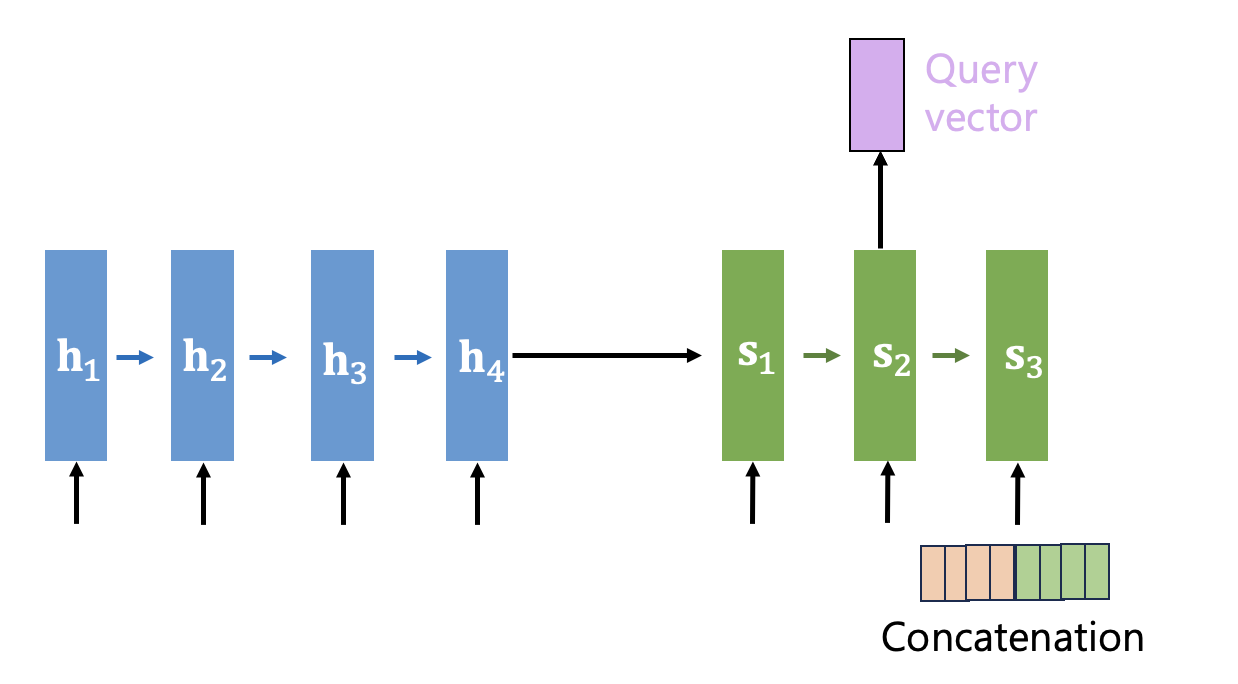
이제 어텐션 메커니즘을 단계별로 자세히 설명한다.
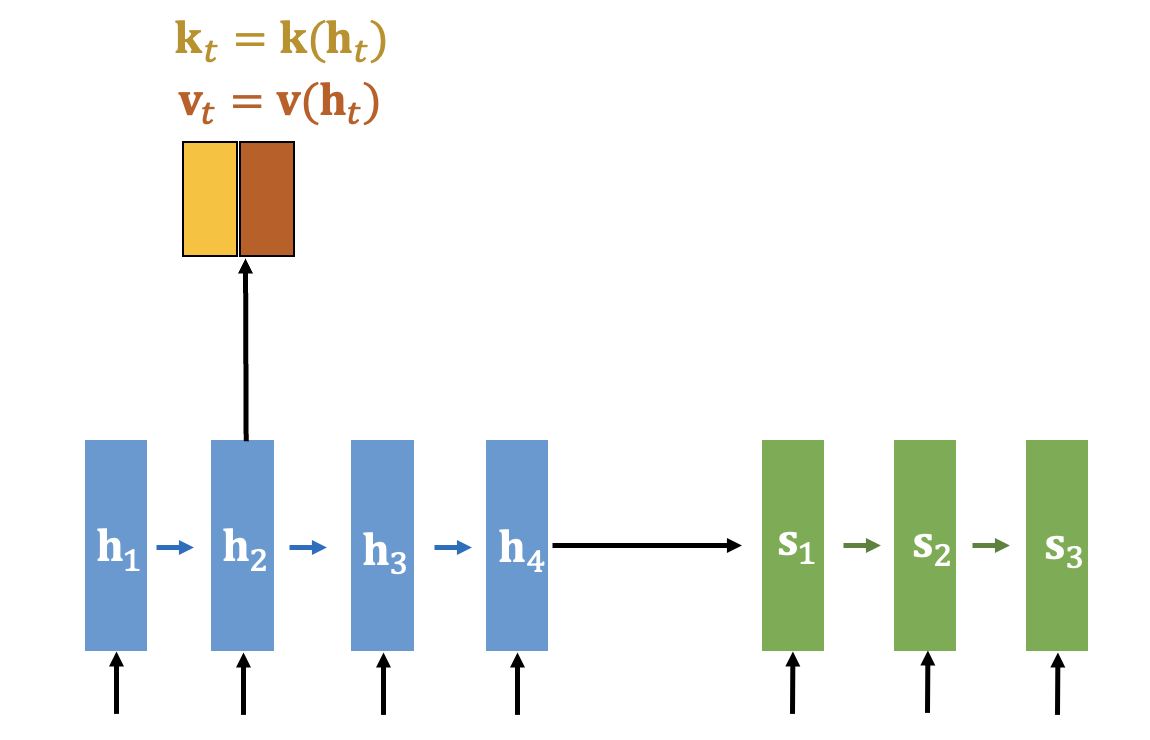
어텐션이 포함된 seq2seq 모델의 인코더는 기존 인코더와 유사하게 작동한다. 다만 추가적으로 매 시간스텝 \(t\) 마다 은닉상태 \(\mathbf{h}_t\) 를 이용하여 키(key)와 밸류(value)를 생성한다.
\[ \mathbf{k}_t= \mathbf{k}(\mathbf{h}_t ), \ \ \ \ \ \mathbf{v}_t= \mathbf{v}( \mathbf{h}_t) \]
키(key) \(\mathbf{k}_t\) 와 밸류(value) \(\mathbf{v}_t\) 는 은닉상태의 선형 또는 비선형 함수로 생성할 수 있지만 일반적으로 은닉상태를 그대로 키(key)와 밸류(value)로 사용한다. 만약 key-value를 선형 또는 비선형 함수로 생성한다면 이 함수들은 물론 학습 대상이다. 어텐션 방법에는 여러가지 변이(variant)가 있고 있을 수 있다. 이는 자연법칙이 아니라 알고리즘이므로 당연한 일이다.
인코더 모델을 Tensorflow2로 구현하면 다음과 같다.
class Encoder(Model):
def __init__(self, hidden_state_dim):
super(Encoder, self).__init__()
self.lstm = LSTM(units=hidden_state_dim, return_sequences=True, return_state=True)
def call(self, enc_input):
# enc_hiddens=(batch, seq_len, hidden_dim),
# h_st=(batch, hidden_dim), c_st=(batch, hidden_dim)
enc_hiddens, h_st, c_st = self.lstm(enc_input)
enc_states = [h_st, c_st]
return enc_hiddens, enc_states
return_sequences와 return_state를 모두 True로 설정하여 각 시간스텝마다 은닉상태를 출력하고 마지막 은닉 상태, 마지막 셀상태 값을 출력하도록 하였다.
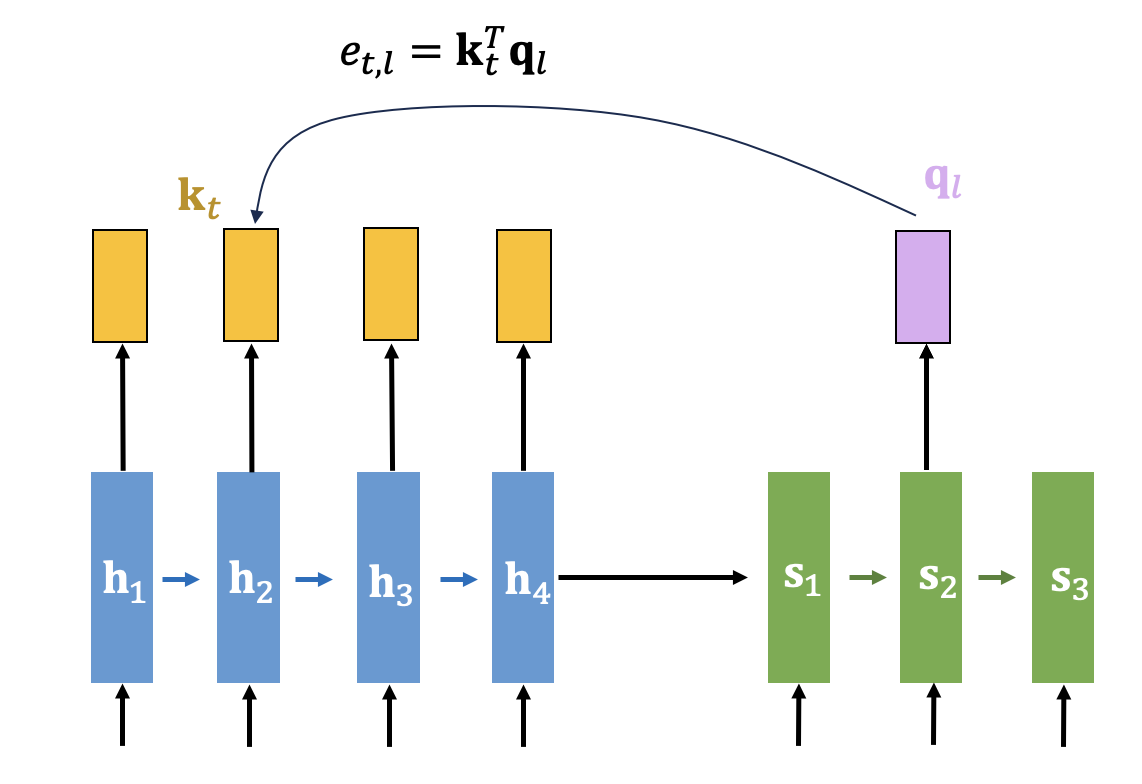
디코딩의 특정 시간스텝에서 필요한 정보를 인코더가 가지고 있는지 여부를 인코더의 각 스텝에 질의(query)하면 어텐션 매커니즘이 디코더의 질의(query)에 대해 인코더의 키(key)를 모두 비교하여 유사한 정도를 점수(score)로 계산하게 되는데 이를 구체적으로 알아보자. 일반적으로 질의(query) 벡터 \(\mathbf{q}_l\) 은 해당 시간스텝의 디코더 은닉상태를 그대로 사용한다.
디코더 시간스텝 \(l\) 에서의 질의(query) 벡터와 인코더 시간스텝 \(t\) 에서의 키(key) 벡터의 유사도를 나타내는 어텐션 점수(attention score) \(e_{t,l}\) 은 여러가지 방식으로 계산할 수 있다. 대표적인 것으로는 dot, general, concat 방식이 있는데 각각 아래 식과 같다.
\[ \begin{align} & \mbox{dot: } \ e_{t,l}= \mathbf{k}_t^T \mathbf{q}_l \\ \\ & \mbox{general: } \ e_{t,l}= \mathbf{k}_t^T W_g \mathbf{q}_l \\ \\ & \mbox{concat: } \ e_{t,l}= V^T \tanh (W_1 \mathbf{k}_t+W_2 \mathbf{q}_l ) \end{align} \]
여기서 행렬 \(W_g, \ W_1, \ W_2, \ V\) 등은 모두 학습 대상이다. dot, general은 루옹(Luong)이, concat 은 바다나우(Bahdanau)가 제안하였다.
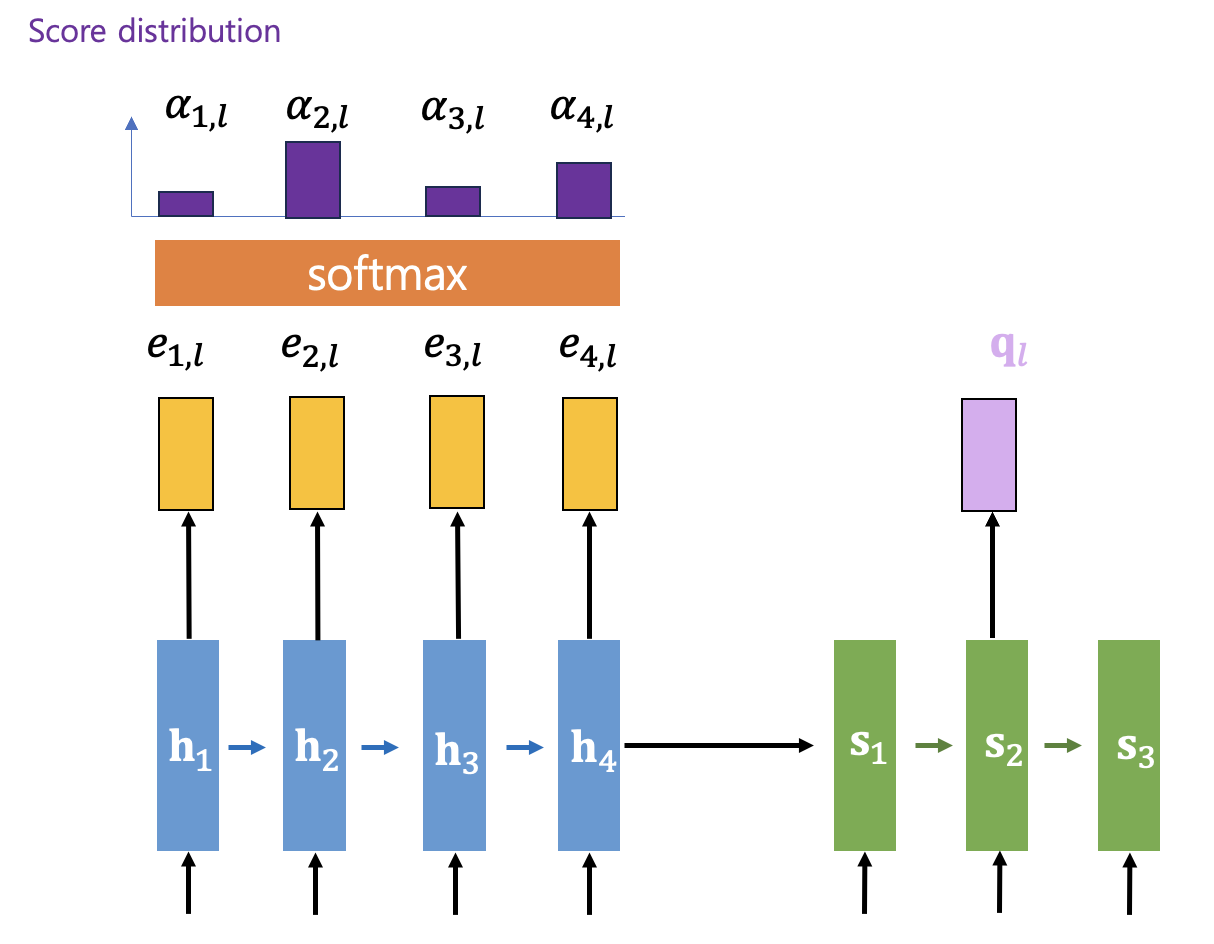
인코더의 모든 시간스텝에서 계산한 어텐션 점수는 소프트맥스(softmax) 함수를 통해 인코더의 모든 시간스텝에 대한 일종의 확률분포로 만든다. 이 확률 값 \(\alpha_{t,l} \) 을 어텐션 점수분포(attention score distribution) 또는 어텐션 가중값(weighting) 이라고 한다.
\[ \alpha_{t,l}= softmax (e_{t,l} )= \frac{ \exp (e_{t,l} ) }{ \sum_{t'} \exp ( e_{t',l} ) } \]
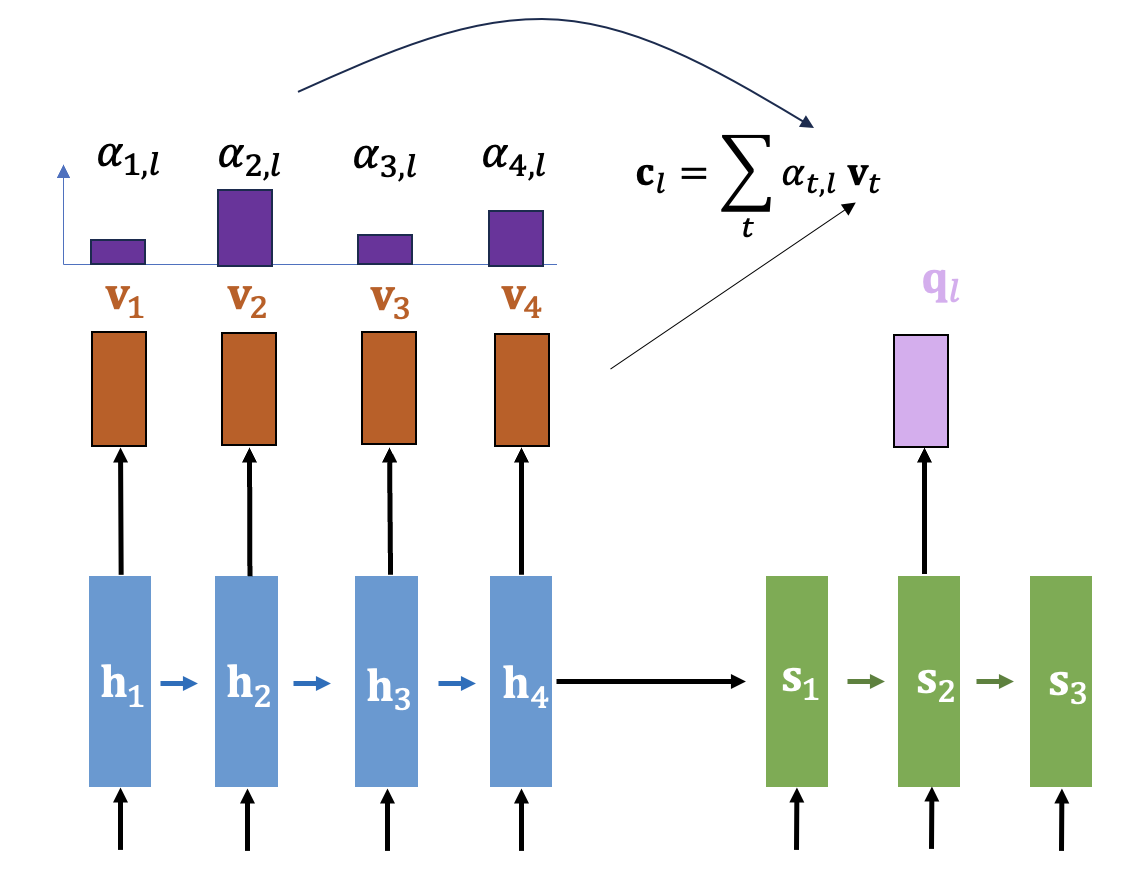
이제 디코더 시간스텝 \(l\) 에서의 질의(query)에 대한 답신으로서 다음과 같이 컨텍스트 벡터 \(\mathbf{c}_l\) 을 계산해서 디코더로 보내준다. 컨텍스트 벡터는 점수분포 \(\alpha_{t,l}\) 과 인코더의 밸류(value)벡터 \(\mathbf{v}_t\) 의 가중합으로 계산한다.
\[ \mathbf{c}_l= \sum_t \alpha_{t,l} \mathbf{v}_t \]
어텐션 모듈을 Tensorflow2로 구현하면 다음과 같다. 여기서는 키(key)와 밸류(value) 벡터로서 인코더의 은닉상태를, 질의(query) 벡터로서 디코더의 은닉상태를 사용했다. 그리고 어텐션 점수(attention score) 계산에는 concat 방식을 사용했다.
class AdAttention(Layer):
def __init__(self, attn_units):
super(AdAttention, self).__init__()
self.W1 = Dense(attn_units, use_bias=False) # key
self.W2 = Dense(attn_units, use_bias=False) # query
self.V = Dense(1, use_bias=False)
def call(self, enc_hiddens, dec_hidden):
# enc_hiddens = (batch, seq_len, hidden_state_dim)
# dec_hidden = (batch, hidden_state_dim)
# dec_hidden_exp = (batch, 1, hidden_state_dim)
dec_hidden_exp = tf.expand_dims(dec_hidden, 1)
keys = self.W1(enc_hiddens) # (batch, seq_len, attn_units)
query = self.W2(dec_hidden_exp) # (batch, 1, attn_units)
values = enc_hiddens
tanh_output = tf.nn.tanh(keys + query)
score = self.V(tanh_output) # (batch, seq_len, 1)
attention_weights = tf.nn.softmax(score, axis=1) # (batch, seq_len, 1)
context_vec = attention_weights * values # (batch, seq_len, hidden_dim)
context_vec = tf.reduce_sum(context_vec, axis=1) # (batch, hidden_dim)
return context_vec
컨텍스트 벡터 \(\mathbf{c}_l\) 을 수신한 디코더의 시간스텝 \(l\) 에서는 디코더의 은닉상태 \(\mathbf{s}_l\) 과 \(\mathbf{c}_l\) 을 결합(concatenation)하여 출력을 계산한다. 기존 seq2seq의 디코더에서는 은닉상태 \(\mathbf{s}_l\) 만을 이용하여 출력을 계산했다는 점에서 차이가 있다.

이제 디코더의 시간스텝 \(l=1\) 부터 \(l=m\) 까지 위와 같은 과정을 반복하여 출력 시퀀스를 계산하면 된다.
어텐션이 포함된 디코더 모델을 Tensorflow2로 구현하면 다음과 같다.
class Decoder(Model):
def __init__(self, n_tokens, attn_units, hidden_state_dim):
super(Decoder, self).__init__()
self.lstm = LSTM(units=hidden_state_dim, return_sequences=True, return_state=True)
self.attention = AdAttention(attn_units)
self.fc = Dense(n_tokens, activation='softmax')
def call(self, dec_input, enc_hiddens, enc_states):
# enc_hiddens = [h1, h2, ..., hn] = (batch, seq_len, hidden_state_dim)
# dec_input=(batch, seq_len_dec, n_tokens)
# enc_states = [h_st, c_st]
dec_hiddens, h_st, c_st = self.lstm(dec_input, initial_state=enc_states)
seq_len_dec = tf.shape(dec_hiddens)[1]
# Use tf.TensorArray to handle dynamic loops in TensorFlow
dec_out_array = tf.TensorArray(dtype=tf.float32, size=seq_len_dec, dynamic_size=True)
for t in tf.range(seq_len_dec):
dec_hidden_t = dec_hiddens[:, t, :]
context_vec = self.attention(enc_hiddens, dec_hidden_t)
out = tf.concat([dec_hidden_t, context_vec], axis=-1)
dec_out_t = self.fc(out) # (batch, n_tokens)
dec_out_array = dec_out_array.write(t, dec_out_t)
dec_out = dec_out_array.stack() # Convert TensorArray to tensor
dec_out = tf.transpose(dec_out, perm=[1, 0, 2]) # Transpose to get (batch, seq_len_dec, n_tokens)
return dec_out, h_st, c_st
인코더와 어텐션, 그리고 디코더를 연결하여 어텐션이 포함된 seq2seq 모델을 Tensorflow2로 구현하면 다음과 같다.
class Seq2seqAttn(Model):
def __init__(self, n_tokens, attn_units, hidden_state_dim):
super(Seq2seqAttn, self).__init__()
self.encoder = Encoder(hidden_state_dim)
self.decoder = Decoder(n_tokens, attn_units, hidden_state_dim)
def call(self, enc_dec_input):
enc_input = enc_dec_input[0]
dec_input = enc_dec_input[1]
enc_hiddens, enc_states = self.encoder(enc_input)
dec_out, _, _ = self.decoder(dec_input, enc_hiddens, enc_states)
return dec_out
성능을 테스트하기 위하여 앞서 살펴본 5자리의 입력 숫자열을 반대 순서로 정렬된 숫자열로 변환하여 출력시키는 seq2seq예제 (https://pasus.tistory.com/290)에서 입력 숫자열 길이를 10으로 두 배 늘린 문제에 어텐션이 포함된 seq2seq 모델을 적용해보겠다. 데이터셋 5000개로 이폭 50으로 학습한 결과는 다음과 같다.
Epoch 45/50
125/125 - 12s - loss: 0.0094 - accuracy: 0.9999 - val_loss: 0.0099 - val_accuracy: 0.9999 - 12s/epoch - 97ms/step
Epoch 46/50
125/125 - 12s - loss: 0.0082 - accuracy: 0.9999 - val_loss: 0.0086 - val_accuracy: 0.9999 - 12s/epoch - 97ms/step
Epoch 47/50
125/125 - 12s - loss: 0.0075 - accuracy: 0.9999 - val_loss: 0.0080 - val_accuracy: 0.9999 - 12s/epoch - 97ms/step
Epoch 48/50
125/125 - 12s - loss: 0.0071 - accuracy: 0.9999 - val_loss: 0.0094 - val_accuracy: 0.9995 - 12s/epoch - 97ms/step
Epoch 49/50
125/125 - 12s - loss: 0.0253 - accuracy: 0.9948 - val_loss: 0.0105 - val_accuracy: 0.9993 - 12s/epoch - 96ms/step
Epoch 50/50
125/125 - 12s - loss: 0.0073 - accuracy: 0.9999 - val_loss: 0.0068 - val_accuracy: 0.9999 - 12s/epoch - 96ms/step
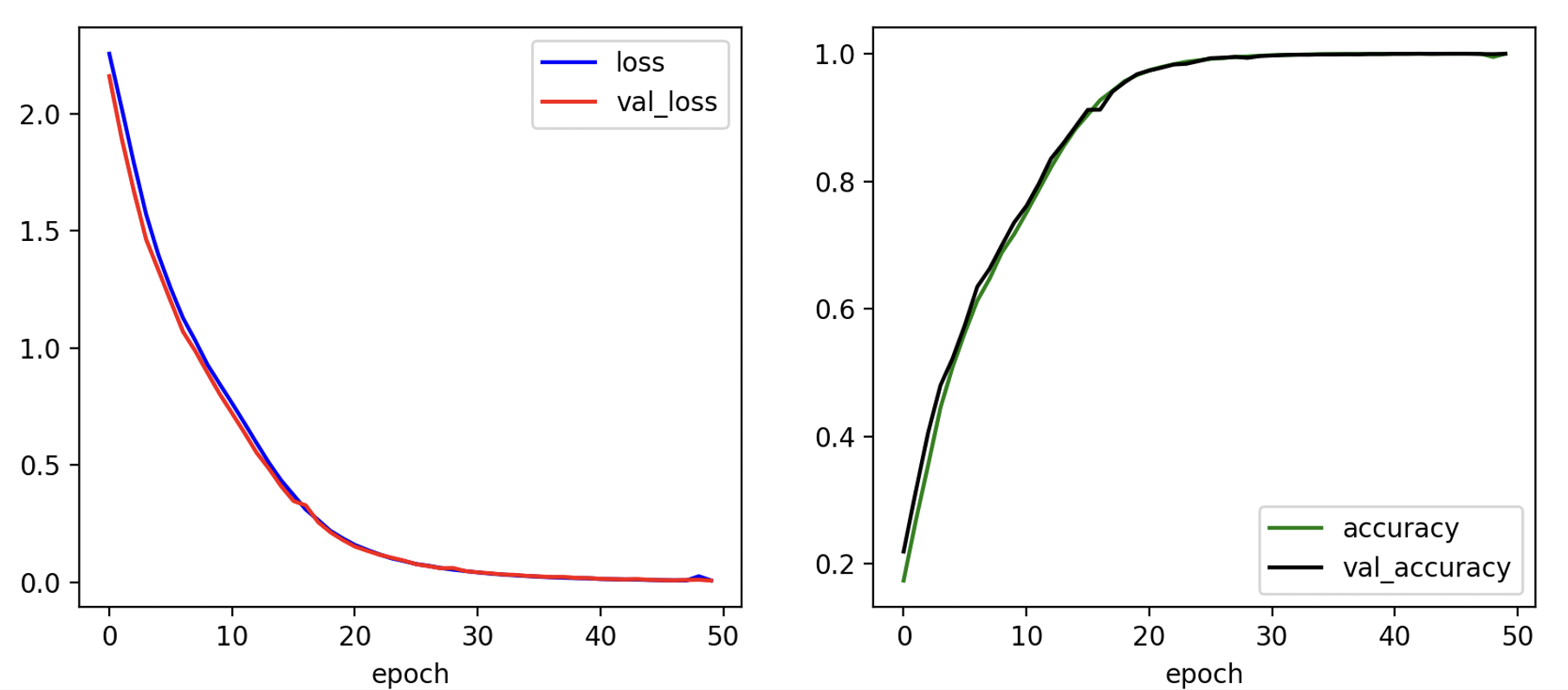
다음은 임의로 생성된 10개의 시퀀스 데이터에 대해서 테스트한 결과다. 출력 시퀀스의 정확도가 100%로서 어텐션이 포함된 seq2seq의 정확도가 기존 seq2seq의 정확도를 크게 앞지르는 것을 알 수 있다.
Input Exact Predicted T/F
[8, 7, 3, 5, 4, 3, 6, 0, 9, 3] [3, 9, 0, 6, 3, 4, 5, 3, 7, 8] [3, 9, 0, 6, 3, 4, 5, 3, 7, 8] True
[4, 5, 3, 3, 0, 5, 4, 4, 3, 8] [8, 3, 4, 4, 5, 0, 3, 3, 5, 4] [8, 3, 4, 4, 5, 0, 3, 3, 5, 4] True
[9, 2, 9, 1, 3, 2, 0, 4, 8, 7] [7, 8, 4, 0, 2, 3, 1, 9, 2, 9] [7, 8, 4, 0, 2, 3, 1, 9, 2, 9] True
[0, 5, 4, 3, 5, 0, 6, 2, 5, 0] [0, 5, 2, 6, 0, 5, 3, 4, 5, 0] [0, 5, 2, 6, 0, 5, 3, 4, 5, 0] True
[8, 7, 0, 9, 6, 0, 8, 4, 3, 1] [1, 3, 4, 8, 0, 6, 9, 0, 7, 8] [1, 3, 4, 8, 0, 6, 9, 0, 7, 8] True
[9, 5, 7, 7, 5, 2, 2, 0, 8, 7] [7, 8, 0, 2, 2, 5, 7, 7, 5, 9] [7, 8, 0, 2, 2, 5, 7, 7, 5, 9] True
[3, 1, 3, 8, 5, 9, 4, 9, 7, 8] [8, 7, 9, 4, 9, 5, 8, 3, 1, 3] [8, 7, 9, 4, 9, 5, 8, 3, 1, 3] True
[4, 3, 4, 8, 4, 1, 0, 2, 1, 7] [7, 1, 2, 0, 1, 4, 8, 4, 3, 4] [7, 1, 2, 0, 1, 4, 8, 4, 3, 4] True
[8, 4, 1, 7, 1, 9, 2, 7, 0, 3] [3, 0, 7, 2, 9, 1, 7, 1, 4, 8] [3, 0, 7, 2, 9, 1, 7, 1, 4, 8] True
[5, 5, 3, 6, 2, 3, 3, 3, 2, 4] [4, 2, 3, 3, 3, 2, 6, 3, 5, 5] [4, 2, 3, 3, 3, 2, 6, 3, 5, 5] True
Accuracy: 1.0
다음은 Tensorflow2 전체 코드다.
s2s_attn_model.py
# Seq2Seq with Attention model
# coded by st.watermelon
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Layer, LSTM, Dense, Input
class Encoder(Model):
def __init__(self, hidden_state_dim):
super(Encoder, self).__init__()
self.lstm = LSTM(units=hidden_state_dim, return_sequences=True, return_state=True)
def call(self, enc_input):
# enc_hiddens=(batch, seq_len, hidden_dim),
# h_st=(batch, hidden_dim), c_st=(batch, hidden_dim)
enc_hiddens, h_st, c_st = self.lstm(enc_input)
enc_states = [h_st, c_st]
return enc_hiddens, enc_states
class AdAttention(Layer):
def __init__(self, attn_units):
super(AdAttention, self).__init__()
self.W1 = Dense(attn_units, use_bias=False) # key
self.W2 = Dense(attn_units, use_bias=False) # query
self.V = Dense(1, use_bias=False)
def call(self, enc_hiddens, dec_hidden):
# enc_hiddens = (batch, seq_len, hidden_state_dim)
# dec_hidden = (batch, hidden_state_dim)
# dec_hidden_exp = (batch, 1, hidden_state_dim)
dec_hidden_exp = tf.expand_dims(dec_hidden, 1)
keys = self.W1(enc_hiddens) # (batch, seq_len, attn_units)
query = self.W2(dec_hidden_exp) # (batch, 1, attn_units)
values = enc_hiddens
tanh_output = tf.nn.tanh(keys + query)
score = self.V(tanh_output) # (batch, seq_len, 1)
attention_weights = tf.nn.softmax(score, axis=1) # (batch, seq_len, 1)
context_vec = attention_weights * values # (batch, seq_len, hidden_dim)
context_vec = tf.reduce_sum(context_vec, axis=1) # (batch, hidden_dim)
return context_vec
class Decoder(Model):
def __init__(self, n_tokens, attn_units, hidden_state_dim):
super(Decoder, self).__init__()
self.lstm = LSTM(units=hidden_state_dim, return_sequences=True, return_state=True)
self.attention = AdAttention(attn_units)
self.fc = Dense(n_tokens, activation='softmax')
def call(self, dec_input, enc_hiddens, enc_states):
# enc_hiddens = [h1, h2, ..., hn] = (batch, seq_len, hidden_state_dim)
# dec_input=(batch, seq_len_dec, n_tokens)
# enc_states = [h_st, c_st]
dec_hiddens, h_st, c_st = self.lstm(dec_input, initial_state=enc_states)
seq_len_dec = tf.shape(dec_hiddens)[1]
# Use tf.TensorArray to handle dynamic loops in TensorFlow
dec_out_array = tf.TensorArray(dtype=tf.float32, size=seq_len_dec, dynamic_size=True)
for t in tf.range(seq_len_dec):
dec_hidden_t = dec_hiddens[:, t, :]
context_vec = self.attention(enc_hiddens, dec_hidden_t)
out = tf.concat([dec_hidden_t, context_vec], axis=-1)
dec_out_t = self.fc(out) # (batch, n_tokens)
dec_out_array = dec_out_array.write(t, dec_out_t)
dec_out = dec_out_array.stack() # Convert TensorArray to tensor
dec_out = tf.transpose(dec_out, perm=[1, 0, 2]) # Transpose to get (batch, seq_len_dec, n_tokens)
return dec_out, h_st, c_st
class Seq2seqAttn(Model):
def __init__(self, n_tokens, attn_units, hidden_state_dim):
super(Seq2seqAttn, self).__init__()
self.encoder = Encoder(hidden_state_dim)
self.decoder = Decoder(n_tokens, attn_units, hidden_state_dim)
def call(self, enc_dec_input):
enc_input = enc_dec_input[0]
dec_input = enc_dec_input[1]
enc_hiddens, enc_states = self.encoder(enc_input)
dec_out, _, _ = self.decoder(dec_input, enc_hiddens, enc_states)
return dec_out
s2s_attn_train.py
# Seq2Seq with Attention train
# coded by st.watermelon
from s2s_attn_model import Seq2seqAttn
from gen_data import *
import os
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, LSTM, Dense
""" setup Seq2Seq with attention agent """
class S2sAttn_agent(Model):
def __init__(self, seq_len):
super(S2sAttn_agent, self).__init__()
# hyperparameters
self.TRAIN_SIZE = 5000
self.ATTN_UNITS = 12
self.SEQ_LEN = seq_len
self.N_TOKENS = 10
self.BATCH_SIZE = 32
self.HIDDEN_STATE_DIM = 16
self.LEARNING_RATE = 1e-3
# create seq2seq with attention
self.s2s = Seq2seqAttn(self.N_TOKENS, self.ATTN_UNITS, self.HIDDEN_STATE_DIM)
# compile
self.s2s.compile(
loss=tf.keras.losses.categorical_crossentropy,
optimizer=tf.keras.optimizers.Adam(self.LEARNING_RATE),
metrics=['accuracy']
)
encoder_input = Input((self.SEQ_LEN, self.N_TOKENS))
decoder_input = Input((self.SEQ_LEN, self.N_TOKENS))
self.s2s([encoder_input, decoder_input])
self.s2s.encoder.summary()
self.s2s.decoder.summary()
self.s2s.summary()
def train(self, epochs):
X_encoder, X_decoder, y = \
create_dataset(self.TRAIN_SIZE, self.SEQ_LEN, self.N_TOKENS, verbose=False)
history = self.s2s.fit(
[X_encoder, X_decoder],
y,
batch_size=self.BATCH_SIZE,
epochs=epochs,
validation_split=0.2,
verbose=2
)
# save
self.s2s.save_weights("./save_weights/s2s_attn.h5")
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r-', label='val_loss')
plt.xlabel('epoch')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(history.history['accuracy'], 'g-', label='accuracy')
plt.plot(history.history['val_accuracy'], 'k-', label='val_accuracy')
plt.xlabel('epoch')
plt.legend()
plt.show()
def decode_seq(self, input_seq, true_seq):
# input_seq=(seq_len, n_tokens)
# true_seq=(seq_len, n_tokens)
if os.path.exists('./save_weights/s2s_attn.h5'):
self.s2s.load_weights("./save_weights/s2s_attn.h5")
else:
return 0
print('Input \t\t\t\t Exact \t\t\t Predicted \t\tT/F')
correct = 0
n_seq = input_seq.shape[0]
for seq_idx in range(0, n_seq):
# take one sequence at a time
decoded_seq = self.single_decode_seq(
tf.reshape(input_seq[seq_idx], (1, self.SEQ_LEN, self.N_TOKENS)))
if (one_hot_decode(true_seq[seq_idx]) == decoded_seq):
correct += 1
print(one_hot_decode(input_seq[seq_idx]), '\t',
one_hot_decode(true_seq[seq_idx]), '\t', decoded_seq,
'\t', one_hot_decode(true_seq[seq_idx]) == decoded_seq)
print('Accuracy: ', correct / n_seq)
def single_decode_seq(self, single_input_seq):
# single_input_seq=(n_seq, seq_len, n_tokens)
# encode the input sequence as context vector
enc_hiddens, enc_states = self.s2s.encoder(single_input_seq)
# generate empty dec_input sequence of length 1.
dec_input_seq = np.zeros((1, 1, self.N_TOKENS)) # (1, seq_len, input_dim)
# make <sos>
dec_input_seq[0, 0, 0] = 1
# looping for a batch of sequences
stop_condition = False
decoded_seq = list()
while not stop_condition:
# decode the input
dec_out, h_st, c_st = self.s2s.decoder(dec_input_seq, enc_hiddens, enc_states)
# predict the decoder output using argmax
sampled_digit = np.argmax(dec_out[0, -1, :])
# add the predicted token/output to output sequence
decoded_seq.append(sampled_digit)
# stop condition: hit max length
if (len(decoded_seq) == self.SEQ_LEN):
stop_condition = True
# update the decoder input sequence for the next LSTM cell
dec_input_seq = np.zeros((1, 1, self.N_TOKENS))
dec_input_seq[0, 0, sampled_digit] = 1.
# update context value
enc_states = [h_st, c_st]
return decoded_seq
if __name__ == "__main__":
seq_len = 10
agent = S2sAttn_agent(seq_len)
agent.train(50)
s2s_attn_load_play.py
# Seq2Seq with Attention inference
# coded by st.watermelon
from s2s_attn_train import S2sAttn_agent
from gen_data import create_dataset
def main():
seq_len = 10
agent = S2sAttn_agent(seq_len)
input_seq, _, true_seq = create_dataset(10, seq_len, 10, verbose=False)
agent.decode_seq(input_seq, true_seq)
if __name__ == "__main__":
main()