오일러의 회전 정리 (Euler’s Rotation Theorem)

오일러각 좌표변환 방법에서 알아본 회전축은 좌표계의 \(x\) 축, \(y\) 축, \(z\) 축이었다. 하지만 좌표계를 구성하는 좌표축만이 아니라 임의의 축, 즉 임의의 방향을 중심으로 좌표계를 회전시킬 수도 있다.

 

 

단위벡터는 크기가 \(1\) 인 벡터이기 때문에 방향을 표시하는데 자주 쓰인다. 여기서도 회전축 방향을 정하는데 단위벡터를 이용하기로 하고 기호로 \(\hat{p}\) 으로 표시하기로 한다. 좌표계 \(\{a\}\) 를 회전축 \(\hat{p}\) 축을 중심으로 \(\beta\) 만큼 회전시키면 새로운 좌표계로 변환되는데 이 좌표계를 \(\{b\}\) 라고 하자.

 

 

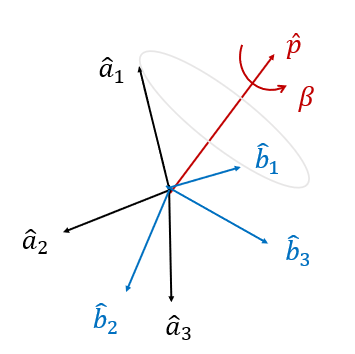
그러면 그림에서 보듯이 좌표계 \(\{a\}\) 의 좌표축과 회전축 사이의 각도는 좌표계 \(\{b\}\) 의 좌표축과 회전축 사이의 각도와 같다. \(\hat{p}\) 가 회전축이므로 이를 수식으로 표현하면 \(\hat{a}_i \cdot \hat{p}= \hat{b}_i \cdot \hat{p}, \ i=1,2,3\) 이다. 단위벡터 \(\hat{p}\) 을 좌표계 \(\{a\}\) 와 좌표계 \(\{b\}\) 로 표현하면 각각 \(\mathbf{p}^a\) 와 \(\mathbf{p}^b\) 인데, 이 경우에는 \(\mathbf{p}^a=\mathbf{p}^b\) 가 된다. 이제 좌표계 \(\{a\}\) 에서 좌표계 \(\{b\}\) 로의 DCM \(C_b^a\) 를 이용하여 \(\mathbf{p}^a\) 와 \(\mathbf{p}^b\) 의 관계식을 쓰면 다음과 같다.

 

\[ \begin{align} \mathbf{p}^a &=C_b^a \mathbf{p}^b \tag{1} \\ \\ &=C_b^a \mathbf{p}^a \end{align} \]

 

\( C_b^a\) 는 \(3 \times 3\) 행렬이고 \(\mathbf{p}^a\) 는 \( 3 \times 1\) 벡터다. 위 식이 말하는 것은 무엇일까? 행렬 \(C_b^a\) 는 고유값(eigenvalue) \(+1\) 을 갖고 그에 해당하는 고유벡터(eigenvector)는 \(\mathbf{p}^a\) 라는 것이다.

그렇다면 모든 DCM이 고유값 \(+1\) 을 갖고 그에 해당하는 고유벡터는 회전축이 될까? 좌표계 \(\{a\}\) 에서 좌표계 \(\{b\}\) 로의 DCM \(C_b^a\) 의 고유값 \(+1\) 에 해당하는 고유벡터가 한번의 회전을 통하여 좌표계 \(\{a\}\) 에서 좌표계 \(\{b\}\) 로 변환시킬 수 있는 회전축이라는 뜻으로 일반화시켜도 될까? DCM은 연쇄법칙이 적용되므로 다양한 좌표축을 중심으로 여러 번의 회전을 통하여얻은 좌표변환도 한 개의 행렬로 표현할 수 있다. 만약 그렇다면,

"모든 좌표변환은 DCM의 고유값 \(+1\) 에 해당하는 고유벡터를 중심으로 한 번의 회전으로 얻은 좌표변환과 같다."

라고 해도 될 것이다. 이것이 오일러의 회전 정리(Euler's rotation theorem)다.

그럼 이를 증명해 보도록 하자. 증명 과정에서 표기를 단순하게 하기 위하여 DCM에 좌표계를 명기하지 않고 그냥 \(C\) 로 쓰겠다. 먼저 DCM은 단위 직교 행렬이라는 특성이 있다. 즉

 

\[ C^T C=I \tag{2} \]

 

이다. 단위 직교 행렬의 행렬식(determinant)은 다음과 같이 계산할 수 있다.

 

\[ \begin{align} 1 &= det⁡(C^T C)=det⁡(C^T ) \ det⁡(C) \tag{3} \\ \\ &= \left( det⁡(C) \right)^2 \end{align} \]

 

따라서 \(det⁡(C)= \pm 1\) 이다. 하지만 DCM의 경우는 \(det⁡(C)=1\) 이다. 그래서 DCM을 단위 직교 행렬의 특수한 종류(SO, special orthogonal group)라고 한다. \(det⁡(C)=-1\) 인 경우 행렬 \(C\) 를 회전반사(rotation-reflection) 행렬 또는 부적절한 회전(improper rotation) 행렬이라고 한다.

 

 

\(det⁡(C)=1\) 이면, 다음식이 성립한다.

 

\[ \begin{align} det⁡(C-I) &= det⁡(C-CC^T ) \tag{4} \\ \\ &=det⁡(C(I-C^T ))=det⁡(C) \ det⁡(I-C^T ) \\ \\ &= -det⁡(C) \ det⁡(C^T-I) \\ \\ &= -det⁡(C-I) \end{align} \]

 

따라서 \(det⁡(C-I)=0\) 이 된다. 이는 곧 다음식을 만족하는 \(\mathbf{v} \ne 0\) 인 어떤 벡터가 존재함을 의미한다.

 

\[ C \mathbf{v} = \mathbf{v} \tag{5} \]

 

따라서 행렬 \(C\) 는 값이 \(+1\) 인 고유값을 가지며 그에 해당하는 고유벡터는 \(\mathbf{v}\) 다. 벡터 \(\mathbf{v}\) 는 DCM \(C\)로 주어지는 좌표변환에도 그 값이 변하지 않으므로 회전축이다. 이로써 오일러의 회전 정리가 증명되었다.

그럼 DCM의 행렬식이 \(+1\) 임을 증명해 보자. DCM \(C_b^a\) 의 정의에 의하면,

 

\[ C_b^a= \begin{bmatrix} \hat{a}_1 \cdot \hat{b}_1 & \hat{a}_1 \cdot \hat{b}_2 & \hat{a}_1 \cdot \hat{b}_3 \\ \hat{a}_2 \cdot \hat{b}_1 & \hat{a}_2 \cdot \hat{b}_2 & \hat{a}_2 \cdot \hat{b}_3 \\ \hat{a}_3 \cdot \hat{b}_1 & \hat{a}_3 \cdot \hat{b}_2 & \hat{a}_3 \cdot \hat{b}_3 \end{bmatrix} \tag{6} \]

 

이다. 따라서 DCM의 첫 번째 열은 \(\hat{b}_1\) 을 좌표계 \(\{a\}\) 로 표현한 것이므로 \(\mathbf{b}_1^a\) 로 쓸 수 있고, 두 번째 열, 세 번째 열도 마찬가지로 각각 \(\mathbf{b}_2^a\), \(\mathbf{b}_3^a\) 로 쓸 수 있다. 즉 DCM은 각 열이 좌표계 \(\{b\}\) 의 축을 이루는 각각의 단위벡터를 좌표계 \(\{a\}\) 로 표현한 열벡터로 구성되어 있다. 따라서 다음 식이 성립한다.

 

\[ C_b^a= \begin{bmatrix} \mathbf{b}_1^a & \mathbf{b}_2^a & \mathbf{b}_3^a \end{bmatrix} \tag{7} \]

 

한편, 행렬식은 행렬의 각 열벡터를 이용하면 다음과 같이 계산되므로 DCM의 행렬식은 \(+1\) 이 됨을 알 수 있다.

 

\[ \begin{align} det⁡(C_b^a ) &= \mathbf{b}_1^a \cdot \left( \mathbf{b}_2^a \times \mathbf{b}_3^a \right) \tag{8} \\ \\ &= \mathbf{b}_1^a \cdot \mathbf{b}_1^a=1 \end{align} \]

 

 

방향코사인행렬, 오일러각, 그리고 쿼터니언