\(m\)개의 n차원 데이터 \(\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, ..., \mathbf{x}^{(m)} \in \mathbb{R}^n\) 이 주어졌다고 하자. 이 데이터를 d차원 공간에 투사해서 차원(dimension)을 축소하는 것이 목적이다.
그렇다면 n차원의 부분 공간인 d차원 (\(d \lt n\))에서 직교 좌표축의 방향을 어떻게 결정해야 데이터의 정보 손실을 최소화할 수 있을까. 다음 그림은 2차원 데이터의 예를 도시한 것이다.
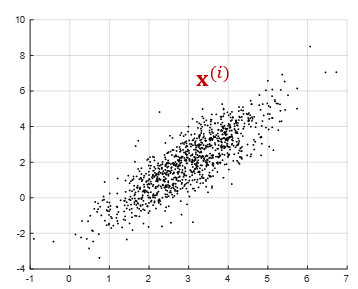
우선 새로운 좌표축의 원점을 \(m\)개 데이터의 평균점 \(\mathbf{\mu}\)에 위치시키도록 하자.
\[ \mathbf{\mu} = \frac{1}{m} \sum_{i=1}^m \mathbf{x}^{(i)} \]
그리고 모든 데이터 \(\mathbf{x}^{(i)}\)를 n차원의 공간에서 서로 직각인 벡터 d개의 단위 벡터 \(\mathbf{w}_1, \mathbf{w}_2, ..., \mathbf{w}_d\) 로 이루어진 d차원 부분 공간에 투사한다. 투사된 데이터를 \(\hat{\mathbf{x}}^{(i)}\) 라고 한다면 다음 식이 성립한다.
\[ \sum_{i=1}^m \lVert \mathbf{x}^{(i)} -\mathbf{\mu} \rVert_2^2 = \sum_{i=1}^m \lVert \hat{\mathbf{x}}^{(i)} -\mathbf{\mu} \rVert_2^2 + \sum_{i=1}^m \lVert \mathbf{x}^{(i)} - \hat{\mathbf{x}}^{(i)} \rVert_2^2 \]
위 식의 왼쪽항은 데이터셋이 주어지면 정해지는 값(상수)이며 오른쪽 항에서 첫번째 항은 투사된 데이터의 분산을 나타내고 두번째 항은 투사 오차(projection error)를 나타낸다.

따라서 투사 오차를 최소화하는 것은 곧 투사 분산을 최대화하는 것과 동일하다. 아래 그림과 같이 2차원 데이터 예에서는 데이터가 더 넓게 분포된 방향으로 새로운 좌표축을 설정하면 투사 오차가 최소화될 것 같다.
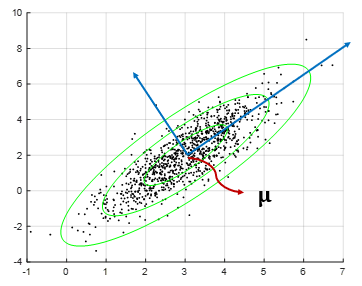
주성분 분석(PCA)은 투사 오차를 최소화하도록 또는 투사 분산을 최대화하도록 d차원 부분 공간의 좌표축 벡터인 \( \mathbf{w}_1, \mathbf{w}_2, ..., \mathbf{w}_d\) 를 결정하는 알고리즘이다.
\[ \begin{align} \mathbf{x}^{(i)} - \mathbf{\mu} & \approx z_{i1} \mathbf{w}_1+ z_{i2} \mathbf{w}_2 + \cdots + z_{id} \mathbf{w}_d \\ \\ & = \begin{bmatrix} \mathbf{w}_1 & \mathbf{w}_2 & \cdots & \mathbf{w}_d \end{bmatrix} \begin{bmatrix} z_{i1} \\ z_{i2} \\ \vdots \\ z_{id} \end{bmatrix} \\ \\ & = W \mathbf{z}_i \end{align} \]
여기서 \(z_{ij}\)는 \((\mathbf{x}^{(i)}- \mathbf{\mu})\)의 \(\mathbf{w}_j\)축 성분으로서 \(z_{ij}=\mathbf{w}_j^T (\mathbf{x}^{(i)}-\mathbf{\mu})\) 로 주어지며,
\[ \mathbf{z}_i= W^T (\mathbf{x}^{(i) } - \mathbf{\mu} ) \]
이다.

\( W \in \mathbb{R}^{n \times d}\)는 서로 직각인 단위 벡터(orthonormal vectors)로 이루어진 행렬로서 다음 식을 만족한다.
\[ W^T W=I_d \]
여기서 문제는 투사 오차가 최소가 되도록 행렬 \(W\)를 어떻게 결정하는가에 있다.

이 문제를 다음과 같이 최적화 문제로 정식화 해보자.
\[ \begin{align} & \arg\min_W J = \sum_{i=1}^m \lVert \mathbf{x}^{(i)}- \mathbf{\mu}- WW^T ( \mathbf{x}^{(i)}- \mathbf{\mu} ) \rVert_2^2 \\ \\ & \mbox{subject to } \ \ W^T W=I_d \end{align} \]
여기서 \(\mathbf{y}^{(i)}=\mathbf{x}^{(i) }- \mathbf{\mu}\) 로 치환하면 함수 \(J\)는 다음과 같이 쓸 수 있다.
\[ J = \sum_{i=1}^m \lVert \mathbf{y}^{(i)}- WW^T \mathbf{y}^{(i)} \rVert_2^2 \]
이제 평균점으로 조정된 데이터셋 \(\mathbf{y}^{(i)}\)을 열(column)로 하는 스냅샷(snapshot) 행렬을 다음과 같이 정의한다.
\[ Y= \begin{bmatrix} \mathbf{y}^{(1) } & \mathbf{y}^{(2) } & \cdots & \mathbf{y}^{(m) } \end{bmatrix} \in \mathbb{R}^{n \times m} \]
그러면 함수 \(J\)를 다음과 같이 스냅샷 행렬을 이용하여 표현할 수 있다.
\[ \begin{align} J &= \sum_{i=1}^m \lVert \mathbf{y}^{(i)}- WW^T \mathbf{y}^{(i)} \rVert_2^2 \\ \\ &= trace \left[ (Y-WW^T Y)^T (Y-WW^T Y) \right] \\ \\ &= trace \left[ Y^T (I_n-WW^T )^T (I_n-WW^T )Y \right] \end{align} \]
여기서
\[ \begin{align} (I_n-WW^T )^T (I_n-WW^T ) &=(I_n-WW^T )(I_n-WW^T ) \\ \\ &=I_n-WW^T \end{align} \]
가 성립하므로 위 식은 다음과 같이 된다.
\[ \begin{align} J &= trace \left[ Y^T (I_n-WW^T )Y \right] \\ \\ &=trace \left[ YY^T (I_n-WW^T ) \right] \\ \\ &=trace \left[ YY^T \right] - trace \left[ YY^T WW^T \right] \\ \\ &=trace \left[ YY^T \right]- trace \left[ W^T YY^T W \right] \end{align} \]
따라서 원래의 최적화 문제는 다음과 같이 쓸 수 있다.
\[ \begin{align} & \arg\min_W J = trace \left[ YY^T \right] -trace \left[ W^T YY^T W \right] \\ \\ & \mbox{subject to } \ \ W^T W=I_d \end{align} \]
그런데 여기서 \(Y\)는 \(W\)에 종속적이지 않으므로, 최소화 문제는 다음과 같이 최대화 문제로 바뀌게 된다.
\[ \begin{align} \arg\min_W \left( trace [ YY^T ]- trace [W^T YY^T W ] \right) &= \arg\min_W \left( - trace [W^T YY^T W ] \right) \\ \\ &= \arg\max_W \left( trace [W^T YY^T W ] \right) \end{align} \]
정리하면 PCA문제는 다음 최적화 문제로 바꿀 수 있다.
\[ \begin{align} & \arg\max_W \left( trace [W^T YY^T W ] \right) \\ \\ & \mbox{subject to } \ \ W^T W=I_d \end{align} \]
라그랑지 곱수 \(\lambda_{ij}\)를 이용하여 제약조건이 없는 최적화 문제로 바꾸면 다음과 같다.
\[ \arg\max_W L = trace [W^T YY^T W ] + \sum_{i=1}^d \sum_{j=1}^d \lambda_{ij} ( \delta_{ij}-\mathbf{w}_i^T \mathbf{w}_j ) \]
여기서
\[ \delta_{ij}= \begin{cases} 1, & i=j \\ 0, & i \ne j \end{cases} \]
이다. 최적화의 필요조건에 의하면 다음 미분식을 만족해야 한다.
\[ \begin{align} & \frac{\partial L}{\partial \mathbf{w}_i} = 2YY^T \mathbf{w}_i - 2 \lambda_{ii} \mathbf{w}_i - \sum_{j=1,i \ne j}^d \lambda_{ij} \mathbf{w}_j =0 \\ \\ & \frac{\partial L}{\partial \lambda_{ij}} = \delta_{ij} - \mathbf{w}_i^T \mathbf{w}_j =0 \end{align} \]
여기서 다음 행렬에 관한 미분식을 이용하였다.
\[ \frac{\partial (trace[A^T B A ])}{\partial A} =(B+B^T )A \]
정리하면 \(\mathbf{w}_i\)와 라그랑지 곱수 \(\lambda_{ij}\)는 다음 식을 만족해야 한다.
\[ \begin{align} & YY^T \mathbf{w}_i = \lambda_{ii} \mathbf{w}_i \\ \\ & \lambda_{ij}=0, \ \ \mbox{if} \ \ i \ne j \end{align} \]
따라서 라그랑지 곱수 \(\lambda_{ii}\)와 \(\mathbf{w}_i\)는 각각 행렬 \(YY^T\)의 고유값과 고유벡터가 됨을 알 수 있다.
이제 행렬 \(YY^T\)의 고유값과 고유벡터를 계산하면 주성분 분석(PCA) 문제를 풀 수 있다. 먼저 스냅샷 행렬 \(Y\)의 특이값 분해(SVD, singular value decomposition)을 구해보자.
\[ Y=U \Sigma V^T \]
여기서 \(U= \begin{bmatrix} \mathbf{u}_1 & \cdots & \mathbf{u}_n \end{bmatrix}\) 는 \( n \times n\) 직각 행렬(orthogonal matrix)이고 \(V= \begin{bmatrix} \mathbf{v}_1 & \cdots & \mathbf{v}_m \end{bmatrix}\) 는 \(m \times m\) 직각 행렬이며 \(\Sigma\) 는 \(n \times m\) 인 '대각' 행렬이다. 여기서 말하는 '대각' 행렬은 행과 열의 번호가 같은 성분만 \(0\)이 아닌 어떤 값을 갖는다는 의미다.
\(U\)와 \(V\)가 각각 직각 행렬이므로 다음 식을 만족한다.
\[ U^{ -1}=U^T, \ \ \ V^{ -1}=V^T \]
행렬 \(\Sigma\)의 대각 성분에 있는 \(0\)이 아닌 값은 행렬의 특이값 \(\sigma_i\)이다.
행렬 \(YY^T\)의 고유값과 고유벡터는 특이값 분해를 이용하여 다음과 같이 구할 수 있다.
\[ YY^T=U \Sigma^2 U^T \]
또는
\[ YY^T \mathbf{u}_i=\sigma_i^2 \mathbf{u}_i, \ \ \ i=1, ..., n \]
따라서 행렬 \(YY^T\)의 고유값은 \(\sigma_i^2\)이고 고유벡터는 \(\mathbf{u}_i\)가 된다. 특이값은 큰 수에서 작은 수의 순서로 정렬되어 있으므로 최적의 d차원 (\(d \lt n\)) 직교 좌표축 \(\mathbf{w}_i, \ i=1, ..., d\) 는 다음과 같이 선택하면 된다.
\[ \begin{align} W &= \begin{bmatrix} \mathbf{w}_1 & \mathbf{w}_2 & \cdots & \mathbf{w}_d \end{bmatrix} \\ \\ &= \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_d \end{bmatrix} = U_d \end{align} \]
그러면 좌표축 \(\mathbf{w}_i, \ i=1, ..., d \) 의 축성분은 다음식으로 계산된다.
\[ \mathbf{z}_i = U_d^T \left( \mathbf{x}^{(i) } - \mathbf{\mu} \right) \]
복원될 또는 투사된 데이터의 근사값 \(\hat{\mathbf{x}}^{(i)}\)는 다음과 같이 계산된다.
\[ \hat{\mathbf{x}}^{(i)} = \mathbf{\mu}+ U_d \mathbf{z}_i \]
또한 투사 오차는 다음과 같이 계산된다.
\[ \begin{align} J &= \sum_{i=1}^m \lVert \mathbf{y}^{(i)}- WW^T \mathbf{y}^{(i)} \rVert_2^2 \\ \\ &= trace \left[ YY^T \right] - trace \left[ W^T YY^T W \right]\\ \\ &= trace \left[ U\Sigma^2 U^T \right] - trace \left[ U_d^T U\Sigma^2 U^T U_d \right] \\ \\ &= \sum_{i=1}^r \sigma_i^2 -\sum_{i=1}^d \sigma_i^2 \\ \\ &= \sum_{i=d+1}^r \sigma_i^2 \end{align} \]
여기서 \(r\)은 평균점으로 조정된 스냅샷 행렬 \(Y \in \mathbb{R}^{n \times m}\)의 랭크(rank)다. 따라서 축소 차원 \(d\)를 \(d=r\)로 선택하면 투사 오차는 \(0\)이 된다.
일반적으로 축소 차원 \(d\)는 설계자가 미리 설정한 투사 오차 비율 \(\eta\)보다 작도록 다음과 같이 선정한다.
\[ \frac{ \sum_{i=d+1}^r \sigma_i^2 }{ \sum_{i=1}^r \sigma_i^2 } = 1 - \frac{ \sum_{i=1}^d \sigma_i^2 }{ \sum_{i=1}^r \sigma_i^2 } \le \eta \]
'유도항법제어 > 데이터기반제어' 카테고리의 다른 글
| [POD-2] 스냅샷 적합직교분해 (snapshot POD) (0) | 2021.03.01 |
|---|---|
| [POD-1] 고전 적합직교분해 (classical POD) (0) | 2021.02.28 |
| [PCA–4] PCA 예제: Eigenfaces (0) | 2021.02.24 |
| [PCA–3] 주성분 분석 (PCA) 특징 (0) | 2021.02.20 |
| [PCA–1] 주성분 분석 (PCA) (0) | 2021.02.18 |




댓글