다음과 같이 2차원 공간(평면)상에 표현된 데이터 \(\mathbf{x}^{(i)}, \ i=1,...,m\) 이 있다.
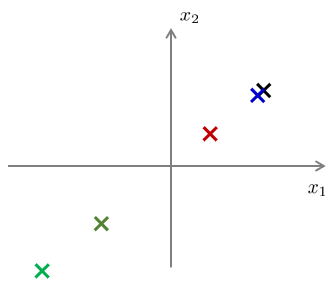
데이터를 연결해 보니 데이터가 모두 직선상에 있다는 것을 알게 됐다고 하자. 이 직선으로 표현된 축(성분)을 \(z_1\)으로 한다면 애초에 \(x_1\)과 \(x_2\)의 두 축(성분)으로 이루어진 2차원 공간상의 데이터를 \(z_1\)축으로 이루어진 1차원 공간상에 표현할 수 있었을 것이다.
이와 같이 고차원 데이터를 저차원 데이터로 표현하는 것을 차원 축소(dimensionality reduction)라고 한다.

만약 데이터가 일직선 상에 있지 않고 약간 어긋나 있다면 어떨까.

그렇다고 하더라도 데이터가 나타내는 정보의 일부분을 잃는 것을 감수할 수 있다면 원래의 데이터 \(\mathbf{x}^{(i)}\)를 한 개의 축 \(z_1\)상의 데이터 \(\hat{\mathbf{x}}^{(i)}\)로 근사적으로 표현할 수 있다 (\(\mathbb{R}^2 \to \mathbb{R}^1\)).
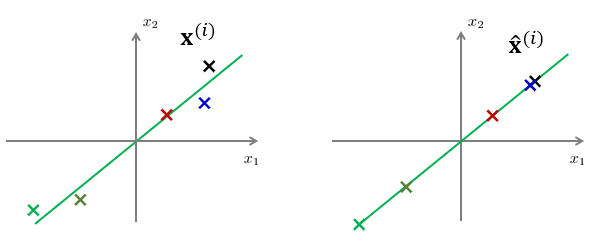
좌표상에서 데이터의 위치가 곧 데이터의 정보를 나타내므로 정보를 원래 모습 그대로 최대한 유지하려면(또는 정보 손실을 최소화하려면) 원래 데이터 \(\mathbf{x}^{(i)}\)와 근사화된 데이터 \(\hat{\mathbf{x}}^{(i)}\) 간의 거리 오차 \(\lVert \mathbf{x}^{(i)}-\hat{\mathbf{x}}^{(i)} \rVert_2\)를 최소화하면 될 것이다.
그렇다면 오차를 최소화하기 위해서는 좌표축의 방향(성분)은 어떻게 결정해야 할까. 우선 원래의 데이터를 어떤 좌표축에 투사시켰을 때 생기는 투사 오차(projection error)를 최소화하도록 좌표축을 정하면 될 것 같다.
투사(projection)란 좌표축 또는 좌표 평면과의 거리가 최소가 되도록 수직으로 비추는 것을 말한다.

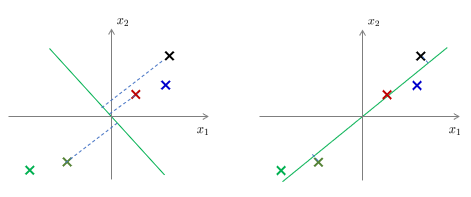
아래 그림에서 왼쪽 그림보다는 오른쪽 그림이 전체적인 투사 오차가 더 작도록 좌표축 방향을 결정한 것이다.
다음과 같이 3차원 공간상에 표현된 데이터 \(\mathbf{x}^{(i)}\)도 2차원 평면상의 직교 좌표축에 투사시켜서 차원을 축소할 수 있다 (\(\mathbb{R}^3 \to \mathbb{R}^2\)). 고차원 공간상의 데이터도 비슷한 방법으로 저차원 공간으로 차원을 축소할 수 있다 (\( \mathbb{R}^n \to \mathbb{R}^d \)).

이와 같이 데이터에서 가장 중요한 정보를 추출하고 이 정보를 '주성분' 이라고 하는 새로운 직교 변수 집합으로 차원을 축소하여 표현하는 해석 방법을 주성분 분석(PCA, principal component analysis)이라고 한다.
'유도항법제어 > 데이터기반제어' 카테고리의 다른 글
| [POD-2] 스냅샷 적합직교분해 (snapshot POD) (0) | 2021.03.01 |
|---|---|
| [POD-1] 고전 적합직교분해 (classical POD) (0) | 2021.02.28 |
| [PCA–4] PCA 예제: Eigenfaces (0) | 2021.02.24 |
| [PCA–3] 주성분 분석 (PCA) 특징 (0) | 2021.02.20 |
| [PCA–2] 주성분 분석 (PCA) 알고리즘 유도 (0) | 2021.02.19 |




댓글